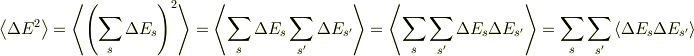2乗平均
2乗平均
トビラ.. さんの書込 (2009/12/17(Thu) 23:04)
こんばんわ 2乗平均(分散?)についてよくわからないんですが,僕の持っている本では,この2乗平均を次のように計算しています. まず,2乗平均を次のように定義します.
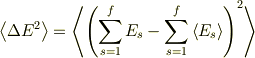
ここで,  は平均を意味します.
この計算をこの本では,この後,
は平均を意味します.
この計算をこの本では,この後,
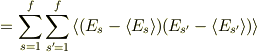
となっているんですが,どうやってシグマを括弧の外に出したのかよくわかりません.シグマが括弧の外か内にあるかで,意味は変わってきますよね? わからず困ってます.どうか,アドバイスお願いします.
Re: 2乗平均
トビラ.. さんのレス (2009/12/18(Fri) 00:39)
yamaさんありがとうございます. なるほど!変な解釈をしていました.つまり,
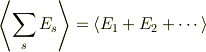
と
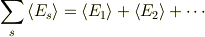
はイコールなんですね!総和の平均が前者で,平均の総和は後者ですよね?僕には後者の方が前者より大きい値をもつように感じていたんですが,なぜかというと,前者は足した後,足した数で割ったりして平均を求めるのかと思っていたけども,そうじゃなくて,足した値(計算した後)での平均値という意味なんですね.(説明下手でごめんなさい)なるほど,感動しました.どうもありがとうございます.
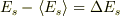 と置くと
と置くと