３質点の運動エネルギーの和

３質点の運動エネルギーの和

qwer さんの書込 (2009/12/05(Sat) 23:04)

質量m_1,m_2,m_3の３質点の位置ベクトルをr_1,r_2,r_3とし，R,r,sという３つのベクトルを R = (m_1r_1+m_2r_2+m_3r_3)/(m_1+m_2+m_3)

r = r_1 - r_2

s = r_3 - (m_1r_1+m_2r_2)/(m_1+m_2)

とする．このとき，３質点の運動エネルギーの和は，

T = (m_1+m_2+m_3)/2 * R[]^2 + m_1m_2/{2(m_1+m_2)} * r[]^2 + m_3(m_1+m_2)/{2(m_1+m_2+m_3)} * s[]^2

とかける．

（R[],r[],s[]の[]は時間微分せよという意味で使いました．）

換算質量という量に留意し，右辺の３つの項の意味を物理的に解釈せよ．

という問題なのですが，

第１項は，３質点の重心の運動エネルギー 第２項は，質量m_1,m_2の質点を一体（Aとする）とみたときのAの運動エネルギー 第３項は，質量m_1,m_2,m_3の質点を一体（Bとする）とみたときのBの運動エネルギー

を表している．

という答えで，よろしいでしょうか．

Re: ３質点の運動エネルギーの和

Yokkun さんのレス (2009/12/05(Sat) 23:56)

まず，２質点の場合について理解を深められるのがよいと思います．

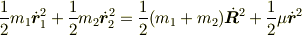
\frac{1}{2}m_1{\dot{\bm r}_1}^2 + \frac{1}{2}m_2{\dot{\bm r}_2}^2 = \frac{1}{2}(m_1+m_2){\dot{\bm R}}^2 + \frac{1}{2}\mu \dot{\bm r}^2

ここで，

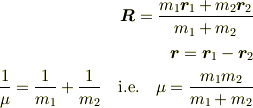
{\bm R} = \frac{m_1 {\bm r}_1 + m_2 {\bm r}_2}{m_1 + m_2}\\{\bm r} = {\bm r}_1 - {\bm r}_2\\\frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2} \quad {\rm i.e.} \quad \mu = \frac{m_1m_2}{m_1+m_2}

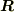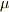{\bm R} は重心の位置ベクトル， {\bm r} は相対位置ベクトル， \mu は換算質量です．

系の運動エネルギーを書き換えた右辺の第１項は，重心運動のエネルギー（系の並進運動のエネルギー），第２項は相対運動のエネルギーにあたります．

以上を理解されれば，３質点の場合もおのずと明らかではないでしょうか？

Re: ３質点の運動エネルギーの和

qwer さんのレス (2009/12/06(Sun) 00:58)

では， 第１項３質点の重心の運動エネルギー 第２項質量m_2の質点から質量m_1の質点をみたときの，相対運動エネルギー 第３項質量m_1,m_2の重心から質量m_3の質点をみたときの，相対運動エネルギー

をそれぞれ表している，ということでいいですか？

Re: ３質点の運動エネルギーの和

Yokkun さんのレス (2009/12/06(Sun) 01:48)

概ねよいと思います．が，

第２項は，質量m_1，m_2の２質点の相対運動のエネルギー 第３項は，質量m_1，m_2の２質点の重心と質量m_3の質点の相対運動のエネルギー

といっていいでしょう．変位は相対変位になっていますが，換算質量を用いなければならないのですから，〜から見た・・・というのは妥当でない気がします．たとえば第２項は，相互の重心から見た２質点の運動エネルギーになるのです．

Re: ３質点の運動エネルギーの和

qwer さんのレス (2009/12/06(Sun) 02:31)

＞たとえば第２項は，相互の重心から見た２質点の運動エネルギーになるのです．

なぜ，重心から見たものになるのでしょうか？ rは，質量m_2の質点から質量m_1の質点をみたときの位置ベクトルを表しているんですよね？なぜ，重心が出て来るのでしょうか？

あと，そもそも換算質量とはなんなのでしょうか？単に，こうおけばすっきりするから，便宜上導入しただけのものなのでしょうか？

Re: ３質点の運動エネルギーの和

Yokkun さんのレス (2009/12/06(Sun) 09:16)

簡単な系を考えてみましょう．

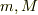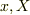質量 m,M の質点が自然長 L ，ばね定数 k のばねの両端についていて，なめらかな水平面をすべっているとします．それぞれの座標を x,X とすると運動方程式は，

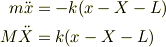
m\ddot{x} &= -k(x-X-L)\\M\ddot{X} &= k(x-X-L)

となります．２つの座標が混在した連立微分方程式になっています．両辺を質量で割って辺々引くと，

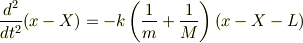
\frac{d^2}{dt^2}(x-X) = -k\left(\frac{1}{m}+\frac{1}{M}\right)(x-X-L)

これが相対座標の運動方程式ですね？この右辺の第２因子の逆数が換算質量になります．なお，重心運動の方程式は，辺々加えて

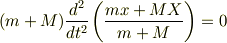
(m+M)\frac{d^2}{dt^2}\left(\frac{mx+MX}{m+M}\right) = 0

を得ます．

一方，はじめから重心とともに動く座標系で運動方程式をたててみましょう．

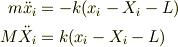
m\ddot{x}_i &= -k(x_i - X_i - L)\\M\ddot{X}_i &= k(x_i - X_i - L)

ここで，質量中心系（重心系，慣性中心系，C系などとも呼ぶ）における両者の座標を実験室系のものに書き戻すと，

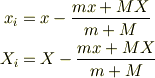
x_i &= x - \frac{mx + MX}{m+M}\\X_i &= X - \frac{mx + MX}{m+M}

これらを代入すると，２つの運動方程式がいずれも相対運動の方程式になることがわかります．

ですから，相対運動の方程式は質量中心系でみた運動方程式なのです．これを相対変位で表現すると最初につくった形になるわけですが，その副作用が換算質量になったと理解できそうですね．換算質量は，本来何の運動実体（？）も対象としていない仮想上の概念ですから，いわば形式上の便宜といえるでしょう．でも，相対座標を使う限りいつでも換算質量を使えば運動方程式やエネルギー積分を簡単に書けるので，とても便利なものであるといえます．

相対座標の運動方程式は，qwerさんがおっしゃるとおり，「質量m_2の質点から質量m_1の質点をみたときの」運動方程式とみることももちろんできます．先に「〜から見た・・・というのは妥当でない」といった私の表現はちょっと誤解を招く勇み足でした．それがわかるように書き直せば，（ M からみた m の運動方程式)

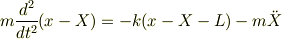
m\frac{d^2}{dt^2}(x-X) = -k(x-X-L) - m \ddot{X}

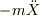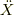両辺に -m\ddot{X} を付け加えただけですが，右辺第２項は M が加速度運動しているために， m には慣性力が働くように見えるということを示しています．これに M の運動方程式から \ddot{X} を代入してやれば，同じ結果を得ます．

Re: ３質点の運動エネルギーの和

qwer さんのレス (2009/12/08(Tue) 23:10)

遅れてすみません．

こんなに丁寧に回答してくれるとは思ってもいませんでした． 非常に参考になりました．

ありがとうございました．