粒子(質点)系
粒子(質点)系
ソロ さんの書込 (2009/12/05(Sat) 16:15)
N粒子系における全力学的エネルギーの保存について考える.
粒子 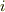 の運動方程式は,内力を
の運動方程式は,内力を 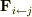 ,外力を
,外力を 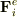 とすると,
(内力と外力はいずれも保存力とする.)
とすると,
(内力と外力はいずれも保存力とする.)
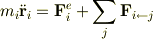
(  ,
, 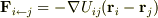 ,
, 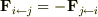 )
)
このとき全力学的エネルギー  は,
は,
![E = \sum^{N}_{i=1}\Big[\frac{1}{2}m_i \dot{{\bf r}}^2_i + U_i ({\bf r}_i)\Big] + \frac{1}{2}\sum^{N}_{i=1}\sum^{N}_{j=1}U_{ij}({\bf r}_i - {\bf r}_j)](http://hooktail.maxwell.jp/bbslog/d42f5219e6b96a5c75253a0885a110a2.png)
今,2粒子系 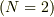 を考えると,
を考えると,
![E_2 = \sum^{2}_{i=1}\Big[\frac{1}{2}m_i \dot{{\bf r}}^2_i + U_i ({\bf r}_i)\Big] + \frac{1}{2}\sum^{2}_{i=1}\sum^{2}_{j=1}U_{ij}({\bf r}_i - {\bf r}_j)](http://hooktail.maxwell.jp/bbslog/30456a7e16e37fb5d1d8152081ae4fc0.png)
整理すると( 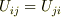 ,
, 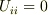 より)
より)
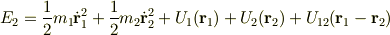
この 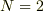 のとき,
のとき,  が一定となる事を示したいのですが,ここからどうしたらいいのか分かりません.
よろしくお願いします.
が一定となる事を示したいのですが,ここからどうしたらいいのか分かりません.
よろしくお願いします.
Re: 粒子(質点)系
Yokkun さんのレス (2009/12/05(Sat) 17:37)
時間微分をとって,ゼロになることを示せばよいのではないでしょうか?
運動方程式の座標積分がエネルギー原理(力学的エネルギー保存)ですから, 運動方程式を使えばよいのだと思います.