ｇｇ さんの書込 (2009/12/05(Sat) 11:09)

非線形最小二乗計算を制約条件付(可変パラメータの上限値，下限値を指定する)で行いたくて，このような計算をしてくれるCのライブラリを探しています．よいライブラリがあったら教えて下さい．

yt さんのレス (2009/12/05(Sat) 16:34)

ｇｇ さん，はじめまして．

使ったことはありませんが，商用のライブラリなら，NAG や IMSL で望まれている計算が可能だと思います． フリーの場合は，GSL(GNU Scientific Library) などは如何でしょうか． GSLは「物理のかぎしっぽ」の計算物理学の項目でも紹介されています．

■GSL Windows版 2009年12月現在，このサイト( http://david.geldreich.free.fr/dev.html )にて入手可能です． 通常は，binary版で大丈夫かと思います．(挙動がおかしい/性能云々の場合は，source版を拾ってきてライブラリをコンパイルする事もできます)

私の環境( Visual C++ 2008 Express Edition ) でプログラムをコンパイルする際は， includeパスに「〜gslinclude」 libraryパスに「〜gsllib」 を通し，リンカの追加依存ファイルに，「cblas.lib gsl.lib」 を追加しておきます．(Debugモードの時は, 「cblas_d.lib gsl_d.lib」) これだけでOKでした．

■GSL Linux版 yum なり apt-get で簡単に導入可能だと思います．或いは(以下省略)

■GSLマニュアル ・マニュアル日本語版(PDF): 461頁に 「第37章 非線形最小二乗近似」 があります

• http://www.cbrc.jp/~tominaga/translations/gsl/gsl-1.11/gsl11.pdf

・マニュアル英語版(HTML)： Nonlinear Least-Squares Fitting

• http://www.gnu.org/software/gsl/manual/html_node/Example-programs-for-Nonlinear-Least_002dSquares-Fitting.html

■マニュアルで紹介されているサンプルプログラム 前半: expfit.c (VC++では拡張子を.h に変えた方が面倒な事になりません) モデルとなる関数とパラメータ毎の偏微分関数を準備しておきます．

後半: main.cpp 適当なテスト用データ作った後，モデル関数とパラメータ初期推定値etc.を指定し，ループ処理に入ります，適当な収束条件を満たせば終了になります．

■制約条件 >制約条件付(可変パラメータの上限値，下限値を指定する)

このような場合， パラメータが制約外に出る時はモデル関数(例. 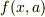)の値を遠くに振ってしまえば良いのではないでしょうか？ 偏微分関数の指定も必要なので，不連続に振ると上手くいかないかもしれません．

なので，以下のような感じで制約に少しだけ遊びを持たせては如何でしょうか． パラメータ の上限 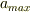を指定する場合 単純に，

或いは，境界で滑らかな，

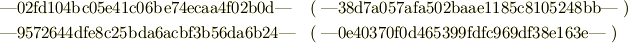
制約条件を課すのは計算の収束を早めるためのガイド役として有効かと思います． ただし，問題にもよりますが，フィットした結果得られるパラメータが制約境界に張り付いているような場合は，指定したモデルがあまり相応しくないのかも知れません． すみません．あまり詳しくはないので，これ以上の引き出しは空っぽです．．．

ｇｇ さんのレス (2009/12/07(Mon) 20:39)

回答をありがとうございます！

現在，Linuxでminpackを使ってCで最小二乗計算をやってみています． GSLというのがあるのですね．便利そうです．

ただ，どちらを使っても，制約条件無しの計算しかやってくれないようなので，教えて頂いたような方法でユーザーが制約条件を付けるしかないようですね．． パラメータの値が制限値を超えたときのモデル関数の関数形の決め方には常套手段があるのでしょうか．また，どの関数を使うかは試行錯誤で決めるしかないのでしょうか．何らかの指標があるのでしょうか．

ところで，ネットで検索していたら，下記のようなものを見つけました．

• http://www.mlab.ice.uec.ac.jp/~ej-sib/numerical/numerical_levmar.html
• http://www.ics.forth.gr/~lourakis/levmar/

良くわからないのですが，これは質問させていただいたような計算を行ってくれるのでしょうか．

また，Matlabの最小二乗計算には制約条件を付けることが出来るようなのですが，Matlabで使われているライブラリと同じものをCで使うことは出来ないのでしょうか．

yt さんのレス (2009/12/08(Tue) 00:31)

先程 levmar ダウンロードして試してみました． コンパクトなのに中々面白そうなライブラリですね． ■Makefile 環境によって変わると思いますが，私の場合(Linux:FedoraCore10) は以下の箇所を変更しました． LAPACKLIBS_PATH=/usr/lib LAPACKLIBS=-llapack -lblas -lgfortran

■制約条件 制約条件については，dlevmar_bc_derまたは，dlevmar_bc_dif で対応可能のようです．bc は box-constrained の事ですね．デモプログラムに指定例が幾つかありました． dlevmar_der/dif に， lb (LowerBound), ub (UpperBound) の引数が追加されているだけです． ｇｇさんが挙げられていた日本語のサイトには，dlevmar_der は MINPACKの lmder に相当するとあるので，minpack に慣れているｇｇさんなら使いこなせるのではないでしょうか？ 私は，デモプログラムをいじって，まだほんの上っ面に触れただけです． 各デモ(problem=0〜20)についても解説できるレベルにありません．．．

■デモプログラム1: lmdemo.c デモ番号をコマンドの引数で指定できるように以下の変更をしました．(problem毎にコンパイルするのが面倒) line.174: int main(int argc, char* argv[]) line.821: problem= atoi(argv[1]); line.826: // 4; // Meyer's (reformulated) problem

■デモプログラム2: expfit.c こちらは make では生成されません．(例: gcc -o expfit expfit.c -I. -L. -llevmar -llapack -lblas -lgfortran -lm ) ・オリジナルの実行結果: Best fit parameters: 4.95717 0.09764465 0.9819239

・制約条件付きに変更: line.25: #include <float.h> //DBL_MAXの定義あり... line.116: double lb[3], ub[3]; lb[0]=lb[1]=lb[2]= -DBL_MAX; ub[0]=ub[1]=ub[2]= DBL_MAX; ub[0]=4.5; ret=dlevmar_bc_der(expfunc, jacexpfunc, p, x, m, n, lb, ub, 1000, opts, info, NULL, NULL, NULL);

・制約条件付き実行結果: Best fit parameters: 4.5 0.09402639 0.9876752 (上限に張り付いてますｗ)

こんな感じでした．

■>パラメータの値が制限値を超えたときのモデル関数の関数形の決め方には常套手段があるのでしょうか． すみません特に常套の手段は知らないです． 先のレスで挙げた方法は，パラメータがおかしな極小点に転んで収束しないように，大昔そんなやり方でのりきった覚えがあります． (確かFortranのライブラリでしたが，もう忘れてしまいました) 今思うと，ブラックボックスなライブラリに対応するためだけの小手先の手段のようにも思います． 仮に自分で一から実装するのなら，境界を越えそうなステップを普通に禁止するだけっぽく思えるので．(禁止ってだけじゃなく，その際どっちに進むかの実装が面倒そうですが)

■Matlab Matlabは使ったことがありません，C言語との連携についても知りません．．． どなたか，フォローをお願いします．

■追信 逆方向になりますが， Octave(Matlabでも同様のはず) に levmar の機能が追加できました．

levmar-2.5/matlab にて octaveを起動．．． octave:1> mex -DHAVE_LAPACK -I.. -L.. levmar.c -llevmar -lblas -llapack -lgfortran このコンパイルモドキで「levmar.mex」ができました． .mex ファイルはライブラリファイルのようなものだと思います．

octave:2> help levmar ... dlevmar_bc_der 相当の作業も可能なようです．

この方向でも良いのであれば， これ(levmar.c)を参考にして，モデル関数とヤコビアンも C言語＋αで用意して云々．．．んー，これだけを見ても判りにくいです． 例えば，こちらの方のサイト( http://www.edu.cs.kobe-u.ac.jp/~mori/Matlab/mexmemo.html )などが参考になるかも知れません．