お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
鐘蔵 さんの書込 (2009/11/27(Fri) 12:21)
こんにちは, お寺の鐘を指で鳴らす場合,指1本でうまくつくと小さく低い音で鳴り始めます.お寺の鐘の固有振動数は数百ヘルツくらいですが,この固有振動数の整数分の一のスピードでつけば振動が成長します.この辺りを式で表すと,どのような式になるのでしょうか?強制振動の式が絡むような気がするのですが,整数分の一が必要なことが式でわかりません.
Re: お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
Yokkun さんのレス (2009/11/27(Fri) 19:18)
こんにちは.
難しいことはよくわかりませんが,固有振動数というのは鐘が振動しやすい振動の速さを,1秒間当たりの振動回数で表したものですよね.とすれば,n分の1でつっつくということは,鐘がn回振動するごとにつっついてやるということです.ぶらんこを何回かに1回おしてやるのと同じです.そんなことはわかっている上でのご質問ならば,ごめんなさい.
Re: お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
mNeji さんのレス (2009/11/28(Sat) 18:37)
鐘蔵さん,おもしろいお話と思います.
もし,実際に試されたとするならば,もうすこし実験内容を詳しく記述して頂ければと思います.
なお,お寺の鐘は「ゴ〜〜ン〜ン」といった感じで,「100Hz以下ぐらいの振動」と,「数Hzぐらいのうなり」とから成り立つようだと思うのですが,如何でしょうかね.
Re: お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
yama さんのレス (2009/11/28(Sat) 21:53)
確かに固有振動数の整数分の一のスピードでつくことができれば振動が成長すると思いますが,指でつく場合は正確に固有振動数の整数分の一を保つのは不可能ではないでしょうか. 例えば固有振動数を100Hzとして,その50分の1の回数でつくとすると0.50秒毎につくことになりますが,これを少しずらして0.505秒毎についた場合は振動は成長しません. したがって指で鐘をつく時間間隔を0.005秒以下の精度で一定に保たないといけないし,指が鐘に接触している時間も0.005秒以下にしないといけませんが,それはほとんど不可能であるように思われます.
Re: お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
yt さんのレス (2009/11/29(Sun) 13:07)
鐘蔵さん,こんにちは. 強制振動の運動方程式がお望みのようなので書き下してみました. 多少説明が足りない箇所も式自身が語ってくれる事を期待します.
![\ddot{x} = -\omega_0^2 \, x - \alpha \dot{x} + f(t) \hspace{3em} [\;\rm{Laplace\; transform}\downarrow\;]](http://hooktail.maxwell.jp/bbslog/1b52f7d08fcce7a75a61262bd841a14b.png)
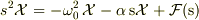
![\mathcal{X}(s) = \frac{1}{ \left(s + \frac{\alpha}{2} \right)^2 + \left( \omega_0^2 - \frac{\alpha^2}{4}\right) } \, \mathcal{F}(\rm{s}) \hspace{3em} \left[ \;\omega_1 \stackrel{\scriptsize def}{=} \sqrt{\omega_0^2 - \frac{\alpha^2}{4}}\; \right] \hspace{2em} [\;\rm{inverse\; Laplace\; transform}\downarrow\;]](http://hooktail.maxwell.jp/bbslog/98dbbbf1bd69586e246d621e1068aca4.png)
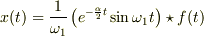
![= \frac{1}{\omega_1} \int_0^t \left[ e^{-\frac{\alpha}{2}(t-\tau)} \sin\omega_1(t-\tau) \right] f(\tau) \,d\tau](http://hooktail.maxwell.jp/bbslog/851aa2e79600f8cd9c0cf770107e18dd.png)
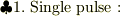
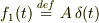
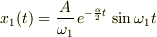
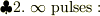
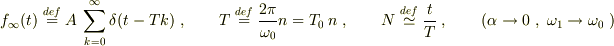
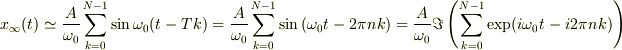
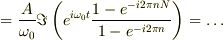
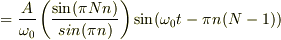
![\approx \frac{A}{\omega_0} N \sin(\omega_0 t) = \frac{A\,t}{2\pi n} \sin(\omega_0 t) \hspace{2em} \left[\rm{\;if\;n\;is\;Natural\;Number\pm\delta n\;\;\;(tolerance\!:\,\delta n \sim \frac{1}{N})\;} \right]](http://hooktail.maxwell.jp/bbslog/d1b1154b633facc80822a550a9f26a41.png)
まず最初の式の右辺は,振動項(固有角振動数 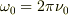 ),減衰項(振動エネルギーが熱や音波など変換されて散逸する現象を考慮), 強制力項(時間の関数
),減衰項(振動エネルギーが熱や音波など変換されて散逸する現象を考慮), 強制力項(時間の関数 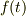 )からなっています.
そして,
)からなっています.
そして, 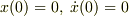 の初期条件でラプラス変換,式変形,ラプラス逆変換といった手順で,変位
の初期条件でラプラス変換,式変形,ラプラス逆変換といった手順で,変位 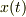 の解を求めています.途中の星印
の解を求めています.途中の星印  は畳み込み積分を表しています.途中計算は無視してもいいと思います.
とにかく得られた積分表示から,各時刻
は畳み込み積分を表しています.途中計算は無視してもいいと思います.
とにかく得られた積分表示から,各時刻  の衝撃
の衝撃 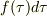 が,応答関数を通じて時刻
が,応答関数を通じて時刻  に伝わり,それぞれの応答が積み重なっている事が判ります.
に伝わり,それぞれの応答が積み重なっている事が判ります.
さてここで問題になるのは,強制力項 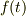 にどんな関数を当てはめてみるかなんですが,
にどんな関数を当てはめてみるかなんですが, 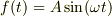 といった正弦波の振動で揺らしても固有振動数近傍以外の振動数では共振しません. 一瞬,Yokkunさんの挙げたブランコの例による直感とは異なるように感じるかも知れません.これは正弦波は純粋にその振動数成分しか持たない事によるものです.
ですが,一般の周期関数はその周期の整数分の1(基本振動数の整数倍)の成分が適当な比率で合わさって出来ています.条件が合えば,基本振動数より高い振動成分による共振(共鳴)を起こす事が可能です.
といった正弦波の振動で揺らしても固有振動数近傍以外の振動数では共振しません. 一瞬,Yokkunさんの挙げたブランコの例による直感とは異なるように感じるかも知れません.これは正弦波は純粋にその振動数成分しか持たない事によるものです.
ですが,一般の周期関数はその周期の整数分の1(基本振動数の整数倍)の成分が適当な比率で合わさって出来ています.条件が合えば,基本振動数より高い振動成分による共振(共鳴)を起こす事が可能です.
具体的な周期関数を考慮する前に,『 Single pulse 』の解では,コツンと一突きした場合の強制力をデルタ関数で近似した時の現象を見ています. デルタ関数は全ての振動数成分を満遍なく持つので,鐘の固有振動数に合った成分が振動を励起するのです.減衰項により固有振動数が僅かにずれ,同じく減衰項によって実質有限時間で音が鳴り止む事が読み取れます.
周期関数の例としての『 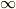 pulses 』の解では,周期
pulses 』の解では,周期 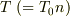 の時間間隔でコツコツ突き続ける場合の現象を見ています. 簡単のため減衰項は無視しています.
nが整数の時に振幅が成長するのは予想どおりですが,nには極わずかな許容範囲(
の時間間隔でコツコツ突き続ける場合の現象を見ています. 簡単のため減衰項は無視しています.
nが整数の時に振幅が成長するのは予想どおりですが,nには極わずかな許容範囲( 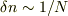 )がある事がわかります.
つまりN回連続で突き続ける間,振幅を成長させるには
)がある事がわかります.
つまりN回連続で突き続ける間,振幅を成長させるには 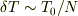 程度の周期誤差が許されます.これが崩れると変動がどんどん相殺されてしまい,精々2,3回程度小突いた分 (正確には周期誤差が許容範囲に納まってくれる程度の直近の数回分) の振幅しか得られません.
程度の周期誤差が許されます.これが崩れると変動がどんどん相殺されてしまい,精々2,3回程度小突いた分 (正確には周期誤差が許容範囲に納まってくれる程度の直近の数回分) の振幅しか得られません.
例えば,共振(共鳴)を期待して固有振動数 100Hzの鐘を(100, 50, 25Hz...で)100回突く場合は,周期誤差は 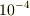 秒程度しか許されません.
人力では無理でしょうが,機械でやるとすれば,鳴っている音の周波数を元にフィードバックをかけてやれば何とかなる(=低周波の刺激で高周波共振を引き起こす)かも知れません.
ただし長時間では減衰項が無視できず,大振幅ではより高次の項が無視できなくなってきて単純なモデルでは表せなくなってきます.どれだけ正確に突き続けても程々の振幅で高止まりするように思います.
声の音波でガラスのコップを割れる人が存在するそうなので,材質や形状によっては破壊レベルまで振幅を成長させられるかと思います.お寺の鐘なら壊さないまでも,きっとそれなりの音量まで鳴らせられるかと思います.
秒程度しか許されません.
人力では無理でしょうが,機械でやるとすれば,鳴っている音の周波数を元にフィードバックをかけてやれば何とかなる(=低周波の刺激で高周波共振を引き起こす)かも知れません.
ただし長時間では減衰項が無視できず,大振幅ではより高次の項が無視できなくなってきて単純なモデルでは表せなくなってきます.どれだけ正確に突き続けても程々の振幅で高止まりするように思います.
声の音波でガラスのコップを割れる人が存在するそうなので,材質や形状によっては破壊レベルまで振幅を成長させられるかと思います.お寺の鐘なら壊さないまでも,きっとそれなりの音量まで鳴らせられるかと思います.
Re: お寺の鐘を整数分の一のスピードでついて鳴らす場合の式について
yama さんのレス (2009/12/01(Tue) 10:22)
鐘が完全弾性体であったとしても,鐘を打つ仕事が音として空気中に放射されるエネルギーに等しくなったところで振幅の増加は止まるでしょうね.