質点系の力学
質点系の力学
tt さんの書込 (2009/11/26(Thu) 16:38)
一様な重力のもと(重力加速度をgとする)で,下方にロケットに対して 相対速度uで単位時間に質量μの割合でガスを噴射しながら鉛直上方に進む ロケットがある.ロケットの初めの質量をm0,初速度をゼロとすると,時刻tの ロケットの速度と上昇高度はいくらか.
運動量と力積の関係を使って解く問題ですが,わかりません. 全然わからないので,お願いします.
Re: 質点系の力学
yt さんのレス (2009/11/27(Fri) 01:47)
微小時間  の間に,重力による力積
の間に,重力による力積 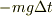 が全系(ロケット+燃料)の運動量変化
が全系(ロケット+燃料)の運動量変化 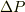 を引き起こします.
また,
を引き起こします.
また, 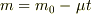 に注意すると
,
に注意すると
,

![\left[\, m'v' + (v-u)\mu\Delta t \,\right] - mv = - mg\Delta t](http://hooktail.maxwell.jp/bbslog/34f3c8835766e0df54587744268aee84.png)
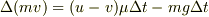
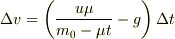
後は頑張って積分して下さい.
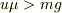 の条件が満たされるまでは上昇を開始しない事に注意.
の条件が満たされるまでは上昇を開始しない事に注意.
Re: 質点系の力学
mNeji さんのレス (2009/11/28(Sat) 03:27)
ttさん,運動方程式を立てるところを差分的に考えて見ます.
原点Oから垂直にX軸を考えて,ロケットの位置座標 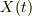 とします.ロケットの質量
とします.ロケットの質量 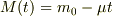 ,速度
,速度 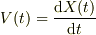 とします.
とします.
ここで,時刻  と時刻
と時刻 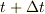 との間で,
質量:
との間で,
質量: 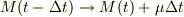 速度:
速度: 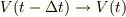 と離散的に変化したとします.
と離散的に変化したとします.
<pre>
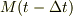
 -------->
■■■■■■■
■■■■■■■
■■■■■■■
-------->
■■■■■■■
■■■■■■■
■■■■■■■
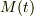
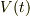 -------------->
■■■■■■■
-------------->
■■■■■■■
■ ■■■■■■
■■■■■■■
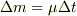
 </pre>
</pre>
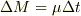 は,燃焼して,ロケットから噴出したガス部分ですが,飛び出すまでに,ロケットに力
は,燃焼して,ロケットから噴出したガス部分ですが,飛び出すまでに,ロケットに力 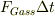 を与えます.
を与えます.
従って,ロケットと,ガス部分の運動量変化;
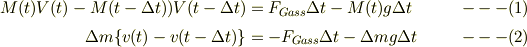
式(2)に相対速度の変化を用い,二次の微小変化を無視して,
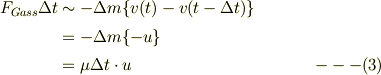
を得る.
また,式(1)の左辺を整理すると,
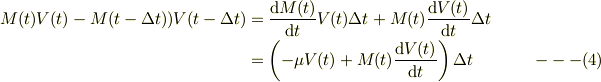
となるので,式(1)に,式(3),(4)を代入して,
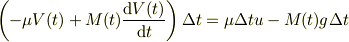
整理して,
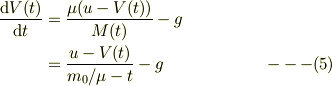
Re: 質点系の力学
yt さんのレス (2009/11/28(Sat) 09:13)
mNejiさん
ロケットの推力 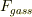 にも言及していて,より丁寧な解説だと思います.ですが(5)で
にも言及していて,より丁寧な解説だと思います.ですが(5)で  が微弱,
が微弱, 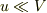 の状況を想像してみて下さい.変です...
の状況を想像してみて下さい.変です...
微小時間  の間
・ロケット部分(質量
の間
・ロケット部分(質量 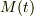 )
・噴出ガス部分(質量
)
・噴出ガス部分(質量 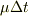 )
2つを分けて運動を考察しているので(
)
2つを分けて運動を考察しているので( 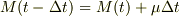 ),式(1)での質量は終始
),式(1)での質量は終始 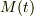 のままでよいはずです.
のままでよいはずです.
Re: 質点系の力学
mNeji さんのレス (2009/11/28(Sat) 18:30)
ytさん,
>ですが(5)で  が微弱,
が微弱, 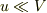 の状況を想像してみて下さい.変です...
の状況を想像してみて下さい.変です...
昨晩は眠たかったので検算はしていませんでした.今日も,いま拝見したのでこれから考える所です.
でも,「  が微弱」どころか,ゼロにして考えても論議は出来なくてはいけませんね.
が微弱」どころか,ゼロにして考えても論議は出来なくてはいけませんね.
「 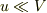 の状況を想像」は可能なんでしょうか?私は「噴射ガスの相対速度よりもロケットが速く飛べる」とは知りませんでした.
の状況を想像」は可能なんでしょうか?私は「噴射ガスの相対速度よりもロケットが速く飛べる」とは知りませんでした.
>式(1)での質量は終始 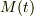 のままでよいはずです.
のままでよいはずです.
ロケットの運動量を考えているのですから, 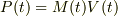 を基に,ロケットの運動方程式を立てるのは自然だと思います.
を基に,ロケットの運動方程式を立てるのは自然だと思います.
ただ,微小時間の中で,ロケットから噴出したガスとの相互作用を考えるには,其のガス部分の運動方程式を別途つくり,相互作用の力は,お互いに「作用・反作用の法則」に従う事を明示的に使うべきだと思います.
取り急ぎ,ご返答とさせて戴きます.
Re: 質点系の力学
mNeji さんのレス (2009/11/29(Sun) 01:16)
ytさん,見直しました.
>式(1)での質量は終始 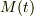 のままでよいはずです.
のままでよいはずです.
この部分はお説の通りで正しいと思いました.自分でも「質量: 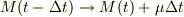 」と書いた様に,二つの部分に分割し,それぞれの運動を考察するという立場なので,式(1)は,
従って,ロケットと,ガス部分の運動量変化;
」と書いた様に,二つの部分に分割し,それぞれの運動を考察するという立場なので,式(1)は,
従って,ロケットと,ガス部分の運動量変化;
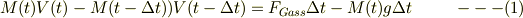
では無くて,
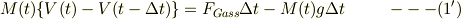
とするべきですね.関連して,式(5)は;
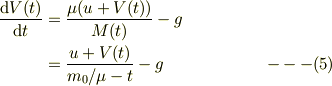
下記に変更となります.
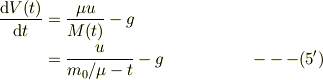
やや風邪気味なので,論議はここまでとさせて戴きます.
Re: 質点系の力学
yt さんのレス (2009/11/29(Sun) 15:18)
mNejiさん,こんにちは. 風邪気味の処,申し訳ありません.こちらの説明が足らなかった部分を少しだけ補足させてください.
> 「 |c1515276dec695ca0ad0b245ef4db3f8| の状況を想像」は可能なんでしょうか
はい,最後の式の段階では,初期条件 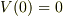 をまだ使っていないので好きな速度を当てはめて良いのです.
だから,V(0)=0 から開始して「噴射ガスの相対速度よりもロケットが速く飛べる」のかどうかの知識もここでは不要なのです.(質量の大半が燃料でロケットの機体が軽ければ,それが有り得るというのは積分した後で判ります)
イメージするなら十分な高高度(gが微小)でブースーターロケットを切り離した直後の宇宙船(Vが大)などがちょうど良いと思います.
重力圏を突破しているなら u = 0 で考えたって良いのです.宇宙船本体の燃料は,姿勢制御用と遠くの星に着陸するときの減速用に使うだけかも知れません.
「変です...」の箇所は,外力(Mg)が無視できるほど微小なのに,減速(加速度の値が負)される,しかも勢いがついている程ブレーキがかかる,そんな状況は物理的な直感に反する,(直感がいつも正しいとは限らないのですが) たぶん計算が間違っているのだろうといった意味で書きました.
をまだ使っていないので好きな速度を当てはめて良いのです.
だから,V(0)=0 から開始して「噴射ガスの相対速度よりもロケットが速く飛べる」のかどうかの知識もここでは不要なのです.(質量の大半が燃料でロケットの機体が軽ければ,それが有り得るというのは積分した後で判ります)
イメージするなら十分な高高度(gが微小)でブースーターロケットを切り離した直後の宇宙船(Vが大)などがちょうど良いと思います.
重力圏を突破しているなら u = 0 で考えたって良いのです.宇宙船本体の燃料は,姿勢制御用と遠くの星に着陸するときの減速用に使うだけかも知れません.
「変です...」の箇所は,外力(Mg)が無視できるほど微小なのに,減速(加速度の値が負)される,しかも勢いがついている程ブレーキがかかる,そんな状況は物理的な直感に反する,(直感がいつも正しいとは限らないのですが) たぶん計算が間違っているのだろうといった意味で書きました.
>...相互作用の力は,お互いに「作用・反作用の法則」に従う事を明示的に使うべきだと思います.
これにも一言.
「作用・反作用の法則」が成り立っているからこそ,2体に分けて考えようが全体で考えようが,(問題として相互作用の力の式が要求されていない限りは)どちらでも構わないのです.
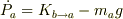
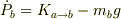
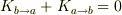 なので,
なので, 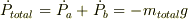 です.
です.
そして常に相互作用の力 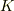 が書き下せるとは限らない事を付け加えておきます.その一例として原子核のγ崩壊をとりあげてみます.
高いエネルギー状態にある,原子核
が書き下せるとは限らない事を付け加えておきます.その一例として原子核のγ崩壊をとりあげてみます.
高いエネルギー状態にある,原子核 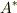 が低エネルギー状態
が低エネルギー状態 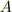 に遷移する際に,光子
に遷移する際に,光子 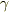 を放出する反応は,
を放出する反応は,
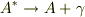 と書けます.量子力学的な反応とはいえ反応の前後で運動量とエネルギーが保存している点は,通常の力学と同じです.
ですがロケットの場合と異なるのは,
と書けます.量子力学的な反応とはいえ反応の前後で運動量とエネルギーが保存している点は,通常の力学と同じです.
ですがロケットの場合と異なるのは, 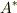 の中に内在していた
の中に内在していた 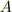 と
と 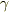 が相互作用の力で押し合って分裂するといったイメージで考えたりはしない点です.
左辺の状態から瞬間的に(各粒子それぞれ特定の運動量とエネルギーを持った)右辺の状態に遷移すると考えるのが一般的です.
だから力学の式は,
が相互作用の力で押し合って分裂するといったイメージで考えたりはしない点です.
左辺の状態から瞬間的に(各粒子それぞれ特定の運動量とエネルギーを持った)右辺の状態に遷移すると考えるのが一般的です.
だから力学の式は,
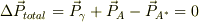
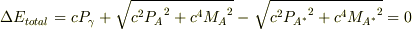 といった感じで全体について考える事しかできません.
またこの式は,反応の起こりやすさ等を考える事(量子力学の範疇)とは完全に独立した計算になっています.
といった感じで全体について考える事しかできません.
またこの式は,反応の起こりやすさ等を考える事(量子力学の範疇)とは完全に独立した計算になっています.
Re: 質点系の力学
mNeji さんのレス (2009/11/29(Sun) 20:55)
ytさん,
せっかくのご説明ですが,私には仰る事が理解出来ません.
勿論,ある問題を多角的に考察する事は大切だと思います.ただ,この問題に付いて論議するに当って,量子力学も相対論も引用するのは必要なのでしょうか.
この問題は,古典力学の範疇で十分に論議できると思います.ただ最初から天下り的に運動方程式を与えても理解しにく考えたので,私の場合は,
・時間を離散的に考えて, ・ロケットと噴出ガスとの2体問題として,立式.
して見たものです.
其れ以外の考え方を提唱されるのは興味深いです.それは,それで,あくまで古典力学の範囲で論ずるべきではないでしょうかね.
Re: 質点系の力学
yt さんのレス (2009/12/01(Tue) 01:05)
mNeji さん 後半のγ崩壊云々は本題からそれた余計な記述だったと思います.反省します. そして mNejiさんの説明方法の方が,「全然わからない」と言っていた質問者にふさわしかったと思います.
ただ...,正直に言ってしまいます. 今回の mNejiさんとのやりとりの中で,悪意は無いと思いますが少し微妙な印象を受ける表現が幾つか見受けられた事を指摘しておきます. 私は最初(No.25974) mNejiさんの計算間違いを指摘しただけなのに,やや皮肉交じりな返し(No.25976)を受けたように感じました. 「私は〜とは知りませんでした」の部分は,文脈上『何を言ってるんですか,そんなわけが無いでしょう(笑)』と小馬鹿にした感じにとれます.被害妄想だと言われるかもしれませんが... 勘違いなら申し訳ありませんが,その後(No.25980)も「噴射ガスの相対速度よりもロケットが速く飛べる」事の確認もしないまま,一方的に話を終了されたように感じました. 「論議はここまでとさせて戴きます」との表現は誤解を招き易いように思います.「今日の処は」といった追加表現が省略されているだけなのか,以降は話を受け付けませんといった感じなのか等々 が判りにくい印象があります. つまらない事に敏感で申し訳ありません.常に良いほうに解釈すべきと思うのですが,少し書きたくなってしまったのです.
Re: 質点系の力学
mNeji さんのレス (2009/12/01(Tue) 01:21)
ytさん,
>ただ...,正直に言ってしまいます. >今回の mNejiさんとのやりとりの中で,悪意は無いと思いますが少し嫌な印象を受ける表現が幾つか見受けらけられた事を指摘しておきます.
そうですね.ご指摘の通りです.やや意識して硬く書きました.というのも,先にかかれた
>後半のγ崩壊云々は本題からそれた余計な記述だったと思います.
の部分などで,質問者の方が萎縮してはいけないかと思ったからです.でも,それを細かく書くと話がこじれてしまうと考えたからです.不愉快な印象をもたれたとするならご免なさい.
>私は最初(No.25974) mNejiさんの計算間違いを指摘しただけなのに,やや皮肉交じりで高圧的な返し(No.25976)を受けたように感じました. 勘違いなら申し訳ありませんが,その後の反応(No.25980)も「噴射ガスの相対速度よりもロケットが速く飛べる」事の確認もしないまま,一方的に終了されたように感じました.
計算間違いは,既に訂正したように私のミスです.「噴射ガス...」の件は,質問者の方が積分をするのを待って論議するつもりでした.
また,敢えて論議していませんでしたが,「g」に関するご論議には幾つか異論があります.これらも出来れば質問者さんの論議に合わせて行きたいと思っております.
取り敢えずの,背景説明とさせて戴きます.
Re: 質点系の力学
yt さんのレス (2009/12/01(Tue) 01:41)
mNeji さん すみません.延々と推敲していたため先の文章は途中で変更してしまいました. 「嫌な」といった表現はあまり使うべきではないと思ったりしたのです.
私のつまらない反応に冷静に付き合ってくださり,ありがとうございます. 今後もたまに書き込みたいと思いますので,よろしくお願いします.
Re: 質点系の力学
mNeji さんのレス (2009/12/01(Tue) 11:16)
ytさん,
>今後もたまに書き込みたいと思いますので,よろしくお願いします.
角度の違う解説はとても大切だと思います.こちらこそ,よろしくお願いします.