projection tensor
projection tensor
aby さんの書込 (2009/11/15(Sun) 15:30)
任意のベクトルを超曲面に射影するprojection tensorは
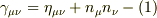 と定義されるそうです.ここで,
と定義されるそうです.ここで, 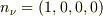 の超曲面に垂直な単位ベクトルです.
任意のベクトル
の超曲面に垂直な単位ベクトルです.
任意のベクトル 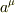 に作用させると
に作用させると
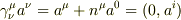 となり,確かにベクトルの空間成分を取り出すのがわかります.
いろいろ調べたところ,このprojection tensorは三次元のmetricになっているそうですが,それを証明することは可能ですか?
上の式を三次元metricの定義として,いきなり導入しているものが多いのですが,僕は「projection tensor=metric tensor」というのが自明とは思えず,気になります.
metricを(1)式のように分解すると,
となり,確かにベクトルの空間成分を取り出すのがわかります.
いろいろ調べたところ,このprojection tensorは三次元のmetricになっているそうですが,それを証明することは可能ですか?
上の式を三次元metricの定義として,いきなり導入しているものが多いのですが,僕は「projection tensor=metric tensor」というのが自明とは思えず,気になります.
metricを(1)式のように分解すると, 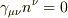 となるから,
となるから, 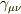 はmetricの空間部分だよ,という論理は成り立ちますでしょうか?
はmetricの空間部分だよ,という論理は成り立ちますでしょうか?