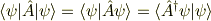ブラケットと演算子

ブラケットと演算子

degi さんの書込 (2009/11/15(Sun) 04:25)

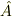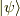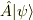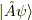演算子 \hat{A} と状態 |\psi \rangle があるとき， \hat{A}|\psi \rangle と |\hat{A} \psi \rangle はどちらも同じなのでしょうか？そもそも，演算子を状態ケットの中に入れるというのはいいのでしょうか？

Re: ブラケットと演算子

yt さんのレス (2009/11/15(Sun) 13:03)

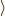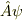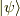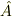記号「｜」と「 \rangle 」の間のシンボルは特定の状態を表すラベルに過ぎません． 「 \hat{A}\psi 」は，状態ケット |\psi \rangle に演算子 \hat{A} を作用させた状態を表すラベルであると見做す暗黙ルールがあるようです． よって以下のような感じで使い分けられるていると思います． 例. 運動量演算子(座標表示)

\hat{p}\,|\psi\rangle =\left[ \frac{\hbar}{i} \left(\begin{array}{ccccc}\ddots & {\small +1/2\delta q} & 0 & 0 & 0 \\{\small -1/2\delta q} & 0 & {\small +1/2\delta q} & 0 & 0 \\0 & {\small -1/2\delta q} & 0 & {\small +1/2\delta q} & 0 \\0 & 0 & {\small -1/2\delta q} & 0 & {\small +1/2\delta q} \\0 & 0 & 0 & {\small -1/2\delta q} & \ddots \end{array}\right) \right]\left(\begin{array}{l}\;\;\vdots \\\psi({\small q -\delta q}) \\\psi({\small q }) \\\psi({\small q +\delta q}) \\\;\;\vdots \end{array}\right)\\= \left(\begin{array}{l}\;\;\vdots \\\frac{\hbar}{i} \partial_{\tiny q}{\psi}({\small q -\delta q}) \\\frac{\hbar}{i} \partial_{\tiny q}{\psi}({\small q }) \\\frac{\hbar}{i} \partial_{\tiny q}{\psi}({\small q +\delta q}) \\\;\;\vdots \end{array}\right)=|\hat{p}\,\psi\rangle

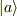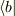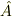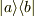結局，同じなので違いを気にする必要はありません． ちなみにケット |a\rangle はヒルベルト空間上の列ベクトル，ブラ \langle b| は行ベクトル， \hat{A} や |a\rangle \langle b| は行列に対応していますが 各成分の値は，基底の採り方(座標表示,運動量表示, etc.)によって異なります． ブラ・ケットを使うと基底の採り方によらない議論ができて便利です． 例えば以下のような感じで・・・

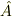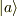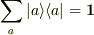一般にエルミート演算子 \hat{A} の固有ベクトル |a\rangle は完全正規直交系をなすように採れます． (無限次元での扱いはややこしいので，この辺は有限次元からの類推で済ませておきます．) この事から， \sum_{a}|a\rangle \langle a| = \bf{1} となる事が示せます． なぜなら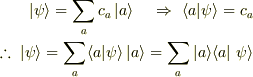， |\psi\rangle = \sum_{a} c_{a}\,|a\rangle \;\;\;\; \Rightarrow \; \langle a|\psi\rangle = c_{a} \\ \;\;\;\; \therefore \; |\psi\rangle = \sum_{a} \langle a|\psi\rangle\,|a\rangle = \sum_{a}|a\rangle \langle a|\;\psi\rangle これが任意の 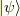|\psi \rangle に対して成り立つので．

Re: ブラケットと演算子

degi さんのレス (2009/11/27(Fri) 21:19)

なるほど．どちらでもいいわけですか．

\langle \psi | \hat{A} | \psi \rangle=\langle \psi | \hat{A} \psi \rangle=\langle \hat{A}^\dagger \psi | \psi \rangle

みたいな変形も構わないわけですね？

Re: ブラケットと演算子

yt さんのレス (2009/11/28(Sat) 09:59)

ですね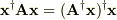． \mathbf{x}^\dagger \mathbf{A} \mathbf{x} = (\mathbf{A}^\dagger \mathbf{x})^\dagger \mathbf{x} 結局，(複素数)行列と同じです．だからブラケット記法特有のルールで覚えるべき事はあまりないと思います．

Re: ブラケットと演算子

degi さんのレス (2009/11/29(Sun) 20:16)

ブラケットは使えるようになると便利なんでしょうね．

どうもありがとうございました！