逆格子について

degi さんの書込 (2009/11/11(Wed) 02:46)

まず，逆格子とは何なのでしょうか？初学者にわかりやすく説明してもらえないでしょうか？できれば，まず「逆格子とは…」と書いて，それから利点などを説明していただけるとありがたいです．光や電子は波の性質を持つから，それを議論するためには運動量空間がいいということなのでしょうか？

つぎに逆格子ベクトルの話が出ると思うのですが，その定義には平面波exp(ik・r)を考えますよね．どうして平面波が出てくるのでしょうか？X線回折なんかと関係しているのでしょうか？

逆格子の基本並進ベクトルはb1=2π(a2×a3)/(a1・a2×a3)などと書かれます．逆格子ベクトルはexp(ik・r)=1を満たすものと定義されると思いますが，ここからどうやってb1などが導かれるのでしょうか？こういう風に定義すればうまくいくから？それとも別の要請があるのでしょうか？

Re: 逆格子について

mNeji さんのレス (2009/11/12(Thu) 13:53)

degiさん，

私も，この手の論議が得意でないのですが，説明を試みてみます．

まず，「運動量空間...」と考えるより，対象が「周期性をもった結晶」なので，フーリエ級数展開をすると考える方が自然ではないでしょうか．ただ，結晶は常に「食塩」のように直方体のように直交した格子だけでなく，「方解石」のように直方体が押し潰された様な斜交した格子をも相手にしなければならないので，表現が複雑になっているのだと思います．

で，逆格子を説明するのは難しいので，たとえば，「305 逆格子空間」のサイト http://www.f-denshi.com/000okite/300crstl/305cry.html の解説をご覧になって判らない所があれば，その箇所についてご質問されたらと思います．

なお，「逆格子の基本並進ベクトルはb1=2π(a2×a3)/(a1・a2×a3)」ですが，基本は，「b1 ∝a2×a3」で，その他は規格化の為の係数と考えたらいかがでしょうか？大切なのは，「b1」は「a2」「a3」とに直交することが保証されている事だと思います．

Re: 逆格子について

degi さんのレス (2009/11/13(Fri) 02:44)

>まず，「運動量空間...」と考えるより，対象が「周期性をもった結晶」なので，>フーリエ級数展開をすると考える方が自然ではないでしょうか．

逆格子の定義で平面波が出てくるのは，結晶の周期性をうまくあらわせるから？でしょうか？

あるページで光などは 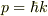$p=\hbar k$ の運動量を持つからk空間がいいんだというような話を書いてあったので光や電子たちにとっては波数空間のほうが重要なのかな？と考えたりもします．

305 逆格子空間のサイトを見させてもらいました．

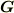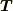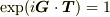逆格子ベクト $\bm{G}$ の定義は並進操作 $\bm{T}$ に対して $\exp(i\bm{G}\cdot \bm{T})=1$ を満たすことですが，この式から 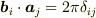$\bm{b}_i \cdot \bm{a}_j=2\pi \delta_{ij}$ が分かるのでしょうか？それともこれはこのようにおくと便利だということでしょうか？

あと，少し話がそれますが，X線回折の「回折」というのはどういうことですか？X線回折ではX線は電子のポテンシャルを感じて散乱されるのですよね？回折というのは波が物体の後ろとかに回り込むことだと思っているのですが，散乱時に回折が起きているということでしょうか？X線反射と言ったほうが直観的な気がします．

Re: 逆格子について

mNeji さんのレス (2009/11/13(Fri) 11:11)

＞逆格子の定義で平面波が出てくるのは，結晶の周期性をうまくあらわせるから？

やはり，初めの段階では「平面波」と解釈するよりも，元素とか電子の配置に「結晶の周期性」を反映すると，フーリエ級数展開を適用するのが自然だからだと思います．

そのような結晶系に「平面波」が入射してきて，結晶から散乱を生じるときに，はじめて平面波との関係が明確になるのではないでしょうか．

＃ただし，私は，数学が余り得意ではないので，厳密な説明はできませんので，悪しからず．＃もし「厳密な説明」がお望みでしたら，他の方に助言をお求めになってください．

＞あるページで光などは 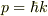$p=\hbar k$ の運動量を持つからk空間がいいんだというような話を書いてあったので光や電子たちにとっては波数空間のほうが重要なのかな？と考えたりもします．

色々な解釈がありそうですが，周期性に着目する限り，「波数」で考えるのが自然だと思います．

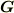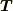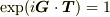＞逆格子ベクト $\bm{G}$ の定義は並進操作 $\bm{T}$ に対して $\exp(i\bm{G}\cdot \bm{T})=1$ を満たすことですが，この式から 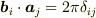$\bm{b}_i \cdot \bm{a}_j=2\pi \delta_{ij}$ が分かるのでしょうか？それともこれはこのようにおくと便利だということでしょうか？

この所をどう理解するかが重要だと思います．私が学生の頃に読んだテキストでは，この説明が天下り的で納得が行かなかったきがします．

例えば物理量として，一次元の電子の存在確率を 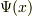$\Psi(x)$ が，格子を持った，周期関数である場合，

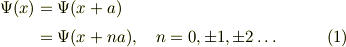
$\Psi(x)&=\Psi(x+a)\\&= \Psi(x+na), \quad n = 0, \pm 1, \pm 2 \dots &\ (1)$

を満たします．直感的には複素形式の三角関数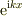， $\mathrm{e}^{\mathrm{i}kx}$ を考えると，式(1)の周期条件から 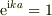$\mathrm{e}^{\mathrm{i}ka}=1$ を満たすが，指数関数は周期 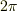$2\pi$ を持つから，

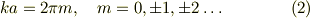
$ka &= 2\pi m, \quad m = 0, \pm 1, \pm 2 \dots &\ (2)$

従って，波数は，逆格子の整数倍に制限される；

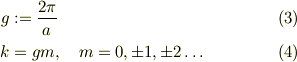
$g &:= \frac{2\pi}{a} &\ (3)\\k &= gm, \quad m = 0, \pm 1, \pm 2 \dots &\ (4)$

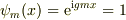特定のについての $\psi_m(x) = \mathrm{e}^{\mathrm{i}gmx}=1$ は，この系の直交関数系を成します;

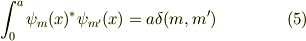
$\int_0^a\psi_m(x)^* \psi_{m'}(x) &= a\delta(m,m') &\ (5)$

同様に，３次元の直交格子では，3つの格子ヴェクタ，

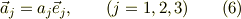
$\vec a_j = a_j \vec e_j, \qquad (j=1,2,3) &\qquad (6)$

に対して，3つの逆格子ヴェクタ

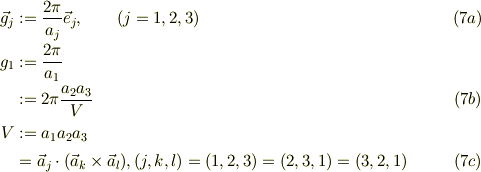
$\vec g_j &:= \frac{2\pi}{a_j} \vec e_j, \qquad (j=1,2,3) &\qquad (7a)\\g_1 &:= \frac{2\pi}{a_1} \\&:= 2\pi \frac{a_2 a_3 }{V} &\qquad (7b)\\V &:=a_1 a_2 a_3\\&= \vec a_j \cdot ( \vec a_k \times \vec a_l), (j,k,l) =(1,2,3)=(2,3,1)=(3,2,1) &\qquad (7c)$

について，波数ヴェクタ 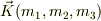$\vec K(m_1, m_2, m_3)$ として，

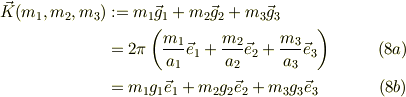
$\vec K(m_1, m_2, m_3) &:= m_1\vec g_1 +m_2\vec g_2 +m_3\vec g_3 \\&= 2\pi\left( \frac{m_1}{a_1}\vec e_1+\frac{m_2}{a_2}\vec e_2 +\frac{m_3}{a_3}\vec e_3\right) &\qquad (8a)\\ &= m_1 g_1\vec e_1 +m_2 g_2\vec e_2 +m_3 g_3\vec e_3 &\qquad (8b)$

とすると，

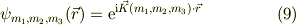
$\psi_{m_1, m_2, m_3}(\vec r) &= \mathrm{e}^{\mathrm{i}\vec K(m_1, m_2, m_3) \cdot \vec r }&\ (9)$

は，この系の直交関数系となります．

同様に，斜交格子について，(6)~(9)を拡張したのが今回のご質問に対応するのではないでしょうか？

＞X線回折の「回折」というのはどういうことですか？

上手く言えないのですが，十分遠方にある線源(電磁波，中性子，電子，etc)からでは波は，結晶に来るまで，球面波で到達します．そこでそれぞれの結晶の原子団に侵入し，そこから球面波として放出(散乱)されて行きます．この球面波はそれぞれのサイトからの重ね合わせですから，ある方向に依存した干渉パターンを生成します．実際のパターンの論議には，線源の種類，結晶のモデル化などの具体的な事が判らないといけませんね．

其の意味では「散乱」とか「回折」とか言えても，「反射」とは現象がことなるような気もします．ただ，あまり自信はありません．

Re: 逆格子について

ぶどうさんのレス (2009/11/16(Mon) 01:04)

逆格子の利点は分かりませんが，単にLEEDで観察される結晶格子が逆格子像だから使われていると思っていました．

Re: 逆格子について

degi さんのレス (2009/11/27(Fri) 21:12)

返事が遅れて申し訳ありません．

>同様に，斜交格子について，(6)~(9)を拡張したのが今回のご質問に対応するのではないでしょうか？

斜交格子ではa1,a2,a3は直交しないので，ちょっと難しくなりますよね？ちょっと考えてみたいと思います．

LEEDというのは初めて知りました．逆格子像が見えるんですか．ちょっと検索してみましたが，きれいな像が見えるみたいですね．

みなさんどうもありがとうございました．

[home] [掲示板] [ページの先頭]