正準変換について

正準変換について

るんるん さんの書込 (2009/11/05(Thu) 00:25)

はじめまして，るんるん（大学３年）といいます．

「量子力学を学ぶための解析力学入門」の演習問題４(7)で， q,pをそれぞれ一般化座標，一般化運動量としたとき， q[i]→Q[i]=Σ[j=1,n]a[i,j]q[j] （a[i,j]は正則行列Aの(i,j)成分） P[i]→p[i]=Σ[j=1,n]a[i,j]P[j] という変換(q,p)→(Q,P)は正準変換である．と，書かれているのですが， Q=Aq,P=A^(-1)pで (A^(-1)はAの逆行列）(q,p)から(Q,P)への写像Fを定義すると Aが対称行列でなければ，(∂F/∂z)'J(∂F/∂z)≠J(z=(q,p)）となり，この 変換は必ずしもシンプレクティック変換とはなりません． 正準変換≠シンプレクティック変換なのでしょうか？ 基本的な質問かと思いますが，よろしくお願いします．

Re: 正準変換について

HGUCクシャトリアかっこいい さんのレス (2009/11/12(Thu) 22:31)

私も同じ本(第８刷)を持っていたので確認したのですが，ここは誤植ですね． 少し記法は変わりますが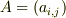， A=(a_{i,j}) として母関数を 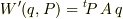W'(q,P) = {}^t\!P \,A \,q のように取ると以下のようになりました．

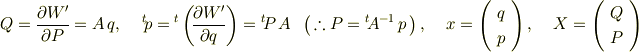
Q = \frac{\partial{W'}}{\partial{P}} = A\,q ,\mspace{20mu}{}^t\!p = {}^t\left(\!\frac{\partial{W'}}{\partial{q}}\right) = {}^t\!P\,A \mspace{10mu} \left(\,\therefore P = {}^t\!A^{-1}\,p \,\right) ,\mspace{20mu}x = \left(\begin{array}{c}q \\p \\\end{array}\right),\mspace{20mu}X = \left(\begin{array}{c}Q \\P \\\end{array}\right)
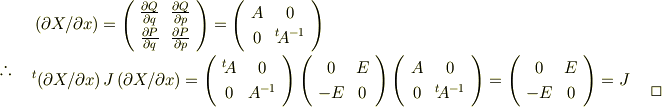
& \left(\partial{X}/\partial{x}\right)=\left(\begin{array}{cc}\frac{\partial{Q}}{\partial{q}} & \frac{\partial{Q}}{\partial{p}} \\\frac{\partial{P}}{\partial{q}} & \frac{\partial{P}}{\partial{p}} \\\end{array}\right)=\left(\begin{array}{cc}A & 0 \\0 & {}^t\!A^{-1} \\\end{array}\right)\\{{\therefore}\atop{}} \mspace{20mu}& {}^t\!\left(\partial{X}/\partial{x}\right)J\left(\partial{X}/\partial{x}\right)=\left(\begin{array}{cc}{}^t\!A & 0 \\0 & A^{-1} \\\end{array}\right)\left(\begin{array}{cc}0 & E \\-E & 0 \\\end{array}\right)\left(\begin{array}{cc}A & 0 \\0 & {}^t\!A^{-1} \\\end{array}\right)=\left(\begin{array}{cc}0 & E \\-E & 0 \\\end{array}\right)=J \mspace{20mu} {{}\atop{\Box}}

数式掲示版は初めて利用しますが綺麗に表示されて楽しいですね．