フーリエ変換

ヒロさんの書込 (2009/10/29(Thu) 01:44)

大学２年生で物理を学んでいます．フーリエ変換の問題なのですが，以下の問題が出来ません．ただ単に積分の問題として解く実力がないのか，別の手法があるのかどうかも分かっていないので，どなたか分かる方よろしくお願いします．

↓↓以下問題文↓↓

以下の関数を 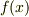f(x) のフーリエ変換という．

$\int_{-\infty}^{\infty}\frac{dx}{\sqrt[]{\mathstrut 2\pi}}f(x)e^{-ikx}$

$\int_{-\infty}^{\infty}\frac{dx}{\sqrt[]{\mathstrut 2\pi}}\frac{1}{1+(\frac{x}{a})^2}e^{-ikx}$

$\int_{-\infty}^{\infty}\frac{dx}{\sqrt[]{\mathstrut 2\pi}}e^{-\frac{1}{2}(\frac{x}{a})^2}e^{-ikx}$

を解け．

これも複素積分の問題です．適当なテキストに記載されているはずです．

ヒロさん，

(1)に付いては，こちらのサイトのクロメルさんの資料；

が，結構参考になると思います．

(2）については，指数部を纏めて，それを平方完成に持ち込むのはどうですか？