波動関数について

波動関数について

零 さんの書込 (2009/10/24(Sat) 00:25)

はじめまして，零といいます．

波動関数の規格化についての質問なのですが，ψ(x)=C2'sin(nπ/ax) (n=1,2,3..) の式において規格化の条件を満たすC2'を求めよ，という問題の解き方が全く分かりません．

授業では，∫(-∞→∞)|ψ(x)|^2dx=∫(0→a){ψ(x)}^2dx＝1

と説明されたのですが，真ん中の式のように0→aの条件で解いてC2'を求めればいいのでしょうか？

Re: 波動関数について

mNeji さんのレス (2009/10/25(Sun) 08:16)

零さん，初めまして．

問題とされている系がどのような条件なのかが明確にならないと説明し難いと感じますが...．

少なくとも，波動関数の定義領域が，(-∞→∞)なのか，(0→a)かで，問題が別になってしまいますよね．

Re: 波動関数について

ASA さんのレス (2009/10/25(Sun) 12:09)

定義領域は(-∞→∞)の単なる計算問題です． 留数応用の複素積分として有名な∫{sin^2(y)/y^2}dy=πの計算に帰着できます．

Re: 波動関数について

零 さんのレス (2009/10/25(Sun) 22:21)

mNejiさん あまり物理に詳しくないので系かどうかはわからないのですが，1次元自由粒子の波動関数です

定義領域は問題では(-∞→∞)とされています

ASAさん ということは，答えは Ｃ2'=±ax/nπ√1/π でしょうか？

Re: 波動関数について

mNeji さんのレス (2009/10/25(Sun) 22:34)

＞1次元自由粒子の波動関数です と ＞定義領域は問題では(-∞→∞)とされています とすると，

＞授業では，∫(-∞→∞)|ψ(x)|^2dx=∫(0→a){ψ(x)}^2dx＝1 に違和感を受けます．

なお， ＞ψ(x)=C2'sin(nπ/ax) (n=1,2,3..) これは，

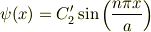
\psi(x) =C_2'\sin\left(\frac{n\pi x}{a}\right)

の事ですか？

Re: 波動関数について

零 さんのレス (2009/10/25(Sun) 22:46)

いえ，sinのカッコの中身が微妙に違います

xが分子ではなく分母にあります

Re: 波動関数について

mNeji さんのレス (2009/10/25(Sun) 22:58)

＞xが分子ではなく分母にあります

やはりそうですか．すると「x，a」は無次元の量ですかね．

Re: 波動関数について

零 さんのレス (2009/10/25(Sun) 23:10)

すいません，そこまでは配られた資料には書いてないです

Re: 波動関数について

mNeji さんのレス (2009/10/26(Mon) 00:11)

私には回答出来ません，悪しからず．

Re: 波動関数について

零 さんのレス (2009/10/26(Mon) 07:28)

そうですか... mNejiさん，ありがとうございました

Re: 波動関数について

零 さんのレス (2009/10/26(Mon) 10:26)

mNejiさん

先程，先生に聞いた所，もらった資料が間違えていたらしいです

正しくはmNejiさんの提示した式の通り，xは分子にあります

Re: 波動関数について

mNeji さんのレス (2009/10/26(Mon) 11:53)

＞xは分子にあります

という事なら，外力が無い場合の両端が束縛された定常波動のように思えます．係数を求める為には正弦波の自乗の積分ですから，倍角の公式を使えば求まりませんか？

他方，波動関数の定義領域については，「No.23841，一次元箱形ポテンシャル，えりさん」のスレッドを見ると感じが掴めるかも知れません．

Re: 波動関数について

零 さんのレス (2009/10/26(Mon) 12:41)

出来ました！ Ｃ2'=√2／√aですよね？

ただ，符合はどうなるのでしょうか？ ±のままつけていいのですか？

Re: 波動関数について

mNeji さんのレス (2009/10/26(Mon) 15:41)

＞Ｃ2'=√2／√aですよね？

n依存性が落ちていませんか？

波動関数は任意位相， \mathrm{e}^{\mathrm{i}\phi} の任意性がありますね．境界条件を付ける前は，適当な係数を付けておき，その後は係数を固定すればいいのだと思います．

Re: 波動関数について

mNeji さんのレス (2009/10/26(Mon) 18:40)

この手の計算では，オイラーの公式を使うと計算が簡単になることが解り易いのでご紹介します．私は，三角関数をよく間違えるので，オイラー公式；

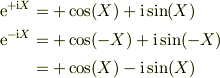
\mathrm{e}^{+\mathrm{i}X} &= +\cos(X) +\mathrm{i}\sin(X)\\\mathrm{e}^{-\mathrm{i}X} &= +\cos(-X) +\mathrm{i}\sin(-X)\\&= +\cos(X) -\mathrm{i}\sin(X)

と，この逆；

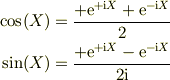
\cos(X) &= \frac{+\mathrm{e}^{+\mathrm{i}X}+\mathrm{e}^{-\mathrm{i}X}}{2}\\\sin(X) &= \frac{+\mathrm{e}^{+\mathrm{i}X}-\mathrm{e}^{-\mathrm{i}X}}{2\mathrm{i}}

とをよく使っています．指数関数なら，積とか微積分が機械的に処理できるので，三角関数より計算に紛れ難いのが自慢です．

そこで積分する関数をオイラーの公式で表現する為に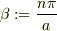， \beta := \frac{n\pi}{a} として；

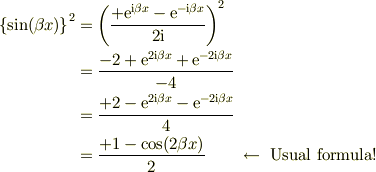
\left\{\sin(\beta x)\right\}^2&= \left( \frac{+\mathrm{e}^{\mathrm{i}\beta x}-\mathrm{e}^{-\mathrm{i}\beta x}}{2\mathrm{i}} \right)^2\\&= \frac{-2+\mathrm{e}^{2\mathrm{i}\beta x}+\mathrm{e}^{-2\mathrm{i}\beta x} }{-4}\\&= \frac{+2-\mathrm{e}^{2\mathrm{i}\beta x}-\mathrm{e}^{-2\mathrm{i}\beta x} }{4}\\&= \frac{+1-\cos(2\beta x)}{2} \qquad \leftarrow\ \text{Usual formula!}

従って，辺々をxについて 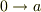0 \to a の範囲で積分すると；

\int_0^a \left\{\sin(\beta x)\right\}^2 \mathrm{d}x&= \int_0^a \frac{+2-\mathrm{e}^{2\mathrm{i}\beta x}-\mathrm{e}^{-2\mathrm{i}\beta x} }{4} \mathrm{d}x\\&= \frac{1}{4}\left[ +2x-\frac{\mathrm{e}^{2\mathrm{i}\beta x}}{\beta}-\frac{-\mathrm{e}^{-2\mathrm{i}\beta x}}{-\beta} \right]_0^a\\&= \frac{1}{4}\left[ +2(a-0)-\frac{\mathrm{e}^{2\mathrm{i}\beta a}-1}{\beta}-\frac{-\mathrm{e}^{-2\mathrm{i}\beta a}-(-1)}{-\beta} \right]

ここで，右辺の２つの分数の分子部分は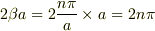， 2\beta a =2\frac{n\pi}{a} \times a = 2n\pi の為に，消滅するから，

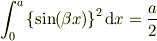
\int_0^a \left\{\sin(\beta x)\right\}^2 \mathrm{d}x&= \frac{a}{2}

となる．

おっと，n依存性は無い様ですね(汗)．ご免なさい(笑)．

Re: 波動関数について

零 さんのレス (2009/10/26(Mon) 23:43)

mNejiさん，最後まで教えて下さり，また簡単なやり方まで教えて下さってとても助かりました．

本当にありがとうございました