回転運動での向心力や遠心力の解釈
回転運動での向心力や遠心力の解釈
mNeji さんの書込 (2009/10/20(Tue) 15:10)
■現在工事中■ 〜〜〜〜〜 ●このスレッドを書くにあたって●
緋色さんが立てられたスレッド,【遠心力】,2009/10/12(Mon) 17:43 No.25673 が発端で高校物理IIをいくつか拝見する機会がありました.そこで,今拝見しても,高校の教科書が理解出来なくて愕然としました.
というのも,私は,大昔にも高校物理の教科書が理解出来なくて,教科書から落ちこぼれた苦い経験が在ります.其の為に,自力更生という,イバラの道を歩んだと思っています(笑).
でも,大学生の目線でなら回転運動や,向心力,遠心力を説明出来るかも知れないと思うようになりました.そこで,自分が,大学新2年生ぐらいだとして,説明してみようかと思います.残念なことに私は数学も苦手なので,可笑しい点がありまあしたら,ご助言をお願いします.また意味不明の点などありましたら,ご指摘ください.
〜〜〜〜〜 ● 解くべき問題●
誰もが小学生のころ遊んだように,「消しゴム」のような錘に,「たこ糸」を結び,指で糸の端を掴んで,くるくると回したような状態を解きたいと思います.そこで,問題を次の様に定めます;
摩擦が無視できるような理想的平面上の一点Oに「ピン」が立っていて,そこに「質量」や「伸び」無視出来る理想的な「糸」(長さR)を結び,他の端点を質量mの錘Wに結ぶとする.この錘は水平面上を摩擦なしで運動出来るとする.また糸とピンの接触部は十分に細く,摩擦も無いとする.
図1のように,点Oを原点とした静止座表系Oxyを考え,錘Wの初期条件として,位置は(R,0),速度は(0,V),であったとする.
摩擦は一切無いので,錘に働く力は,求心力(糸の張力)だけで,その大きさTは一定とする. <pre> 図1静止座標系
y軸 ↑ | |
y・ーーーーーーー・W
|/| |/| |/| |/| |/| |/| |/| ーーーーーーーーーーーーー+ーーーーーーー・ーーーーー→x軸 O|x |
</pre>
このとき,
(1)静止座標系での座標値(x,y)として,運動方程式を求め,その解を論ぜよ.
(2)回転座標系として,Oxyのx軸から反時計方向に角度 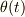 ,原点からの動径方向の長さを
,原点からの動径方向の長さを 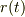 として,運動方程式を求め,その解を論ぜよ.
として,運動方程式を求め,その解を論ぜよ.
とします.
● 回答1:静止座標系 ●
原点Oにたいする質点Wの位置ヴェクタと糸の長さに関して;
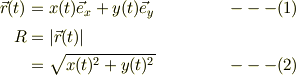
質点Wに摩擦は皆無なので,働く力 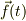 としては,張力(向心力)だけなので,
としては,張力(向心力)だけなので,
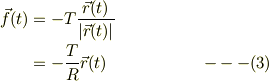
運動方程式は
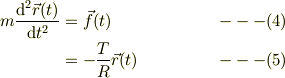
であるから,それぞれの成分毎に同一の単振動挙動の微分方程式になっている;
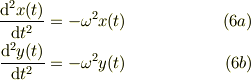
ここで,便宜的に変数を定義した;

従って,式(6)の解は正弦波,余弦波の線形和であり,その係数(a,b,c,d)は初期条件で決まる;
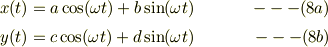
速度はこれらの時間微分だから,
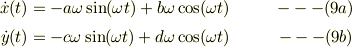
これらに初期条件を適用すると
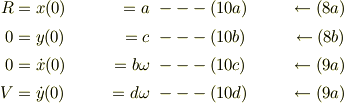
従って,
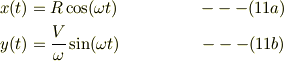
となる.この係数には,式(2)の束縛条件が時間に寄らずに成立する事から,

の関係がある.図形的には,  が回転角速度である事を意味する.従って,式(7)から,張力を
が回転角速度である事を意味する.従って,式(7)から,張力を

と表現出来る.
ところで,式(12)で式(11)を書き換えれば,単に

となって, 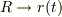 ,
, 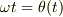 とすれば,通常の位置ヴェクタの極座標表示になっているのは,注目すべきです.ということで次に進みましょう.
とすれば,通常の位置ヴェクタの極座標表示になっているのは,注目すべきです.ということで次に進みましょう.
● 回答2:回転座標系 ●
まずは図から,
<pre> 図2回転座標系
y軸
↑ 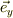 |
|  |
| 
y・・W
|/
|/
|/|OW|= r(t)
|/
|/
|/∠WOx = θ(t)
|/ 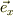 ーーーーーーーーーーーーー+ーーーーーーー・ーーーーー→x軸
O|x
|
ーーーーーーーーーーーーー+ーーーーーーー・ーーーーー→x軸
O|x
|
</pre>
位置ヴェクタを原点からの動径距離 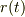 と,x軸からの回転角
と,x軸からの回転角 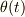 で表すと;
で表すと;
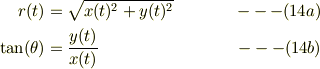
式(1)について書き換えると;
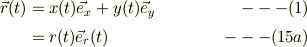
ここで, 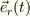 は動径方向の単位ヴェクタで質点の動きにあわせて変化するという意味では,加速度系の基底単位ヴェクタであることに注意したい.
は動径方向の単位ヴェクタで質点の動きにあわせて変化するという意味では,加速度系の基底単位ヴェクタであることに注意したい.
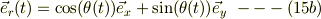
従って,速度ヴェクタ 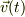 を考える時,位置ヴェクタの動径半径
を考える時,位置ヴェクタの動径半径 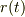 だけでなく基底ヴェクタ
だけでなく基底ヴェクタ 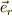 についても微分を考える必要があるのが面倒ですが,後で考え易くなる為に頑張ってみましょう.
についても微分を考える必要があるのが面倒ですが,後で考え易くなる為に頑張ってみましょう.
![\vec v(t)&= \frac{\mathrm{d}\vec r(t)}{\mathrm{d} t}\\&= \frac{\mathrm{d}r(t)\vec e_r(t)}{\mathrm{d} t}\\&= \dot r(t)\vec e_r(t) + r(t)\frac{\mathrm{d}\vec e_r(t)}{\mathrm{d} t}\\&= \dot r(t)\vec e_r(t) + r(t)\frac{\mathrm{d}\vec e_r}{\mathrm{d} \theta}\frac{\mathrm{d}\theta(t)}{\mathrm{d} t}\\&= \dot r(t)\vec e_r(t) + r(t)[-\sin(\theta)\vec e_x +\cos(\theta)\vec e_y]\dot \theta(t)\\&= \dot r(t)\vec e_r(t) + r(t)\dot \theta(t)\vec e_{\theta}(t) &\ ---(16a)](http://hooktail.maxwell.jp/bbslog/1d225398132e12c391b81ce86a558f6c.png)
ここで接線方向の基底ヴェクタを導入した;
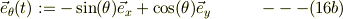
同様に加速度ヴェクタ 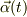 を求めると;
を求めると;
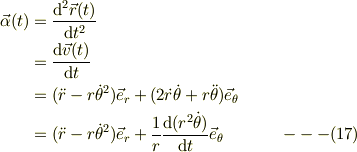
やっと準備が終わったので,向心力の式(3),運動方程式(5)に極座標表現を用いれば,向心力は
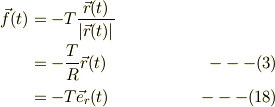
運動方程式は

に注意して,加速度座標系の基底ヴェクタの成分について,二つの運動方程式に分解する事が出来ます;
動径方向について

接線方向について

となります.
動径方向の運動方程式(19a)を整理して書き直すと,
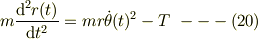
となります.これこそが,中心力が働く場合,その動径方向の中心点からの距離が一定となる場合,すなわち,上式の左辺がゼロとなる場合には,遠心項 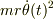 が向心力
が向心力 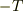 とバランスすることを示しています.
とバランスすることを示しています.
もし向心力が重力のように動径方向の関数ならば,動径方向の運動方程式は微分方程式として解かなくてはなりません.重力の系が,楕円,放物線,双曲線などの解をもつのはこの為です.
他方,接線方向の運動方程式は,向心力だけの系では,角運動量が保存されることを意味しますが,今回は説明を省略します.
● 似て非なるもの ●
同じような回転系でも,地球の回転とともに動く地表の座標系での運動は,今回の回転系と「似て非なるもの」事である点を注意すべきだと思います.
基底ヴェクタが回転するという意味では,数学的表現が同じですが,地表の座標系の問題では,その座標系の中での運動を考える訳です.従って見掛の力,ないしは加速度項は遠心項(力)だけでなく,コリオリ項(力)なども出て来る訳ですね.
それを承知の上で,「似て非だけど,考え方は同じ」として理解すれば,回転現象をイメージし易くできるのだと思います.
● 2次元ヴェクタと複素数表記●
今回の説明は,通常の2次元ヴェクタを用いましたが,それをオイラーの式をつかった複素数表記に慣れておくと,手計算を急にするときに役立ちます.
■検討中■