相対論的体積素片
相対論的体積素片
aby さんの書込 (2009/10/18(Sun) 16:57)
www.a.phys.nagoya-u.ac.jp/~taka/lectures/cosmology/webfiles/cosmology-web/node113.html
上のサイトで勉強しているのですが，
「ローレンツ不変な体積素片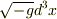 
」
という記述があり，そこが納得できずにいます．
簡単のため，計量はミンコフスキーだとします．
静止系Sから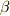 
でx方向に運動する系S'に座標変換した際， 
, 
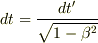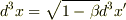とローレンツ変換されるので，四次元の体積 
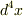は余計なファクターがキャンセルされてローレンツ不変になりますが，時間成分と空間成分を勝手に分離してしまうと，ローレンツ不変量にならないのではないのでしょうか？
Re: 相対論的体積素片
Yokkun さんのレス (2009/10/18(Sun) 21:23)
そのとおりだと思います．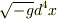 
は，ローレンツ不変（共変的）な時空体積素片ですが， 
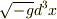が単独で不変にはならないのではないでしょうか？4次元体積素片のことをいおうとして先走った表現なのではないのかと疑っています．
Re: 相対論的体積素片
aby さんのレス (2009/10/19(Mon) 00:31)
＞4次元体積素片のことをいおうとして先走った表現なのではないのかと疑っています． すぐ次の行で，ローレンツ不変な作用の話があるので，ただの日本語のミスかもしれませんね． ありがとうございました．
