MEGAMAN さんの書込 (2009/10/17(Sat) 18:46)

また質問があります． 今度はコンデンサーについてです．

問題は下のURLです． ttp://www.picamatic.com/view/5574527_%E3%82%B3%E3%83%B3%E3%83%87%E3%83%B3%E3%82%B5%E3%83%BC/

この問題の問6について質問なのですが，この操作を無限回繰り返すと，S,a,bが等電位になるらしいのですが，どうして等電位になるのかが分かりません・・・・

あと，この問題を漸化式をもちいて解こうとおもい自分でやってみたのですが，上手くいきませんでした・・・・

どなたか漸化式を用いて問6を解いていただけないでしょうか・・・・

ちなみに答えは，

問4 2CV/3 問5 14CV/27 問6 CV/2

です．

よろしくお願いします．

Yokkun さんのレス (2009/10/17(Sat) 21:26)

>どなたか漸化式を用いて問6を解いていただけないでしょうか・・・・

これは，計算練習としては勉強になりますが，実戦ではとてもおすすめできるものではありません．その計算をやるくらいなら，問い６は捨てた方がましだと思います．半定量的にどうなっていくかを理解する方が，物理を理解したことになるのではないでしょうか？底辺を容量，高さを電圧として面積が電気量になるような長方形を３つならべて，その変化を追跡するのも一考です．底面を容量，水位を電圧，水量を電気量とする筒形の容器を３つ考えるわけです．

1a) まず，C1，C2が等量に充電されます． 1b) C2の電気量の1/3がC3に分けられます．すると，C2の電気量・電圧はもとの2/3に減ります． 2a) 合計電圧が下がったのを埋めるべく，C2の正極板からC1の負極板に電荷が移動して，全体がVに復活します．C2の電気量・電圧はさらに下がります． 2b) C3の方が電圧が高いので，C3からC2に電荷が移動します．C2の電気量・電圧は増加します． 3a) 合計電圧が上がったのを解消すべく，C1の負極板からC2の正極板に電荷が移動します．C2の電気量・電圧はさらにあがります． 3b) ・・・

さて，C2の電気量・電圧はこうして上下をくりかえします．しかし，その移動幅はしだいに小さくなっていくことを確認するのに，そう手間はかからないでしょう．そしてその上下は， a) Sとaの電位を同じくする b) Sとbの電位を同じくする という操作の下に起こっているのですから，最終的にS,a,bの電位は１点に収束するわけです．

ちなみに，水のモデルでいえば，いずれも水量（電気量）を変えないという条件の下で a) C1とC2の水位（電圧）の和をVにする b) C2とC3の水位（電圧）をそろえる という操作になります．C2はC1とC3の間で水（電荷）を動かしているだけです．

ポイントは，全コンデンサの電気量の合計は常に保存されているという点です．

結果的に，電気量保存からC2の最終電荷は，S,a,bをつないだ回路の場合のものに同じくなるということですね．

MEGAMAN さんのレス (2009/10/17(Sat) 22:27)

Yokkunさん，詳しい説明を本当にありがとうございます． とても分かりやすかったです．

Yokkunさんの仰せられる通り，やはり物理の問題は物理現象を頭の中で考察していきながら解いていくのがもっとも理解を深める近道ですよね．

とても勉強になりました．

Yokkun さんのレス (2009/10/17(Sat) 23:59)

大分，間違いがありましたので，おわびとともに訂正です． C1とC2の電荷のやりとりでは，両コンデンサの電気量の合計は保存されません． ただし，C1の負極板とC2の正極板の電気量の和は保存されるということですね． したがって， 「全コンデンサの電気量の合計は常に保存されている」 というのは間違いで，-Q1+Q2+Q3=0 が保たれているというのが正しい． C2の電圧は，1/3Vを初期値として，スイッチを切り替えるにつれてと1/4Vをはさんで上下し，1/4Vへと収束していきます．

かなり全体的にうそっぱちな説明をしてしまいましたが，いいたいことは理解していただいたようで安心しました．一度，切り替え３回目ぐらいまではしっかり計算されるのがよいでしょう．漸化式を導こうとされたくらいですから多分，もうすんでると思いますが．今のうちそうした遠回りをたくさんやっておくと，実戦でショートカットができるようになりますよ．

Yokkun さんのレス (2009/10/18(Sun) 11:57)

パソコンで計算してみたら，C2の電荷の移り変わりは，CVを単位として a) 2/3, 14/27, 122/243, 1094/2187・・・ b) 4/9, 40/81, 364/729, 3280/6561・・・ というぐあいです．一般項は， a) 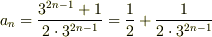b) 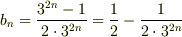となるようですね．

MEGAMAN さんのレス (2009/10/18(Sun) 18:20)

Yokkunさん，わざわざ計算までしていただいて本当にありがとうございます．

もう一度また訂正された文を読んでいき，理解を深めたいと思います．