遠心力

home > 掲示板 >

このページのPDF版

サイトマップ

遠心力

緋色さんの書込 (2009/10/12(Mon) 17:43)

はじめまして．緋色と言います．

学校で，「本当は自分たちが遠心力だと思っているものは遠心力では無い．遠心力は向心力に打ち消されるはずだから，本当の遠心力は見かけだけの力で慣性力の一種だ」と聞きました．最初は「バケツに水を入れて回した時に水が落ちてこないのは，向心力と遠心力が打ち消しあうからなのか」なんて納得してたのですが・・・．では私が遠心力だと思ってた物は何でしょうか？たとえば・・・車に乗っている時，カーブすると自分は外向きに引っ張られますよね？後は，コーヒーカップに乗っているときにも外側に引っ張られますし・・・．あれは，何なのでしょう？

わかりにくい文章ですみません；解答よろしくお願いします．

Re: 遠心力

ミュフ猫さんのレス (2009/10/12(Mon) 18:21)

人間が外力を感じることができるのは，体内に内部応力が生じるときです．つまり，細胞の隅々まで同じ外力が加わっても，その外力を実感できません．遠心力を感じるときは，体の接触物からの抗力が加わっているときだけです．座席やシートベルトから向心方向に抗力が加わるから，遠心力を自覚できるわけです．

Re: 遠心力

mNeji さんのレス (2009/10/12(Mon) 18:37)

緋色さん，難しい問題かも知れません．

私の個人的な意見を書いて見ます．

古典力学では，一定の速度で動いている座標系(静止座標系，慣性座標系)に対して運動方程式が建てられることは認めて頂けると思います．

回転系は，たとえ一定の角速度で回転しているとしても，加速座標系となってしまいます．従って，この加速座標系での振る舞いは，先ず適当な静止座標系で運動方程式を建てた上で，その静止座標系から考える加速座標系(この場合，回転座標系)への座標変換によって，加速座標系での運動方程式を得る訳です．

従って，静止座標系では回転の為の「向心力」によって軌道が曲げられていたのが，回転座標系では，向心力と遠心力とが釣り合うことによって，軌道半径が一定になっているようになる訳です．

私は，この「遠心力」というのは，「遠心項」とか「加速座標項」とすれば紛れがないように思います．実際，自動車とか電車の内部で「遠心項」は実在すると考えたほうが，直感的に運動を理解し易いからです．

他方，「慣性力」とか「見掛の力」という表現は，その言葉から間違った連想を引き起こすのではないかと思います．

どうやら，この問題の深い理解の為には，一般相対性理論と関連する様です．残念ながら，私はまだこの理解が出来ませんので，ご興味があれば他の方のご意見をお持ち下さい．

Re: 遠心力

Yokkun さんのレス (2009/10/12(Mon) 18:40)

>遠心力は向心力に打ち消されるはずだから，

これはちょっとちがうと思います．打ち消しあうから「見かけの力」であると考えるのなら，つりあう力はみな見かけになってしまいますよね．

「見かけの力」というのは，遠心力という力が，本来の運動の法則が成り立たない「非慣性系」からみたときに現れる力だからです．地上に静止する立場（慣性系）から見れば，車に乗った人もコーヒーカップに乗った人も，慣性によって直進しようとするために曲がって進む車やカップに押されるだけと観察されます．

Re: 遠心力

山旅人さんのレス (2009/10/13(Tue) 00:57)

>> mNeji さん > 回転座標系では，向心力と遠心力とが釣り合うことによって以前にもこの掲示板で議論したことがあるように， <b>向心力とは慣性系での概念，遠心力とは回転系（非慣性系）での概念</b> であって，この両者が <b>釣り合うなどということは有り得ない</b> のです．「大きさが等しく向きが逆」ということと「釣り合う」ということは全く別のことです．

緋色さんの学校の先生がいっておられる > 遠心力は向心力に打ち消されるはずだから，も，この誤解によるものです． Yokkun さんの見解を私も支持します．

Re: 遠心力

Yokkun さんのレス (2009/10/13(Tue) 08:45)

誤解のないように申し上げておきますが，mNejiさんと私の投稿はほとんど並行してなされたものであって，私はmNejiさんの議論に対して何か反論をしたということではありません．mNejiさんの議論は，質問者の方には難しすぎると思われますが，内容的には全く支持できるものです．

私自身は「この両者が釣り合うなどということは有り得ない」という立場には立てません．でも，山旅人さんの議論にはなるほどと同感できる部分があります．

本来「遠心力」自体も慣性系に片足をおきながら回転系に移った表現であると思います．ですから，私たちが向心力と遠心力とがつりあっているというとき，とうぜん慣性系から見た回転運動を知りつつなおかつ回転系に移って慣性力を含む力の関係を表現したということになります．「純粋な」回転系の立場は，回転によって生じた「重力」と車やカップからの抗力がつりあっているというものになります．「重力」の根源が回転にあることを知り得ない立場では，遠心力を含めなんの運動の記述もし得ないことになります．そこで私たちは，片足を慣性系においた半端な立場から，向心力と遠心力とのつりあいを考察することで，半径方向に運動がないことを説明しようとするわけですね．

ですから，こうした半端な立場をよしとしないmNejiさんの議論には，十分な意義があるものと考えます．また，認識論的にも慣性系と非慣性系とをはっきり区別しようとされる山旅人さんの議論についてもしかりです．

Re: 遠心力

mNeji さんのレス (2009/10/13(Tue) 12:18)

山旅人さん，

＞以前にもこの掲示板で議論したことがあるように，＞向心力とは慣性系での概念，遠心力とは回転系（非慣性系）での概念であって，この両者が釣り合うなどということは有り得ないのです．「大きさが等しく向きが逆」ということと「釣り合う」ということは全く別のことです．

「回転の向心力」は，回転中心に座標原点をもつ静止座標系で見ようが，回転座標系で見ようが，「同じ大きさと向きをもった力」であると思います．

例えば，地上の水平面上を等速回転運動中の車の中で，摩擦の無い水平面上に「おもりと糸」の系を静かに置き，乱雑な糸の端点をその摩擦の無い水平面上の一点Pに固定して，そのまま放置しておきます．

十分な時間がたてば，おもりは進行方向に垂直な方向ひっぱられて糸がピンとなるはずです．車の中の人は，車の回転運動によって出来た「遠心項(力)」と「糸の張力＝向心力」がバランスしたのだと解釈できるのではないでしょうか？

もし，「糸の張力」の最大値より「遠心項(力)」が大きくなれば，バランスが崩れておもりは飛び出すだけですね．

Re: 遠心力

ミュフ猫さんのレス (2009/10/13(Tue) 12:54)

等速円運動を強いられる観測者にとって，遠心力を感じるかどうかは，観測者の体に加わる向心力に偏りがあるかどうかで決まると思います．地球の周回軌道を進む宇宙ステーション内の乗組員は，等速円運動しているにもかかわらず，遠心力を感じません．つまり，たとえそれが引っ張り応力でも圧縮応力でも，体に内部応力が生じるときに，観測者は遠心力を実感します．よって，向心力が万有引力など観測者の体に一様に加わる力の場合，回転系では，局所的に遠心力と釣り合っている位置が存在すると言えるかもしれません．厳密には，万有引力も遠心力も一様な場を作らないので，大きさのある物体には僅かなりとも，内部応力が生じるわけですが・・・．

Re: 遠心力

mNeji さんのレス (2009/10/13(Tue) 13:01)

＞地球の周回軌道を進む宇宙ステーション内の乗組員は，等速円運動＞しているにもかかわらず，遠心力を感じません．

これは「遠心力」と「地球との重力」とが大雑把にバランスしているからでは無いでしょうか．

Re: 遠心力

ミュフ猫さんのレス (2009/10/13(Tue) 13:41)

>これは「遠心力」と「地球との重力」とが大雑把にバランスしているから >では無いでしょうか．

そう思います．地球の万有引力場に比べて，極めて狭い宇宙ステーションの船内空間に限って，大雑把にバランスしていると言えるかもしれません．

Re: 遠心力

山旅人さんのレス (2009/10/13(Tue) 21:41)

> これは「遠心力」と「地球との重力」とが大雑把にバランスしているからでは無いでしょうか．

言葉尻を捉えて揚げ足をとるつもりは毛頭ないのですが，遠心力とバランスしているのは地球・宇宙ステーション間の「万有引力」であって，重力ではないですね．万有引力と遠心力の差が重力で，バランスしているのですから差は 0，すなわち「無重力（空間）」ですね．

まあこのことは愛嬌だとしても，多くの方々が「遠心力と向心力の釣り合い」にさほどの違和感を感じられないということは，それだけこの問題が根深いということの証明でしょうか？それでも，ひととおり理解をされた方々にとっては害は少ないのでしょうが，高校生など初学者を混乱させる罪は大きいものがあります．これ以上混乱を深めないためにも，このような掲示板に回答を書かれる方々から改めて欲しいものだと思います．

再度ミュフ猫さんがあげられた例を引くと，感じないのは「遠心力」ではなく本来感じるはずの「地球の引力」であり，それを感じないのであるから「釣り合う力（＝遠心力）」を導入せざるを得ない，これが回転系での立場．静止系では，地球の引力が文字通り等速円運動の「向心力」になっている，紛れがないですね．

なぜ，不用意に「遠心力と向心力の釣り合い」などという表現をしなければならないのか，逆に私は理解に苦しみます．

Re: 遠心力

mNeji さんのレス (2009/10/13(Tue) 23:40)

山旅人さん，

No.25685 については，しばらく考えてから回答させて戴きます．元々のご質問者のかたの問から状況から乖離が大きいからです．

他方，「山旅人さんの No.25677 での論議についての私の疑問点」は No.25681にお書きしました．これに補足してみます．

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

少なくとも，回転座標系での動径成分の運動方程式；

運動量の時間変化＝向心力 + 遠心項(力)

ですが，動径方向の変化が無い，すなわち半径が一定なら，

０ = 向心力 + 遠心項(力)

と考えて良いと考えます．

この時の向心力は，静止座標系で見た時と同じヴェクタ量です．

Re: 遠心力

Yokkun さんのレス (2009/10/14(Wed) 01:17)

私は，山旅人さんのおっしゃる主旨を正確に捉えていなかったようです．

向心力＝円運動に必要な中心に向かう力

この呼称は，個別具体的な中心力の代名詞ではないということですね．「向心力と遠心力がつりあう」という表現は確かに気持ち悪いです．私は，「（向心力）と遠心力がつりあう」※（）の代わりに個別具体的な力が入るという代名詞的な用法で使ったつもりでしたが，確かに不用意でした．この表現を初学者が用いるとき，たいていマニュアル的な暗記に走っていて，ひどい場合には向心力を個別具体的な力と同一視したりすることがよくあります．

「向心力とは慣性系での概念，遠心力とは回転系（非慣性系）での概念」

本来の主旨で遅ればせながら，読解できたと思います．非慣性系で向心力という概念自体が成立しないのは当然です．

Re: 遠心力

mNeji さんのレス (2009/10/14(Wed) 04:41)

山旅人さん，

「向心力」という単語が，静止座標系，ないし等速運動座標系，ないし慣性座標系でのみ定義されたものであるという事を初めて伺いました．そのような定義ないしは概念の出典(図書，サイト等)をご教示下さると幸いです．または，より詳細な解説を書かれる事を期待します．

というのも，論議をする上で意見の相違は当たり前の事だと考えます．むし論議が噛み合ない原因を突き止めることによって正しい理解が得られると思うものです．その意味で，異論の生じている点を突き詰めて下さると幸いです．初心者の方から見ても，解り難いのではありませんか？

Re: 遠心力

mNeji さんのレス (2009/10/14(Wed) 13:16)

参考資料です．

念の為に，手持ちの「理化学辞典第3版」を見ましたので下記に引用します．

〜〜〜〜引用開始〜〜〜〜 <b>向心力(centripetal force)</b>

一様な円運動をする質点に働く力．円の中心に向かうのでこう名づける．

<b>遠心力(centrifugal force)</b>

慣性系に対し一定の角速度で回転する座標系に現れる見かけの力のうち，静止物体にも運動物体にも同じように働くもの．回転系で静止する物体では遠心力だけを考えればよい．[以下略] 〜〜〜〜引用終了〜〜〜〜

とあります．重要なのは，「向心力」には座標の制限が書かれていない点です．他方，【遠心力】については「慣性系に対し一定の角速度で回転する座標系に現れる」と明記されている事です．

また，Wikipediaで「centripetal force」を拝見すると「 http://en.wikipedia.org/wiki/Centripetal_force 」の冒頭にあるローラ・コースタの写真の左ほどに，次に引用する説明があります；

〜〜〜〜引用開始〜〜〜〜 Isaac Newton's description was: "A centripetal force is that by which bodies are drawn or impelled, or in any way tend, towards a point as to a center."[3] 〜〜〜〜引用終了〜〜〜〜

まだ，プリンキピアの原文はあたっていませんが，上の文の直ぐ前の文に；

〜〜〜〜引用開始〜〜〜〜 The term centripetal force comes from the Latin words centrum ("center") and petere ("tend towards", "aim at"), signifying that the force is directed inward toward the center of curvature of the path. 〜〜〜〜引用終了〜〜〜〜

とあります．恐らく，ニュートンさんが「向心力」と「遠心力」を対にして造語したのではありませんかね(私の推測)．

Re: 遠心力

Yokkun さんのレス (2009/10/14(Wed) 20:03)

日本語Wikipedia「回転運動」Http://ja.wikipedia.org/wiki/%E5%9B%9E%E8%BB%A2%E9%81%8B%E5%8B%95 では，

「このように，力が常に固定点の方向に向き，その大きさが固定点からの距離 r の関数である場合に，その力を向心力という．」

と表現していますが，これは中心力に近い解釈で，ちょっと首をかしげます．ただ，回転運動（円運動）とセットでの解説中の表現ですから，円運動に必要な力であることを前提としてはいるようです．

>一様な円運動をする質点に働く力．円の中心に向かうのでこう名づける．

等速円運動を継続させるのに必要な力であることを明記しています．そして向心力によって引き起こされる円運動の記述自体が，慣性系を前提としたものであることは，あえて言うまでもないこととして省略されているのではないでしょうか？非慣性系で円運動をする物体に必要な力は向心力にはなりません．

ともに回転する立場では，物体は静止しています．円運動としての記述もなければ，中心という概念すら出てはきません．

次の論文「Http://www8.plala.or.jp/stoneriver/ronbun/dalembert/index.html」の内容が私にはしっくりくる感じがします．向心力と「慣性抵抗」がつりあうとしたダランベールの原理は，慣性系の立場からのものであるという記述には「目からウロコ」でした．また，「遠心力に限らず一般に慣性力を考える場合には，物体とともに運動する観測者以外に慣性系の観測者の存在を暗黙の内に仮定する必要があるといえる．」という立場は，私が「慣性系に片足をおきながら」といったことに通じ，我田引水かもしれませんが，共感に値します．ぜひ皆さんにもご一読をいただきたいと存じます．

もちろん，「向心力と遠心力がつりあう」というとき，「向心力」は正確には「慣性系において向心力に相当している個別具体的な力」をさしているのであって，あげあし取りではないかと思われるむきもあるかもしれません．しかし，山旅人さんの主旨は，混乱を持ち込む余地のない教育的な表現に徹するべきであるとの戒めであると，私は読み取りました．この点につきましては，全く同感できるものです．

「遠心力」の用語としての歴史はわかりませんが，次の論文「Http://www.k4.dion.ne.jp/~ypc.suta/newskiji/ensinryoku.pdf」によりますと，プリンキピア以前にデカルトやホイヘンスにおいて遠心力概念に関する記述があるようです．勉強になりました．

さて，緋色さんの疑問をないがしろに大分寄り道してしまいましたことを反省しつつ，ひとまず引き下がります．

Re: 遠心力

山旅人さんのレス (2009/10/14(Wed) 21:06)

>> mNeji さん > 「向心力」という単語が … 慣性座標系でのみ定義されたものであるという … 概念の出典(図書，サイト等)をご教示下さると幸い

私も「慣性系のみで定義する」と限定した記述を見たことがあるわけではありません．しかし，非慣性系での考察の中で「向心力」という記述を書籍の中で見たこともありません．ましてや，「遠心力と向心力がつり合う」などという記述はこの掲示板でのみです．

「慣性系でのみ定義する」理由は，その定義からほとんど明らかです． > <b>向心力(centripetal force)</b> > 一様な円運動をする質点に働く力．円の中心に向かうのでこう名づける．(『理化学辞典第3版』）

質点とともに円運動をしている観測者（非慣性系）とってもはや質点は円運動をしていませんね．質点が円運動をしていることを知ることは難しいのです．

現実には，地球を周回するステーションの窓からは動く地球が見えますので，「自分が地球の周りを回っている」ことがわかります．しかし，このことは <b>静止系から回転する物体を見た経験からそのように判断できる</b> のであって，この経験がない人にとっては動いているのはどちらなのかわかりません．

つまり，自分が円運動をしていることを知っているのは，慣性系での経験（知識）を非慣性系内に持ち込んでいるからなのです．すなわち，非慣性系内で向心力を考えているのではなく，慣性系内で考えているに過ぎないのです．このような混同が不用意に行われると，初学者が混乱することは無理もないことでしょう．ですから，用語は限定的に用いるべきなのです．

（全く同趣旨のことは以前にも繰り返し申し上げたところでしたが…）

「向心力」でヒットしたいくつかのサイトを見てみましたが，

http://www8.plala.or.jp/stoneriver/ronbun/dalembert/index.html

などが，よくまとめられていると思います．尚，私は著者石川ではありません．

Re: 遠心力

山旅人さんのレス (2009/10/14(Wed) 21:12)

あら，Yokkun さんも同じサイトをご覧でしたか！！私も上記に Yokkun さんの「片足」を引用しようかと思っていたところでした．

Re: 遠心力

mNeji さんのレス (2009/10/15(Thu) 01:31)

山旅人さん，

＞私も「慣性系のみで定義する」と限定した記述を見たことがあるわけではありません．しかし，非慣性系での考察の中で「向心力」という記述を書籍の中で見たこともありません．ましてや，「遠心力と向心力がつり合う」などという記述はこの掲示板でのみです．

静止座標系で「向心力」の源が，荷電粒子に対する電気力とか磁気力(ローレンツの力)，重力，張力(糸，バネ)といった色々な場合について，回転運動を考える事があります．それを一般的に「向心力」と呼ぶのは至って自然だと思います．

それを，回転座標系で記述するときに「向心力」と呼んでも意味ははっきりしています．

＞質点とともに円運動をしている観測者（非慣性系）とってもはや質点は円運動をしていませんね．質点が円運動をしていることを知ることは難しいのです．

「難しい」と言う事は，原理的に知る事ができないとは違います．車に同乗している人が，「糸」と「錘」と「水平面」と「定規」と「鉛筆」をもって注意深く測定すれば，回転中心が進行方向に垂直で，どれだけ離れた所で有るかを確定出来ると思います．さらに外部の観測から，回転の角速度も測定出来ます．

それが出来ないというならば，では静止座標系(慣性系)にいる人は，どうして自分が静止座標系(慣性系)にいる事を簡単に知る事ができるのですか？

むしろ，「静止座標系(慣性系)」も「加速座標系(非慣性系)」も，同定するには同じ様に外部との関係の把握の結果として得られるのだと思います．

＞現実には，地球を周回するステーションの窓からは動く地球が見えますので，「自分が地球の周りを回っている」ことがわかります．しかし，このことは静止系から回転する物体を見た経験からそのように判断できるのであって，この経験がない人にとっては動いているのはどちらなのかわかりません．

まさに「古代の暦観測者から連綿とした経験，ガリレイさん，ケプラーさん，ニュートンさんの時代を経た」現代の知見をもっているのですから，「回転運動している加速座標系」にいる人が，自分の状況を把握しているとして良いと思います．

＞つまり，自分が円運動をしていることを知っているのは，慣性系での経験（知識）を非慣性系内に持ち込んでいるからなのです．すなわち，非慣性系内で向心力を考えているのではなく，慣性系内で考えているに過ぎないのです．このような混同が不用意に行われると，初学者が混乱することは無理もないことでしょう．ですから，用語は限定的に用いるべきなのです．

「向心力」は，正にその回転を生みだすもので，その力が回転運動を生みだしているわけです．それを回転座標系にいったから「向心力」と呼べないというのは，それこそ初心者にとって理解し難いものです．

もう一度，お聞きしますが，「静止座標系(慣性系)」で理想的な水平面上に大きなカプセルを置いて，理想的で適当な長さの糸により定点とつなぎ，定点の廻りに一定の角速度で回転運動を起こさせます．その動きは容易に単振動の解であることが判ります．

他方，それに乗った回転座標系からは，中心からの半径一定，ある座標軸からみた角度一定とみえますが，「自分の座標軸」が「外部の静止座標系(慣性系)軸」にたいして一定の角速度で回転する事を見いだして，静止座標系で得る運動方程式を座標変換して，自分の系での運動方程式を得る事ができる，と考えます．

＞「向心力」でヒットしたいくつかのサイトを見てみましたが，＞ http://www8.plala.or.jp/stoneriver/ronbun/dalembert/index.html ＞などが，よくまとめられていると思います．

これは，これから拝見してみます．

「などが」と有りますが，他の文献なり図書をご紹介願えませんか？

Re: 遠心力

mNeji さんのレス (2009/10/15(Thu) 11:31)

緋色さん，

私は，ご質問が「大学の一般物理」での授業についてであると思って回答をしてきました．でも「 http://www8.plala.or.jp/stoneriver/ronbun/dalembert/index.html 」を読み始めた所，「高校の物理」での授業についてであるような気がして来ました．実際の所，どちらの状況かお教え下さると，助かります．

Re: 遠心力

mNeji さんのレス (2009/10/15(Thu) 11:57)

山旅人さん，

ご案内戴いた「 http://www8.plala.or.jp/stoneriver/ronbun/dalembert/index.html 」を読み始めた所，ですが，これを基に論議の準備をするとかなり時間が掛かりそうです．

そこで私の大雑把な意見を述べます；

微分・積分の技量が少ない現状では，回転系の問題を高校で論ずるのは反対です．
加速座標系において，運動を理解する(運動方程式を立て，解く)には，静止座標系との幾何学的関係の理解を必要とする．

と思います．其の上で，

静止座標系で立てた運動方程式を，加速座標系に座標変換するという手続きを，常に念頭に置くできだと思います．この場合，座標変換した座標の時間微分から生じて来た項をもって，系の加速による項(いわゆる「見かけの力」；遠心項，コリオリ項，車等での急発進，急減速であらわれる系の加速項や減速項)と，静止座標系で認識出来る力(いわゆる「本当の力」)を明確に区別する能力が大切だと考えています．

取り急ぎ，中間意見とさせて戴きます．

Re: 遠心力

山旅人さんのレス (2009/10/15(Thu) 20:11)

多くを繰り返しません．上記のサイト「向心力，遠心力およびダランベールの原理」お読み下さったのなら，冒頭部分の

>なお，物体とともに等速円運動をしている観測者の立場で見るときは，“実際にはたらいている力"を“向心力"とは呼ばない．“向心力"とは，あくまでも等速円運動している物体にはたらいている力だからである．

もお読み下さったわけですね．これもお認め下さらないわけですね．いろいろ書きましたが，申し上げたいことはただひとつです． mNeji さんがお書きのとおり，

> 系の加速による項(いわゆる「見かけの力」…)と，静止座標系で認識出来る力(いわゆる「本当の力」)を明確に区別する能力が大切だ…

同感です．だからこそ，静止座標系の概念である「向心力」という用語を不用意に加速系での議論に持ち込まないでください．誤解と混乱を生むだけです．

Re: 遠心力

mNeji さんのレス (2009/10/16(Fri) 11:19)

山旅人さん，

昨日は所用が重なった上，スポーツ・ジムで運動のし過ぎをして考える時間がとれませんでしたので，まだ返答ができないので悪しからず．

＞>なお，物体とともに等速円運動をしている観測者の立場で見るときは，“実際にはたらいている力"を“向心力"とは呼ばない．“向心力"とは，あくまでも等速円運動している物体にはたらいている力だからである．＞＞もお読み下さったわけですね．これもお認め下さらないわけですね．

簡単には読みましたが，私の場合，頭の動きが遅いので，「読んだ」と「理解した」とには大きな乖離があります．確かに，現時点では「このサイトの方のお考え」も「山旅人さんのお考え」も私には理解できていません．しかし，このサイトの方が冒頭に示されている「現行の高校教育」に於ける「回転運動」の解説には高い抵抗を持つ者として，これから考察させていただきたいと思っております．

多くを繰り返しません．上記のサイト「向心力，遠心力およびダランベールの原理」お読み下さったのなら，冒頭部分の

>なお，物体とともに等速円運動をしている観測者の立場で見るときは，“実際にはたらいている力"を“向心力"とは呼ばない．“向心力"とは，あくまでも等速円運動している物体にはたらいている力だからである．

もお読み下さったわけですね．これもお認め下さらないわけですね．いろいろ書きましたが，申し上げたいことはただひとつです． mNeji さんがお書きのとおり，

＞> 系の加速による項(いわゆる「見かけの力」…)と，静止座標系で認識出来る力(いわゆる「本当の力」)を明確に区別する能力が大切だ…

＞同感です．だからこそ，静止座標系の概念である「向心力」という用語を不用意に加速系での議論に持ち込まないでください．誤解と混乱を生むだけです．

「同感です．」と仰る点に元気を戴きました．でも，その後の論点には，現時点では理解出来ません．あと数日は時間が掛かるだろうと思いますので，ご猶予ください．

ただし，今回の論議のなかでわかって来たのは，静止系と加速系との関係をさらに整理する必要を感じ出しています．ここら辺は，下手に私の論議を進めるよりも，昔読んだ力学の古典的名著でどうなっているかを確認したい所です．残念なことに，学生時代に集めた物理の本はほとんど手放してしまったので，時間が掛かりそうです．

うろ覚えですが，自分は（１）ゴールドスタイン，「古典力学」（２）山内，「一般力学」（３）ランダウ=リフシッツ，「力学」（４）ウィットタッカー，「解析力学」の原書などで勉強した筈なのですが．

もし，これらの図書を含めて「静止座標系の概念である「向心力」という用語を不用意に加速系での議論に持ち込んではいけない」という点を示している所をご存知でしたらお教え下さい．

Re: 遠心力

緋色さんのレス (2009/10/17(Sat) 00:13)

返信が遅くなってごめんなさい． Yokknさんの考えている通り，私は高校生です．

高校物理で習う遠心力をさらに大学で(より深く)習うなんて思ってもみなかったので，Yokknさんが私を大学生だと思われているとは気付きませんでした…．すみません．

ミュフ猫さんの＞人間が外力を感じることができるのは，体内に内部応力が生じるときです．つまり，細胞の隅々まで同じ外力が加わっても，その外力を実感できません．遠心力を感じるときは，体の接触物からの抗力が加わっているときだけです．座席やシートベルトから向心方向に抗力が加わるから，遠心力を自覚できるわけです．

や，Yokkenさんの＞「見かけの力」というのは，遠心力という力が，本来の運動の法則が成り立たない「非慣性系」からみたときに現れる力だからです．地上に静止する立場（慣性系）から見れば，車に乗った人もコーヒーカップに乗った人も，慣性によって直進しようとするために曲がって進む車やカップに押されるだけと観察されます．

という回答は，私にも理解出来たのですが，色々と私1人では理解出来ない内容の回答もあって…御礼を言うにしても，ちゃんと全て理解しなければ失礼だという思いと，皆様の前で言うのは恥ずかしい…というより恐れ多い気もしますが…私は物理が大好きですから理解したいという思いがあって(まだ物理のことも殆ど知らないのに生意気だとは自分でも思いますが)，皆様の回答を学校の先生に説明してもらっていました．とはいっても，今の私にも分るようになので昨日辺りからの討論はさっぱり分らないですが…

勘違いさせてしまって本当にごめんなさい．

Re: 遠心力

Yokkun さんのレス (2009/10/17(Sat) 10:38)

初めから，緋色さんが高校生であろうことは承知していました．

>皆様の回答を学校の先生に説明してもらっていました．

この掲示板をきっかけに先生に解説をお願いするのは，理解を深めるのによい手順ですね．

>ちゃんと全て理解しなければ失礼だという思いと，

そんなことはないんですよ．この場での議論は，緋色さんの質問をきっかけに，「向心力」という概念について盛り上がったわけですが，これはこれで大いに結構なことで私も楽しませてもらいました．ただ緋色さんへの回答から大分寄り道してしまったことはこちらの反省点です．「向心力」は円運動の理解には欠かせない大切な概念ですので，それをどうとらえるかで白熱したのです．緋色さんの質問で勘違いしたとかいうことは何もないので，安心してください．

Re: 遠心力

mNeji さんのレス (2009/10/17(Sat) 18:04)

山旅人さん，

ご紹介いただいた「石川昌司さんのサイト」を拝見しました．現在の高校の教科書の説明に納得できないという点は，大いに賛同します．でも，まだその説明は発展途上だと感じます．

自分が高校生のときも，当時(1963年ころ)の教科書で，教師の方と意見が衝突して，以後，教科書に依らず「PSSC物理」で勉強しました．従って，いまさら高校の教科書を読むのも嫌な位です．しかし，現在の高校の教科書を知らないで発言するのも如何と思い，手元にある高校学校・物理IIの２つの教科書； <pre> （１）兵藤申一／福岡登／他共著，新興出版社啓林館，平成18年12月10日発行．

円運動と単振動

（２）国友正和／他共著，数研出版，平成19年01月10日発行．円運動と万有引力 </pre> を拝見していると，私のような落ちこぼれには，驚くべき事が多すぎて，高校の物理の解説はできないように感じました．

やはり，回転運動を解り易くするには，「一定の糸の長さの先に錘を付けて一定の角速度でまわすような系」を静止系(x,y)で解き，次に座標変換した回転系(r,θ)で解く．という段階で遠心力の解釈をしていかないと駄目だろうと感じます．

他方，「回転系で向心力の概念は無い」とは，今だ理解出来ずにいます．気長に，「力学」の解説書にあたって検討を続けたいと思います．

以上の結果から，現時点では；「私は，高校学校・物理IIに沿って，回転系の解説をすることは出来ない．」と思うようになりました．

Re: 遠心力

mNeji さんのレス (2009/10/18(Sun) 12:54)

もう一度，高校の教科書を眺めて見ると，時間微分を隠して，いかにも物理的な理解だけを伝授するという，ある意味とても洗練された教育体系を構築するようにされていると感じます．

勿論，そのようなスマートな方法を受け入れる事ができる「先生・生徒」の皆様方は，それで幸いなのだと思えます．でも，これは小学生に代数学をわざと隠して，「鶴亀算」という「ある意味とても洗練された手法」を教え込むのと似ているように感じます．

やはり，回転運動を教えるなら，先ずは「糸と錘」で回転を自分の手で起こし，それをVTRで撮影し，大雑把に，回転半径が一定で，糸の張力が同じように感じる，といった所から入り，より詳しい実験を見せてやったり，静止系の微分方程式としての運動法式を立て，それを解く過程で一種の単振動として振舞う事を感じてもらうといった点を経験してから，回転系の運動方程式の有り難みも，その意味も解けないだろうと思えます．

類似した事が，電気回路の説明であり舞いした．コイルやコンデンサの過渡応答を微分方程式を隠したまま説明しても，消化不良のまま終わるのだと思います．

もはや高校でもPCを使った授業が可能だと思いますので，典型的な２階線形微分方程式までを高校の物理のなかで使えるように，物理・数学の教科全体を再構築するべきかと感じました．

高校・物理教育の落ちこぼれとしての意見でした．

Re: 遠心力

mNeji さんのレス (2009/10/23(Fri) 15:42)

山旅人さん，

時間が経ってしまいましたが，自分なりに「一定の長さの糸に付けた錘の回転」について，考えてみました．その計算ノートを下記に書いて見ました(未完)．

・「回転運動での向心力や遠心力の解釈」，2009/10/20(Tue) 15:10，No.25754

この結果，静止座標系(Oxy)で回転運動を導き出すのは面倒ですが，初心者さんが地表での重力場のなかで「塔から物を投げ出す」問題と比較して「回転運動」を理解する上で大切だと感じました．(以前，もっといい解法を拝見した気がするのですが，見つけ出せませんでした．)

＃逆に，幾何学的に加速度を運動形状の幾何学によって出すのは，＃むしろ極座標の解析を終えた後にする方が，判り易いと感じました．

他方，極座標表示への座標変換は，一般的な回転座標系の取り扱いの前に，明確にしておく方がいいと感じます．というか「極座標表示」は，一般的な回転座標系の特殊れいだと認識をしたほうが紛れ難いと思います．

さて，極座標表示では，原点Oからの動径距離 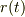r(t) と，x軸からの回転角 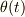$\theta(t)$ によって系を記述し，

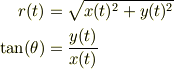
$r(t) &= \sqrt{x(t)^2+y(t)^2}\\\tan(\theta) &= \frac{y(t)}{x(t)}$

それに伴い，基底ヴェクトルとして単位直交ヴェクトル；

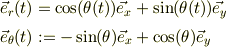
$\vec e_r(t) &= \cos(\theta(t))\vec e_x +\sin(\theta(t))\vec e_y \\\vec e_{\theta}(t) &:= -\sin(\theta)\vec e_x +\cos(\theta)\vec e_y$

によって，位置ヴェクタ 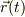$\vec r(t)$ ，質点に加わる力が純粋に向心力 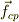$\vec f_{cp}$ である時には，これらが簡素に記述できる；

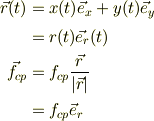
$\vec r(t) &= x(t)\vec e_x + y(t)\vec e_y &\\&= r(t)\vec e_r(t) \\\vec f_{cp} &= f_{cp}\frac{\vec r}{|\vec r|} &\\&= f_{cp}\vec e_r$

静止座標系で立てた運動方程式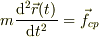； $m\frac{\mathrm{d}^2 \vec r(t)}{\mathrm{d} t^2} &= \vec f_{cp}$ から座標変換の結果，

動径方向について

$m(\ddot r -r\dot \theta^2) &= f_{cp} &\ ---(1)$

角度方向について

$\frac{\mathrm{d}(r^2\dot \theta)}{\mathrm{d} t} &= 0&\ ---(2)$

と二つの連立微分方程式となる訳でした．

式(2)は，角運動量が保存則を示しているのが味噌になる訳だと思います．そこで，角運動量 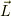$\vec L$ は；

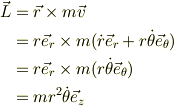
$\vec L&= \vec r \times m \vec v\\&= r \vec e_r \times m (\dot r \vec e_r + r \dot \theta \vec e_{\theta})\\&= r \vec e_r \times m (r \dot \theta \vec e_{\theta})\\&= mr^2 \dot \theta \vec e_z$

ですので，新たな積分定数として角運動量の大きさ;

$L &:= mr^2 \dot \theta &\ ---(3)$

とすると，式(1)を整理して下記直すと；

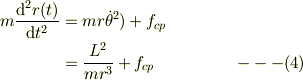
$m\frac{\mathrm{d}^2 r(t)}{\mathrm{d} t^2}&= mr\dot \theta^2) + f_{cp}\\&= \frac{L^2}{mr^3} + f_{cp} &\ ---(4)$

もし向心力が動径距離だけの関数なら，

$f_cp &= F_{cp}(r) &\ ---(5)$

ならば，動径方向の変数の従う微分方程式は，角度依存性を持たないので，この回転座標系だけの観測量でみで記述できる；

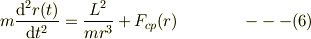
$m\frac{\mathrm{d}^2 r(t)}{\mathrm{d} t^2}&= \frac{L^2}{mr^3} + F_{cp}(r) &\ ---(6)$

もし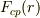， $F_{cp}(r)$ の関数形が与えられれば，その解も時間の関数としてられます．

＃この時，この力は保存力になりますね．またこの力を，中心力と呼ぶ事もありますね．＃中心力は，向心力に含まれる概念です．

でも初期条件も含めて解を用とすると，式(3)を含めて計算する必要が生じてくるので，角度の情報，言い換えれば，静止座標系から見た情報がないといけないのだとおもいます．

他方，中心力の関数形，初期条件が決まって，円運動の解が許される場合は，その時の半径 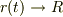$r(t) \to R$ について，

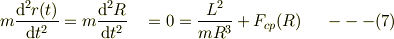
$m\frac{\mathrm{d}^2 r(t)}{\mathrm{d} t^2}&= m\frac{\mathrm{d}^2 R}{\mathrm{d} t^2}&= 0&= \frac{L^2}{mR^3} + F_{cp}(R) &\ ---(7)$

という意味で，遠心項(力)と求心力(中心力)の和はゼロとなってバランスすると言えると思います．この時にも式(3)が成立していることから，角速度 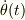$\dot \theta(t)$ も一定である事になります．

＃本当は，仕事の積分を持ち込めば，説明は直感的になると思いますが，サボります．

〜〜〜〜〜以上から，私見としては，現状の高校教科書では；

「回転運動を教える事は，弊害が多すぎるので止めるべき」

と考えます．

折角，若い頭脳が発展中の高校〜大学というゴールデン・エイジに，中途半端な説明をするのは止めて，高校生の段階から，系統的に「微積分，複素数，ヴェクタ解析」を教え，直交座標系での運動を身につけてから，極座標系に進み回転運動を取り扱うようにするほうが，学ぶ側も教える側も納得出来るだけでなく，効率も高いのではありませんか？

高校での授業経験が豊富な方々のご意見をお聴きしたいところです．

Re: 遠心力

mNeji さんのレス (2009/11/07(Sat) 18:59)

ｍさん，

＞向心力なるものは応力と（本質で）どう違うのでしょう．さっぱり分かりません．

向心力の具体例を上げるとすれば，２電荷間のクーロンの力，２質点間の万有重力，一定の磁束密度の場に垂直に運動する電荷に掛かるローレンツ力などが思い浮かびます．

これらと応力(単位面積当りの力)とを直接に比較するのはどういう観点からなのでしょうか？

[home] [掲示板] [ページの先頭]