藍猫 さんの書込 (2009/10/11(Sun) 15:13)

始めまして藍猫です 私と私の研究パートナーはテニスにおいて，デッドスポット（ネットの一番下の方）（以下DS)，COP，NODE（スイートスポット）の三点にボールが衝突した時，どのような違いが生まれるかを実験しようと思いました． 理論上，それぞれの実験（DS，COP，NODE)で同じ力をラケットに加えた場合NODEがテニスボールに対して一番運動エネルギーを送れると仮説しました．

しかし，実験方法に問題がありました． 私の実験では，ラケットの下から3.5cmほどの所に長細い棒を差し，そこを中心点としてラケットを回転させると言うものでした．この回転の際，ラケットは90度の角度まで上げられ，そのまま手を離すことで自然と重力に引っ張られ棒を中心軸とし回転する事で必然的に同じ量の運動エネルギーが生まれるはずでした．（この３回の実験の際，DS,COP,NODEに静止したボールが当たるようにしました） しかし翌々考えてみると，DS,COP,NODEはネット上の位置がそれぞれ違うのですから，回転運動をする際にそれぞれ違う量の運動エネルギーが生じる事になります．

（以下ウィキペディアのトルク参照） 回転運動の場合 KE=(1/2)Iω^2 が運動エネルギーですから I=ma^2+MA^2 そして ω＝v/r で運動エネルギーは求まる筈ですよね？

しかしネット上の，それぞれ別の位置にあるDS,COP，NODEが持つ運動エネルギーに対してこの計算は有効なんですか？

Yokkun さんのレス (2009/10/12(Mon) 07:32)

こんにちは．

>それぞれ別の位置にあるDS,COP，NODEが持つ運動エネルギーに対してこの計算は有効なんですか？

KE=(1/2)Iω^2は，ラケット全体の回転のエネルギーです．

>DS,COP，NODEが持つ運動エネルギー

お気持ちはわかりますが，剛体のある1点がもつ運動エネルギーというのは定義できません．明らかなのは，3点において衝突速度が異なるということですね？

藍猫 さんのレス (2009/10/13(Tue) 03:39)

>>Yokkunさん お返事ありがとうございます！

＞KE=(1/2)Iω^2は，ラケット全体の回転のエネルギーです． やはりそうですか・・・

＞剛体のある1点がもつ運動エネルギーというのは定義できません．明らかなのは，3点において衝突速度が異なるということですね？ つまり全体は分かるが，特定の点は分からない・・・と言う事ですね． はい，明らかなのは衝突速度が違うと言う事だけです．観測したデータでは回転軸から最も外側にあるDSが一番衝突速度が大きいと言う結果になりました．

Yokkun さんのレス (2009/10/13(Tue) 09:04)

>つまり全体は分かるが，特定の点は分からない・・・と言う事ですね．

分かる，分からないという問題ではなく，定義できるかどうか，意味をなすかどうかという問題です．１点がもつ速度は意味をなしますが，１点がもつ運動エネルギーというのは何をいっているのか意味不明です．運動エネルギーについて重大な誤解があるのではないかと疑われます．

>観測したデータでは回転軸から最も外側にあるDSが一番衝突速度が大きいと言う結果になりました．

「衝突速度」とは，ボールの飛び出し速度のことでしょうか？ 衝突速度が半径に比例して大きくなるのは純粋に幾何学的な問題で，まったくあたりまえですよね？カギは，ラケットの衝突点の衝突直前の速さと，ボールの飛び出し速さとの比較にあると思います．いわば，その打点における反発係数ですね．この反発係数を２つの速さから計測することが，すなわちエネルギー伝達の効率を測定したということになると思います．ただし，現実には反発係数自体は，衝突速度の大きさによって変わるということは念頭に置くべきと思います．

また，「衝撃の中心」という問題も考察されたらよいのではないかと思いました． ttp://www.geocities.jp/eulers_formula/mechanics10.html

藍猫 さんのレス (2009/10/14(Wed) 04:36)

＞１点がもつ速度は意味をなしますが，１点がもつ運動エネルギーというのは何をいっているのか意味不明です． 一点が保つ運動エネルギーと言う，言い方が間違ってました．すみません 一点が保つ速度をKE=1/2mv^2に当てはめて運動エネルギーを計算出来ないか・・・と言う意味です このサイトの一番上の画像 ttp://www.physics.usyd.edu.au/~cross/tennis.html 此所にあるDead spot, node, COPのそれぞれの場所にボールを衝突させるんですが． 先日話した方法でラケットをボールと衝突させる時，dead spotが一番速度が速いですよね？ その場合，その速度を計算する方法はありますか？

＞「衝突速度」とは，ボールの飛び出し速度のことでしょうか？ そうですね，静止状態にあるボール（速度＝0m/s）が速度を保つラケットと衝突した時，ボールが飛び出す速度の事を言いたかったんです． エネルギー伝達率は エネルギー伝達率in％＝（ボールの運動エネルギー/ラケットの運動エネルギー）×100 で良いんですか？（慣性抵抗は存在するが，無視した状態で）

ラケットの衝撃の中心はCOPですね．Center of percussion（衝撃の中心）の略称です

Yokkun さんのレス (2009/10/14(Wed) 08:46)

ご紹介いただいたサイトはなかなかおもしろそうですね．

>その場合，その速度を計算する方法はありますか？

ボールの飛び出し速さはどう測定されているのですか？落下の水平距離かな？ もし光ゲートとかで直接測定されているのならば，ラケットについてもどこか１点の速さが測定できれば，v=rωから任意の点の速さが計算できますよね？

慣性モーメントを実体振り子の微小振動の周期測定などから計算して，衝突時のωを理論的に求めることは可能ですが，もし速さが直接測定できるのならその方がいいのではないでしょうか？

何かの分野の専門的なものとしてでなければ，「エネルギー伝達率」なる量を基礎力学上できちんと定義されたものを私は知りません．したがって，ここでは目的に見合う定義をされればよいのだろうと思います．その上で，提示された定義は計算可能なものの中では妥当なものではないでしょうか．また，このように定義された場合の「伝達率」は反発係数で一意に決まりますので，衝突前後の相対速さの比で決定すると思います．もちろん，実戦上の相対速さはかなり大きく，反発係数も低速度での実験とは異なることが予想されますが，低速度での反発係数に関する限り，水平に固定したラケットにボールを落として，はねかえる高さを測定してもよいわけですよね．

ご紹介の実験の場合，回転軸での力については考察し得ない内容だと思いますが，一方「衝撃の中心」について考えるとは，そのことも考えるという意味で，手からラケット，そしてボールへ・・・という伝達の効率を考察することに値すると思います．ご紹介の実験は，とりあえず手始めとしては，もちろん有意義な実験だと思いますが，どこで打つのがよくとぶか，という総合問題を解くものとしては十分でないような気がします．その辺は私もよくわかりませんが．

藍猫 さんのレス (2009/10/15(Thu) 06:57)

＞ボールの飛び出し速さはどう測定されているのですか？落下の水平距離かな？ 飛び出し速度の計算は実に曖昧だと思いますが， Logger Pro ttp://www.vernier.com/soft/lp.html と言うソフトウェアを使いました． このソフトウェアは，録画した実験ビデオを取り込み「弾道」に関する要素を計算する為の物です． （このプログラムでは速度はX線上とY線上しか分からないので，ピタゴラスの定理を使い，v=√(x^2+y^2)としました） 録画したビデオをこのソフトウェアに取り込み，テニスラケットがボールと衝突し，ボールが飛び出して行った直後のXとY速度を使い，vを導き出しました．（直後と言うのは0.1秒以下です．しかしこのプログラムでまともな観測結果が得られない様な気がして成らない・・・）

＞実体振り子の微小振動の周期測定などから計算して これはどのような計算なんでしょうか？ お手数ですが教えて頂ければ嬉しいです

＞また，このように定義された場合の「伝達率」は反発係数で一意に決まりますので，衝突前後の相対速さの比で決定すると思います． なるほど． 反発係数を使用した伝達率

Yokkun さんのレス (2009/10/15(Thu) 12:14)

Logger Proなるほど，おもしろそうですね． そうすると，ラケットの衝突前後の速さも測定できそうですね．

「実体振り子」で検索すると出てくるとは思いますが， Http://www.hepl.phys.nagoya-u.ac.jp/~ohshima.nagoya/d03/d03-18.pdf などが参考になります．

1. ラケットおよびボールの衝突前後の速さを測定する．
2. ラケットを回転軸で鉛直にぶらさげ，わずかに振らせて周期を測定する．
3. 周期からラケットの慣性モーメントIを計算する．
4. 衝突直前のラケットの速さから角速度ωを求めると，ラケットの運動エネルギーはE_0 = 1/2・Iω^2
5. 衝突直後のボールの速さから運動エネルギー E_1 = 1/2・mv^2を求める．
6. 先の定義による伝達率は，α = E_1/E_0
7. おまけとして，衝突直後のラケットの運動エネルギーをE_2とすると，?E = E_0-E_1-E_2はわずかにプラスになり，衝突時のエネルギー損失を表す．

こんなんでどうでしょうか？

藍猫 さんのレス (2009/10/15(Thu) 22:23)

なるほど，実体振り子ですか

1，4〜7は分かるんですが（とても良いアイデアです！有り難うございます 2と3が良く分からないんです・・・ つまりラケットを，静止状態から一定角度φ持ち上げて T(周期)=2π√(I/Mgh) T^2=4π^2 * I/Mgh T^2/4π^2=I/Mgh (T^2/4π^2)*Mgh=I I=(T^2/4π^2)*Mgh

と言った風に求めるのでしょうか？・・・ そうなるとT＝周期と言うのは，つまり10秒間にラケットが何回一周するかを求めるんですか？

毎度，毎度質問ばかりですみません・・・

Yokkun さんのレス (2009/10/16(Fri) 08:29)

計算はあってます．

周期は，実体振り子としての微小振動の周期ですから，

実験と同じ回転軸でラケットを鉛直に下げ，ちょっとつついて小さく（といっても十分振動が持続する程度）振らして，その周期を求めればいいのです．往復で１周期（正確には鉛直線を右向きに切ってから，再び右向きに切るまでの時間）ですからお間違えのないように．１０秒ではちょっと物足りないかな？数十秒カウントして，時間を振動回数で割ればいいのですね．時間を決めてしまうより，５０回なり１００回といった振動回数を決めておいて，その所要時間をはかった方が正確になります．

藍猫 さんのレス (2009/10/16(Fri) 08:30)

えっと，この事について私とパートナーは先生に「この計算は正しいのか？」と聞いたところ．ノーが帰ってきました

先生が言うには，位置エネルギーと運動エネルギー（直進運動の）だけで計算できるだろ？と言われました． 先生の計算は ラケット９０度の状態にある時位置エネルギーが働き，ラケットを放し，ボールと衝突する瞬間には運動エネルギーに変わるといわれました． つまり， PE＝mgh の状態でこの位から， KE＝(1/2)mv^2 を差し引けばいいだろうと言われました

しかしこの計算は間違っていると思うんです． 今回の場合ラケットが円運動をしているので，直進運動の計算は使われない筈ですよね？ しかもこの運動エネルギーの場合，ラケットそれぞれの点の速度を考慮していないと思うんです．

先生に対して失礼なのはわかりますが，納得出来ない以上引けないのです

先生と抗議した内容は私は「円運動である以上，その計算は成り立たない」といいました． しかし先生は「位置エネルギーと運動エネルギー（直進運動の）で計算できる」の一点張りです

この場合私が間違っているんでしょうか？それとも先生が間違っているんでしょうか？ たびたびの質問誠に申し訳ありません．

Yokkun さんのレス (2009/10/16(Fri) 11:44)

先生の説明を誤解されているのではないでしょうか？

おそらく，先生は運動エネルギーは位置エネルギーの減少分だから，

mgh = 1/2・Iω^2（ただし，hは重心の落下の高さ）

になるということをいいたかったのでは？だから，「伝達率」の分母は，重心が落下する高さから計算すればすむといいたかったのでしょう．

私はなぜ，1/2・Iω^2を持ち出したかというと，ボールの飛び出し速度が水平でないようなお話でしたから（カメラが傾いていた？），衝突点は最下点でないのではないかと疑ったからです．ラケットの初期位置が水平で，衝突点が最下点であることが保証されているのならば，何も1/2・Iω^2の計算をする必要はないのです．

藍猫さんがおっしゃることは，その通りで，最下点でのラケットの重心の速さを 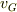とすれば，

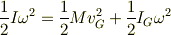
が成り立ちます．なお，ここで 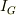は重心まわりの慣性モーメントです． つまり， ラケットの運動エネルギー＝重心運動のエネルギー＋重心まわりの回転エネルギー となるわけです．

藍猫 さんのレス (2009/10/16(Fri) 16:32)

どうやら私の誤解＋先生の仮定があったからの用です 色々疑問がありましたが，遂に理解する事が出来ました． あんなに霧が掛かっていたように訳が分からなかった事も，今はハッキリ理解出来ます． これもYokkun様の回答のお陰です． 本当に有り難うございました！