一周するとVだけ電圧降下するわけ
一周するとVだけ電圧降下するわけ
ｍｋ さんの書込 (2009/10/01(Thu) 16:44)
こんにちは．
電気について勉強していて不思議に思ったのですが，一周すると電源がVだった場合Vだけ電圧降下するのは何故なのでしょうか．
よく川（？）のようなもので例えられますが，これは電子の動きでは説明できないのでしょうか．
よろしくお願いします．
Re: 一周するとVだけ電圧降下するわけ
Yokkun さんのレス (2009/10/01(Thu) 18:36)
うーん．いざ説明するとなると，難しいですね． 電圧というものをどうとらえているかに深く関わってきます．
電圧＝電位差は，まさに電位の差であり，電位＝電場のポテンシャルは， 「その場に電荷が存在するとき，単位電気量あたりにもつ電気力による位置エネルギー」 という意味をもちます．
したがって，水流モデルで電流を考えるときに，電位は高さに対応させることができるのです．ポンプで高い位置に持ち上げられた水は，重力による位置エネルギーを持ちますが，それは高さに比例します．同じように，電源は（正）電荷を電位の高い所に持ち上げて（実際には負電荷をもつ電子を電位の低い所＝位置エネルギーの高い所に移動させて）,すなわち電荷が持つ電気力による位置エネルギーを高めます．電気抵抗などの負荷をつないで回路にしてやると，導体中の電場によって電気力を受けた電子が移動する際に，ジュール熱などとなってその位置エネルギーが消費されるわけです．水流モデルでは，よく水車などにたとえられますね？
水路をぐるっとめぐって，初めの高さに流れ落ちた水は，重力による位置エネルギーを失ってゼロにもどる．同様に，回路をぐるっとめぐって，初めの電位にもどった正の電荷（実際は逆にめぐってもどった電子）は電気力による位置エネルギーを失ってゼロにもどると理解できます．
Re: 一周するとVだけ電圧降下するわけ
リモコン さんのレス (2009/10/01(Thu) 23:39)
電池と抵抗の回路を考えてみます． 電池が起電力を持つということは，電子は電池内部において非クーロン電場を受けて加速されているということです． 加速されているということは，電子の速度がどんどん増していきます． その時，電池が電子にした仕事（を電気量で割ったもの）が起電力になります．
一方，抵抗内部では，電子は速度に比例した力を受けます．よって，速度が増していくと，その分抵抗内部で電子が受ける力も増してきますので，電池が電子に作用させている力と，抵抗力が釣り合ったところで，電子の速度は一定となります． （※空気抵抗があるときの物体の落下運動の様子をイメージしてみて下さい．物体は終端速度に達した後，等速運動をしますよね．） その時，抵抗力が電子にした仕事（を電気量で割ったもの）（抵抗力は電子の運動する向きと反対向きの力なので，負の仕事をします）が，（電圧降下）をマイナス倍したものになります．
電子の速度が今，一定で，電子は電池，及び抵抗からのみしか，仕事をされていませんから， （電子が受けた仕事の総和）＝０ （起電力）−（電圧降下）＝０ （起電力）＝（電圧降下） となります．
オームの法則とは，抵抗内部では，電子が，まるで空気抵抗を受けた運動のように，結果的にはある一定の等速運動になる（定常電流になる）．という主張です．
コンデンサについては， 「導体に定常電流が流れる問題」と「帯電した誘電体コンデンサの問題」は数学的取扱が同じです．（ちょっと前にぶどうさんが投稿した記事『RC=ρεの導出』，記事No.25270が関係しています．参考にして下さい．） 具体的な対応関係は
（抵抗率）×（電流）⇔（電気量）／（誘電率） です．
数式を利用しない，汚い文になってしまい，すみません． もし，私の考え方に誤りがあったら，ご指摘お願いします．
Re: 一周するとVだけ電圧降下するわけ
mNeji さんのレス (2009/10/03(Sat) 03:21)
リモコンさん，横から失礼します．一部についてコメントをさせて下さい．
＞（起電力）＝（電圧降下） ＞となります． ＞オームの法則とは，抵抗内部では，電子が，まるで空気抵抗を受けた運動のように，結果的にはある一定の等速運動になる（定常電流になる）．という主張です．
この部分の考え方は解り易いと思います．さらに，起電力が加えられた回路について，「一定の電場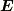 
」が生じていて，この電場と電流密度 
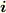について微分形のオームの法則，
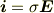
が成立すると考えておくとイメージが明確になるように思いますが，如何ですか？
【追伸】 「電流の連続性」と「電場の線積分が，電源の起電力に等しくなる事」とを明示的にしておくべきだと思いました．
