波動方程式

波動方程式

sweetdays さんの書込 (2009/09/28(Mon) 00:41)

こんばんは，sweetdaysです． 波動方程式を変数分離法で解くにあたり，まず分離定数をzeroと置いたときを考えています．このとき，境界条件はu(o,t)=X(x)T(t)=0, u(l,t)=X(l)T(t)=0になると思うのですが，書籍に，時間の関数T(t)はすべてのtについてzeroにはならない，と書いてありました．これはどうしてでしょうか？漠然とはわかるような気がするのですが，きちんと理解できていない状況で，色々と調べてみたのですがよくわかりませんでした． 解説していただけるとありがたいです．よろしくお願いします．

Re: 波動方程式

mNeji さんのレス (2009/09/28(Mon) 10:54)

＞時間の関数T(t)はすべてのtについてzeroにはならない

これはどういう事を仰りたいのでしょうか？

例えば，固定された２点間にはられた弦に波動を生じさせることを考えます．一番考え易くする為に，何処かの一点に変位を与えて波動が開始させることはできます．

ところが，何も強制的に変位を与えたり，速度を与えなければ，弦は未来永劫に静止していませんか？

なにかご質問の主旨と違い過ぎていたら，ごめんなさい．

Re: 波動方程式

sweetdays さんのレス (2009/09/29(Tue) 16:05)

mNejiさん，返信ありがとうございます．

>何も強制的に変位を与えたり，速度を与えなければ，弦は未来永劫に静止していませんか？

これは理解できるのですが，これと，時間の関数T(t)がすべてのtについてzeroにはならない，とはどのように関係しているのでしょうか？

Re: 波動方程式

mNeji さんのレス (2009/09/30(Wed) 03:20)

前にも書きましたが，

＞時間の関数T(t)がすべてのtについてzeroにはならない

の部分を，その解説に従って書き出して頂ければ検討します．

Re: 波動方程式

sweetdays さんのレス (2009/10/05(Mon) 02:49)

mNejiさん，返信が遅れて本当に申し訳ございません．ここ数日体調を崩しており，書き込むことができませんでした．心よりお詫びいたします．どうかご容赦ください．

本題ですが，以下，書籍に記載されている内容を記します．

分離定数をzeroと仮定すると，位置の関数および時間の関数は次のように表される． X(x)=ax+b T(t)=cx+d X(x)とT(t)の場合，境界条件はu(0,t)=X(x)T(t)=0, u(l,t)=X(l)T(t)=0である． T(t)がすべてのtについてzeroにはならないので，X(0)=0およびX(l)=0でなければならない．

これ以上のことは書いてありませんでした．

また，改めて図書館の本を見たところ，X(x)を波の形，T(t)を波の全体的な高さ，と解釈している本がありましたが，そう考えてもT(t)がすべてのtについてzeroにはならない理由が見いだせませんでした．理解不足で申し訳ありません．

Re: 波動方程式

mNeji さんのレス (2009/10/05(Mon) 10:15)

状況は判りました．ただ，私は微分方程式の深い理解をしていないので，上手く説明出来るかどうか...，しばし考えさせてください．

なお上で，T(t)=ct+d ですね．

＞X(x)を波の形，T(t)を波の全体的な高さ

という説明は初めて拝見しました．興味深いです．

〜〜〜〜 微分方程式が得意の方がいらっしゃったら，助言を戴けると幸いです．

Re: 波動方程式

sweetdays さんのレス (2009/10/05(Mon) 22:08)

>T(t)=ct+d タイプミスでした．すみません．

お時間あるときでかまいませんので，恐れ入りますがよろしくお願いします．

Re: 波動方程式

mNeji さんのレス (2009/10/06(Tue) 19:14)

ご質問を勘違いしていました．

先にも申し上げましたが私は数学が苦手なので，書籍を引用して説明します．

ついては，熱伝導の方程式を変数分離で解きたいというご質問「一次元熱伝導方程式について，光太郎さん No.25208」の論議も参考になるかも知れません．

そこで引用した図書；

理工系の基礎数学 ４， 偏微分方程式， 及川 正行・著， 岩波書店， ISBN4-00-007974-3

この「第２章波動方程式，2.2節 フーリエの方法」の「弦の自由振動」の説明のの先頭部分を引用しますと；

〜〜〜〜引用開始〜〜〜〜〜〜 <b>弦の自由振動</b>

次のような両端固定の弦の自由振動を考える．

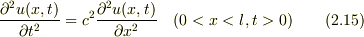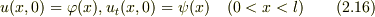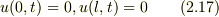
(波動方程式) ： \frac{\partial^2 u(x,t)}{\partial t^2} = c^2 \frac{\partial^2 u(x,t)}{\partial x^2} \quad (0 <x <l, t>0) \qquad (2.15) 初期条件： u(x,0) = \varphi(x),u_{t}(x,0) = \psi(x) \quad (0<x<l) \qquad (2.16) 境界条件： u(0,t) = 0, u(l,t) = 0 \qquad (2.17)

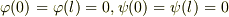ただし， \varphi(0)= \varphi(l)=0, \psi(0)=\psi(l)=0 とする．

（途中略）

この分離乗数 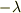-\lambda とおくと，2つの常微分方程式

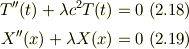
T''(t) +\lambda c^2 T(t) =0 &\ (2.18)\\X''(x) +\lambda X(x)= 0 &\ (2.19)

を得る．

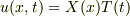u(x,t) = X(x)T(t) が境界条件(2.17)を満たすということから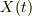， X(t) が境界条件

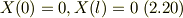
X(0)=0, X(l)=0 &\ (2.20)

を満たす事を要請しよう．

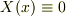X(x) \equiv 0 は明らかに(2.19),(2.20)の解であるが，これは役に立たない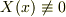． X(x) \not\equiv 0 の解を求めたい．次の３つの場合に分けて考える．

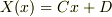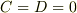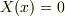(i) 分離乗数=0. このとき(2.19)の一般解は \ X(x) = Cx +D であって，(2.20)から C=D=0 となり， X(x)=0 となってしまう．

（以下略） 〜〜〜〜引用終了〜〜〜〜〜〜

という説明のようです．明示的に式(2.20)を与えたのが味噌でしょうかね．

Re: 波動方程式

sweetdays さんのレス (2009/10/12(Mon) 09:57)

返信が遅くなり申し訳ありません．引用していただいた文献をきちんと読んでから返信したく，遅くなってしまいました（昨日ようやく図書館でみることができました）． 私自身，勘違いというか，難しく考えて混乱していたようです．少しだけすっきりしました．私が参照している書籍にはtに関する条件や初期条件については触れられていなかったのですが，t>0であれば納得だと思います．というのも，t=0のときはまだ弦に振動を与えていないので，u(0,t)=X(0)T(t)=0において，t=0のとき，T(0)=0でもよいのではないかと考えた訳です． mNejiさん，本当にありがとうございます．

Re: 波動方程式

mNeji さんのレス (2009/10/12(Mon) 13:03)

＞私自身，勘違いというか，難しく考えて混乱していたようです．少しだけすっきりしました．

これを拝見して，ほっとしました．

＞（昨日ようやく図書館でみることができました）．

このシリーズは，とても味のある解説だと感じています．私は若い頃『数学は使えればいいのだと割り切っていた』のですが，このサイトを知ってから，数学の大切さを身に沁みて感じました．その経験から，物理数学の入門書をいろいろ探しているのですが，今の所，このシリーズのバランスの良さ，説明の直裁さ，などは他の類似書に比較しても抜き出ている様に思います．