無題
無題
オメガ さんの書込 (2009/09/16(Wed) 13:58)
こんにちは.オメガです.
すみません,昨日投稿した問題を,誤って削除されてしまいました. 自分のレスのコメントだけを削除したつもりだったのが,レスのコメントからボタンで入ったのですが,全部削除されてしまったようです.
私はもう,解決しました.みなさん,ありがとうございました.
他の方が,まだ話で盛り上がっている途中でしたので,すみませんです.
Re: 無題
mNeji さんのレス (2009/09/16(Wed) 14:34)
>まだ話で盛り上がっている途中でしたので,
私は,まだ頭の中で考え中ですよ(笑).
初めは,式無しで説明するのは難しいなあ,と思いながら考えているうちに,仮に式を使った場合,「錘の動き」と「お猿さんの動き」との関係をどうやって表現すればいいのかが「?」の状態にいます.
確かに,この問題は,通常の問題と何かが違う様ですが,私はまだ理解し切れていません.
#現在は,天井から吊るした紐をお猿さんがよじ登ることは理解出来そうです. #これは,固定した相手に紐をつけて,紐を手繰り寄せる操作ですね. #次に,理想的な滑車をつけて....
でも,面白い問題を知ることが出来たことを感謝します.
Re: 無題
ぶどう さんのレス (2009/09/17(Thu) 02:19)
あらら,消えちゃったんですか. 私もかぎしっぽ初心者で,ときどきこの掲示板の操作は迷うことがあります. Mneji様の英語の原文のサイトまでは拝見しましたが,その後も盛んな議論があったようですね.
またの質問でお会いできることを楽しみにしております.
Re: 無題
ぶどう さんのレス (2009/09/17(Thu) 02:22)
mNeji様 先ほどのレスで名前を間違えてしまい,失礼しました. パスワードを設定しておらず修正できないこと,お詫び申し上げます.
Re: 無題
mNeji さんのレス (2009/09/17(Thu) 09:05)
ぶどうさん,
>先ほどのレスで名前を間違えてしまい,失礼しました. >パスワードを設定しておらず修正できないこと,お詫び申し上げます.
ご心配無用です.解り難いHNでご免なさい.
ぶどうさんの論議も面白そうだったので,ゆっくり読むつもりでしたが残念です.
Re: 無題
mNeji さんのレス (2009/09/18(Fri) 14:00)
まだ理解出来ていないと思うのですが,すこし論議を進めてみたいと思います.
一番始めに気になったのは,自力で「自分を引き上げる」の所でした.池に船を二艘浮かべてひもで引き合うのと同じですが....これは取り敢えず,天井のある一点Fから固定部を引き下ろし,その固定点Oからロープを垂らし,そのロープにお猿さん(M)が手と足とを交互に伸び縮みを繰り返して,自分を引き上げると思う事にしました.
<pre> 図1天井に対して固定された点Oからのロープを登るお猿さん
■■■■■■■■■■■天井 ■ ■ ■ ーーー+ーーーーーー■O || ↓張力 T || || |手/| ||↑推進力 T = 張力 ・X_M □ 胴 ||/足↓重力 mg | | |地面 ーーーーーーーーーーーーーーーーーーーーーーーー </pre>
このお猿さんの運動は,
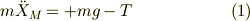
次に,滑車(半径a,慣性能率I)を介して同じ質量の錘(S)と理想的な紐(重さ無し,伸びも無し)で結ばれているとします.この段階で引っかかったのは,滑車が理想的だと,滑車に発生するトルクがバランスする事で,系が動けなくならないかという点でした.結局この点を説明する為には式を立てる必要があると思いました.
で,降参して下記の様にしてみました.
<pre> 図2天井に対して固定された点Oに滑車をつけて,「おもり」と「お猿さん」が紐で連結
■■■■■■■■■■■天井 ■ ■滑車の回転角θは反時計回りとする
A ■ B
ーーー+ーーーーーーー・・・ | 張力T_S↓ |O|↓張力 T | || | || | |手/| | ||↑推進力 T = 張力 ・X_M |□ 胴 | ||↓重力 mg | 張力T_S↑ | |/足 ・X_S ○ |
- 重力mg↓ おもり |
- | | | |
|地面 ーーーーーーーーーーーーーーーーーーーーーーーー </pre>
おもり,お猿さん,滑車の運動方程式は;
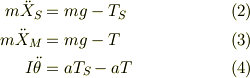
さらに,紐は滑車と滑らずに動く仮定を入れて

式(4),(5)から滑車の回転角度  を錘の変位
を錘の変位 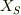 に替えると,
に替えると,
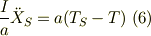
これに,式(2),(3)により 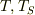 を消去すると,
を消去すると,
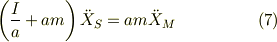
という線形な関係が保たれることが判ります.慣性能率が「 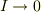 」の極限で,錘とお猿さんは等加速を受けますし,当然,錘に掛かる張力は,お猿さんの出す推進力に等しくなります.
」の極限で,錘とお猿さんは等加速を受けますし,当然,錘に掛かる張力は,お猿さんの出す推進力に等しくなります.
〜〜〜〜 中間結果です.
もともとの問題では滑車の慣性能率を無視するようですが,式から追う場合,有限の慣性能率から出発した方が,考え易いと思います.
ただ,自分には,このような問題を式無しで説明出来るとは思えません.どうすれば,そのような事ができるのか知りたいです.
Re: 無題
mNeji さんのレス (2009/09/22(Tue) 09:37)
その後,式の意味を考えていたのですが,結局,滑車の慣性能率を無視するということは,滑車廻りのトルク・バランスを要請していることだと思い至りました.
この点は,多くの方もそのように考えられると思いますが,其の結果,「滑車が廻らない」という点で困られたのだと思います.自分もその一人で,其の為に,有限の慣性能率から始めると考えた次第です.
でも,「おもり」は紐の端点と固定されていますが,「お猿さん」は紐の端点と「手」か「足」のどちらかが固定されながら移動している訳です.いいかえれば,「おもり」と「紐」はおなじ運動をしますが,「お猿さん」はその「紐」に対して上昇運動していると考えれば良いのではないでしょうか.
〜〜〜〜 前回の論議で見つけたサイトがみつからなかったので,「Lewis Carroll Monkey puzzle」で検索していたら,
・The monkey on the Rope
がありました.文章だけで説明しているようです.ご参考まで.
#なお,その下の方を良く見ると,さらに説明があるようです....
【追伸】
元のスレッドで,「Scientific American」で論議がなされたような記述があったと思うのですが,それを見つける事ができませんでした.もしご存知でしたら出典をお教え下されば,幸いです.
Re: 無題
Yokkun さんのレス (2009/09/22(Tue) 13:12)
ロープの質量を考えた場合も  においては,滑車の慣性を考えた場合と同様に,おもりとともにひとつの運動方程式にまとめることができますから,猿の運動方程式と比較すると結果的に初期状態においておもりの加速度と猿の加速度が同符号であるという結論(mNejiさんの(7)にあたる)を得ます.この場合,猿が大きくなっていく力で引き続けるというほとんど不可能なことをしない限り,力を弱めた時点でたぐりよせられたロープの重みによって,いずれ下降に転じて落ちていくことになります.
においては,滑車の慣性を考えた場合と同様に,おもりとともにひとつの運動方程式にまとめることができますから,猿の運動方程式と比較すると結果的に初期状態においておもりの加速度と猿の加速度が同符号であるという結論(mNejiさんの(7)にあたる)を得ます.この場合,猿が大きくなっていく力で引き続けるというほとんど不可能なことをしない限り,力を弱めた時点でたぐりよせられたロープの重みによって,いずれ下降に転じて落ちていくことになります.
猿は上に昇りたければ,力を弱めて降りていこうとすればよかったのだというおもしろい結果を得ます.そうすれば,ロープはおもり側に繰り出されてその重みで猿は上昇に転じ,つかまっているだけで上に昇ることができるわけです.
Re: 無題
mNeji さんのレス (2009/09/23(Wed) 09:32)
Yokkunさん,
>ロープの質量を考えた場合も (略) この場合,猿が大きくなっていく力で引き続けるというほとんど不可能なことをしない限り,力を弱めた時点でたぐりよせられたロープの重みによって,いずれ下降に転じて落ちていくことになります.
問題を改変された論議ですから,本文と関係がないと思いますが,誤解を受ける可能性があるのでコメントします.
「紐の取り扱いは面倒な所がある」とは思います.でも「理想的な紐」を考えるのは,初心者が物理に馴染んでいく過程で大切な事だと思います.
さて,この問題では「紐は理想的である」というだけしか書いていない様ですが,私は,この紐を有限な長さの輪だと考えたら良いとおもいます.これなら,紐の質量は,「おもり」側でも「お猿さん」側でもほぼバランスするとおもいますし,紐の運動方程式も容易に書けます.
>猿は上に昇りたければ,力を弱めて降りていこうとすればよかったのだというおもしろい結果を得ます.そうすれば,ロープはおもり側に繰り出されてその重みで猿は上昇に転じ,つかまっているだけで上に昇ることができるわけです.
これは何をいわれているのでしょうか?皆目検討が付きません.ボートから岸に紐を投げて,岸に紐の端点を固定して,ボートの人が紐をいくら操作しても, ・岸に近づくことは可能, ・岸から遠ざかることは不可能. これは,紐は張力しかでないので,引力の伝達はできても,斥力の伝達は出来ない事に由来します.
お猿さんは紐をつたって上昇するか,せいぜい紐につかまって重力に引き降ろされるのを防ぐしかありません.推進力が重力にまければ,加速度は確実に地上の方向を向いて下降するしかない,と思います.
Re: 無題
Yokkun さんのレス (2009/09/23(Wed) 12:03)
mNejiさん,レスありがとうございました.
>問題を改変された論議ですから,
mNejiさんもご存知のとおり,もともとの原典には「ロープおよび滑車の質量を無視する」といったような条件は書いてなかったように思います.「理想的な紐」というのも何をもって理想的とするかは謎ですね(私だったら「伸び縮みしない」と読みますが).ですから,あとに続いたパズルマニアがこれらの条件を付け加えて解きやすくした改訂版も出回っています.
両者の質量を無視した場合(そして張力の原理を認めた場合)は,猿・おもりともに常に同じ速さで上昇するというのが正解だと思います.両者の慣性を考慮するのは面倒なので,ロープの質量だけ考慮してみます.
猿とおもりの質量を  ,ロープの質量を
,ロープの質量を  とします.
また,猿側の張力を
とします.
また,猿側の張力を 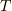 ,おもり側を
,おもり側を 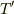 とします.
猿およびおもりの加速度を上向きに
とします.
猿およびおもりの加速度を上向きに 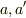 とおいて,
とおいて,  の瞬間の運動方程式を猿,おもり,ロープの順序でたてると
の瞬間の運動方程式を猿,おもり,ロープの順序でたてると
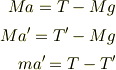
となります.3式から,
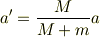
を得ます.これがmNejiさんの(7)に相当する関係です. これによって,両者の初期加速度は符号が同じであるという結果を得ます. 猿はロープを引くわけですから,いずれの加速度も上向きです.
すると,ロープは猿の方にたぐり寄せられますから,猿が余分にきたロープの重みに負けないように増大する力で引き続ける・・・という無茶ができない限り,いずれ下降に転ずることになります.
初期条件を変えて,猿がロープを引く力を弱めて下降しようとすれば,両者の初期加速度はともに下向きになり,ロープはおもり側に動きます.その後,ロープを引く力を大きくして,ロープの上の同位置にとどまるだけで猿は上昇に転ずることになります.この事情は,滑車の慣性を考慮した場合も同様です.
原典の問題の自由度はかなり高いものとなっています.そこで,おそらくルイス・キャロルもサム・ロイドも(ひょっとしてガードナーも?)いろいろと悩んだのではないでしょうか? してみれば,このような「改変」は結果のおもしろさもある有意義なものとして,許されると存じます.
蛇足ですが,挿絵(サム・ロイドの著作のものでしょうか?)のロープは輪にはなっておらず,原典にあるリンゴと,ゆさぶっている様子が描かれています.だからといって,mNejiさんの滑車の慣性を考慮した議論も,私のロープの質量を考慮した議論も決して無駄なものではなく,ともに有意義な「改変」であることに変わりはありません.
Re: 無題
mNeji さんのレス (2009/09/23(Wed) 12:19)
>mNejiさんもご存知のとおり,もともとの原典には「ロープおよび滑車の質量を無視する」といったような条件は書いてなかったように思います.「理想的な紐」というのも何をもって理想的とするかは謎ですね(私だったら「伸び縮みしない」と読みますが).ですから,あとに続いたパズルマニアがこれらの条件を付け加えて解きやすくした改訂版も出回っています.
私は,「もともとの原典」が何なのかを含めて,その内容さえもまだ確認出来ていません.でも,幾つかのサイトから予想出来そうなのは,シンプルな問題だと言う事です.
#著作権は,十分に切れている様な気もしますが....
>「理想的な紐」というのも何をもって理想的とするかは謎ですね(私だったら「伸び縮みしない」と読みますが).
確かに難しいかもしれませんが,初学者の方々に細かな精密論をするのも行き過ぎだと思います.
「おもりに理想的な紐を付けて回転させる」と考えられるからこそ,回転運動を理解出来るのだろうと思います.その後に,質量をいれたり,伸びをいれたり,エネルギー損失をいれたり,伝搬速度を考えたり....
いずれにしろ,この手の問題を精密に論議するのは別途のスレッドで,ご存分になされると良いかと思われます.
Re: 無題
anon さんのレス (2009/09/25(Fri) 00:27)
前のスレッドでは少し言葉が過ぎたようで,反省しています. 私のコメントでお気を悪くされた方がいたとしたら,ごめんなさい.
前のスレッドのオメガさんのコメントを読んで,, 返信しようと思った矢先にスレッドごと消えてしまったのと, 連休でアクセスできずにいたのが重なってそのままになっていました. その後,いろいろ盛り上がっているようで良かったですね.