黒体放射の式について
黒体放射の式について
sweetdays さんの書込 (2009/09/08(Tue) 18:31)
こんばんは.sweetdaysと申します. 今,プランクが導いた黒体放射の式を勉強しています.この式を振動数で表したものから波長表現にする場合,dν=(-cdλ/λ^2)という関係を用いればよいと思うのですが,そうすると式にはマイナスが入ってきます.しかし,書籍を見たところ,その式にマイナスはありませんでした.その理由として,「dν and dλ have opposite signs.」と書いてあったのですが,この解釈がよくわかりません.解説願えませんでしょうか. 宜しくお願い致します.
Re: 黒体放射の式について
Yokkun さんのレス (2009/09/08(Tue) 18:59)
こんばんは.
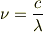
より,
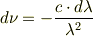
というわけですね. 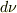 と
と 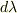 の符号が異なりますので,
の符号が異なりますので,  が増加すれば,
が増加すれば,  は減少.そこであらためて変化の絶対値をとって
は減少.そこであらためて変化の絶対値をとって 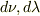 (初めの定義では
(初めの定義では 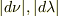 )の関係を示したということではないでしょうか?
波長の増加分(減少分)を
)の関係を示したということではないでしょうか?
波長の増加分(減少分)を 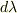 ,振動数の減少分(増加分)を
,振動数の減少分(増加分)を 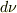 と定義しなおして,
と定義しなおして,
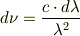
と負号をとりのぞいたというわけでしょう.
Re: 黒体放射の式について
sweetdays さんのレス (2009/09/09(Wed) 00:36)
Yokkunさん,早速有り難うございます. >あらためて変化の絶対値をとって という部分がよくわからないのですが,λの増減に対してνのそれは逆になるということ(つまり本来どちらかに符号がつく)まで含めて各々の微小変化を定義し直している,ということでしょうか? 丁寧に解説して頂いたにもかかわらずものわかりが悪くてすみません.
Re: 黒体放射の式について
mNeji さんのレス (2009/09/09(Wed) 02:10)
横から失礼します.
始めの  に関する積分の下限 と上限は振動数の小さな値から大きな値になっているとおもいます.振動数を波長にするという事は,変数の書き換え
に関する積分の下限 と上限は振動数の小さな値から大きな値になっているとおもいます.振動数を波長にするという事は,変数の書き換え  をする訳ですね.当然,
をする訳ですね.当然,  の 積分の下限と上限も対応して変わり,波長の長い所から波長の短い所への積分になる筈です.従って,
の 積分の下限と上限も対応して変わり,波長の長い所から波長の短い所への積分になる筈です.従って, 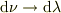 で符号が変わっても,積分域の逆転があれば,積分結果とすれば符号は反転しないのだと思います.
で符号が変わっても,積分域の逆転があれば,積分結果とすれば符号は反転しないのだと思います.
Re: 黒体放射の式について
Yokkun さんのレス (2009/09/09(Wed) 08:31)
たとえば,  が増加するとき,
が増加するとき,  が減少しますよね?
本来の変化の定義では,
が減少しますよね?
本来の変化の定義では, 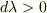 のとき,
のとき, 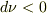 です.
この場合に,振動数は「どれだけ変わったか」と問うとき
です.
この場合に,振動数は「どれだけ変わったか」と問うとき 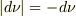 だけ減ったといいます.減少量を絶対値で示したいという目的から,変化の絶対値を改めて
だけ減ったといいます.減少量を絶対値で示したいという目的から,変化の絶対値を改めて 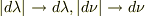 と置き直したにすぎないと私は思ったのですが.
と置き直したにすぎないと私は思ったのですが.
Re: 黒体放射の式について
sweetdays さんのレス (2009/09/10(Thu) 22:07)
Yokkunさん,ご説明有り難うございました.また,mNejiさんも解説有り難うございました.これからも精進して学んでいきたいと思います.お二方に感謝申し上げます.