雪崩
雪崩
あん さんの書込 (2009/09/08(Tue) 08:03)
助けて下さい.雪崩の問題が解けません.
水平とαの角をなす斜面に一様に積もった雪が上部から次々に積み重なりながら落ちるときの雪崩の加速度を求めよ.
という問題です.よろしくお願いします!
Re: 雪崩
mNeji さんのレス (2009/09/08(Tue) 08:58)
回答出来る訳ではありませんが,雪崩のモデルをどう考えるかが判らない限り,コメント出来ない様に思えます.
例えば,
(1)初期状態として,どのように雪崩がおこるか. (2)「ずり落ちる幅」のような概念があるとか, (3)重なり合った場合,回転を考慮するとか, (4)静止している雪の摩擦係数? (5)重なって来た雪と,下の雪の関係?
等々が必要なきもしますが,どうなんでしょうね?
Re: 雪崩
あん さんのレス (2009/09/08(Tue) 09:24)
私もその通りだと思います.が,問題文がこれしかなくかろうじて答えが 加速度a=gsinα/3 ということが分かっています. 何か方法はないでしょうか…
Re: 雪崩
mNeji さんのレス (2009/09/08(Tue) 11:52)
>加速度a=gsinα/3
何か簡単な近似を考えられているのかもしれませんね.
単に斜面と言えば; ・面に垂直な方向の重力成分,A=gcos(α) ・面に平行な方向の重力成分,B=gsin(α)
ですから,ほっといてもBの加速を受ける筈が,その2/3倍だけ抑制されているといった感じですね.
#ひょっとすると,摩擦なぞはあまり影響しないのでしょうか?
>何か方法はないでしょうか…
・その前後の問題や解説文をジックリみるとか? ・その出題者の方に質問してみるとか? ・スイスとか雪崩の多い国のサイトを探してみるとか.
Re: 雪崩
Yokkun さんのレス (2009/09/08(Tue) 14:24)
係数が1/2となる,単純化モデルならみつかったのですが,1/3となると3乗の微分の係数でしょうか? それとも三角形の重心位置? 力学的エネルギーが保存するモデルと思われますので,積み重なり方の問題かなあ?
以下,1/2のモデルです.
斜面に沿って原点から下向きに  軸をとります.
雪の密度を
軸をとります.
雪の密度を  ,雪崩によって落ちていく積雪の断面積を
,雪崩によって落ちていく積雪の断面積を  とします.
雪崩が
とします.
雪崩が 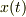 まで進んだとき,そこまでの巻き込まれた雪の体積は
まで進んだとき,そこまでの巻き込まれた雪の体積は 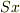 です.
この体積がすべて
です.
この体積がすべて  の位置で
の位置で 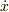 の速さを持っていると単純化すると,エネルギー保存により
の速さを持っていると単純化すると,エネルギー保存により
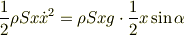
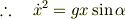
時間微分をとって,
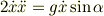
これから,加速度を求めると
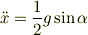
となります.
Re: 雪崩
Yokkun さんのレス (2009/09/08(Tue) 17:17)
雪の厚さや幅にかかわらず一定の加速度を要求されていて, なおかつ,雪塊の大きさが無視できる極限では 明らかにエネルギー保存を満足しない結果と思われますので, 雪塊と巻き込まれる雪との衝突・合体を考えればいいのかなあ ・・・と,毎度の思いつきです.質量が時間とともに変化する 点で何かロケット方程式のような感じになりそうな気がします.
Re: 雪崩
yama さんのレス (2009/09/08(Tue) 17:25)
確かに力学的エネルギーが保存するかどうかが問題ですね.
回転しないで単純に滑り下りる場合は,非弾性衝突的に雪をくっつけながら滑り下りるので力学的エネルギーは保存しないと思います.
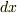 だけ滑り下りるときにくっつく雪の質量は
だけ滑り下りるときにくっつく雪の質量は 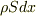 なので,このときの速度変化を
なので,このときの速度変化を 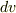 とすると次の式が成り立ちます.
とすると次の式が成り立ちます.
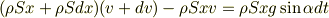
左辺は運動量の変化で,右辺は重力の力積です.摩擦力は無視しています. これを整理すると
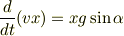
となり
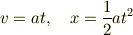
で表される等加速度運動であると仮定すると
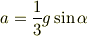
が得られます.
回転がある場合は力学的エネルギーが保存するモデルも可能です. カーペットを巻き取るように転がり下りるわけです. 円柱の慣性モーメントを考慮した力学的エネルギー保存の式から
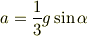
が導かれます.ただし,雪の厚さは無視できるものとします.
Re: 雪崩
Yokkun さんのレス (2009/09/08(Tue) 18:43)
帰宅途中の車中で解いてみたのですが,先をこされたようです.>yamaさん
後半の巻き取りモデルもおもしろそうですね. 前者の合体による力学的エネルギー損失分が,後者の回転の運動エネルギーにちょうど相等するというところがびっくりです.運動量−力積関係からあたりまえなのかな?
細かくて恐縮ですが,  が抜けてましたね.^^;
が抜けてましたね.^^;
Re: 雪崩
yama さんのレス (2009/09/08(Tue) 20:51)
御指摘ありがとうございました.訂正しておきました.