たろう（学部2年） さんの書込 (2009/09/07(Mon) 23:12)

どうも初めまして．このサイトに掲載されている群論の項目について いくつかわからない点があるので質問させていただきます．

「群の同型」という項目でじゃんけん，給食，１の３乗根を掛ける操作，３で割り切れる数字に１を足す操作などが例として挙げられていますが 例えばじゃんけんなどを群として見た場合「何が元」で「何が演算」なのか よくわからなくなります． グー，チョキ，パーが元なら演算は「じゃんけんをすること」なのでしょうか？ しかしそれならばその演算の結果生ずる元とはいったい何なのでしょうか？ それと単位元についても「じゃんけんをしない」とあってまるで演算そのものが 群の元であるように言われていてかなり頭が混乱しています．

ほかの例についても何が元で何が演算なのか解説していただけるとありがたいです．

ぶどう（学部4年） さんのレス (2009/09/08(Tue) 15:07)

群論は選択授業で半期だけでとったことがある程度ですので，あまり自信はありません．間違っていたらどなたかご指摘お願いします．

正直私も「じゃんけん」の例は理解できていません．そもそもどのように定義しているのでしょうか．直感的な定義では（グーとチョキに対し，「じゃんけんで勝つ」演算を施すと，グーになる）としたいのですが，そうなると群とはいえなくなります．

まず，代数系｛{グー，チョキ，パー，じゃんけんをしない}，じゃんけんで勝つ｝は群ではありません． 結合法則が成り立たないからです． 例――― 式?＝じゃんけんで勝つ｛（じゃんけんで勝つ｛チョキ，グー｝），パー｝ ＝じゃんけんで勝つ｛グー，パー｝＝パー

式?＝じゃんけんで勝つ｛チョキ，（じゃんけんで勝つ｛グー，パー｝）｝ ＝じゃんけんで勝つ｛チョキ，パー｝＝チョキ

よって式?≠式?より結合法則は成り立たない．この代数系は群ではない． ―――― その他の条件を見ていきましょう（あまり意味のないことですが．） 代数系｛{グー，チョキ，パー，じゃんけんをしない}，じゃんけんで勝つ｝の元[じゃんけんをしない]を単位元とするということは， じゃんけんで勝つ｛グー，じゃんけんをしない｝＝グー （チョキ，パーに関しても同様） が成り立つことを意味します．つまり「出さなきゃ負けよ」という意味でしょう． じゃんけんに結合法則がない以上単位元を定義する意味も分からないですが…．

さらに，逆元はどのように定義するのでしょうか？ じゃんけんで勝つ｛グー，○○｝＝じゃんけんをしない

じゃんけんで勝つ｛グー，グー｝＝じゃんけんをしない（グーの逆元はグー） と定義すれば，代数系が閉じていることはなりたちます． じゃんけんで勝つ｛グー，パー｝＝パー であり，[じゃんけんをしない]も[パー]もじゃんけんの元ですから代数系は閉じています．

anon さんのレス (2009/09/08(Tue) 17:03)

件の解説を読んでみました．

おそらく，どの例も， 「３つの要素を持つ集合上の置換群の，ある特定の変換によって生成される部分群」 の例になっていて， どれも位数３の巡回群であるというようなことだと思います． そう考えれば，単位元の説明ともよくマッチするようです．

ぶどう さんのレス (2009/09/08(Tue) 17:43)

所用があって学校に来たので，当時使っていた教科書より追記します．

ごめんなさい，さきほど「代数系は閉じている」といいましたが，「閉じている事」が代数系の条件でした．じゃんけんの集合{グー，チョキ，パー，じゃんけんしない}が演算(じゃんけんに勝つ)について閉じているので代数系と言える，と訂正いたします．

「情報の基礎離散数学―演習を中心とした―，小倉久和著，近代科学社」 を引用すると， 『2つのグラフの接点を1対1で対応させるが全単射あって，そのとき辺もうまく対応しているならば，その全単射はグラフの隣接関係を保存するという．』 『隣接関係を保存する全単射が存在する２つのグラフは互いに同型であるといい，そのような写像を同型写像と言う．』

ここでは群や単位元を問いませんので，じゃんけんを「3を法とする剰余類に1を足す操作」と同型と言えます．（対応が分からなくなるので元[じゃんけんをしない]を定義しません．）

集合{グー，チョキ，パー}から集合{グー，チョキ，パー}への対応 グー→チョキ，チョキ→パー，パー→グー は，全単射となる．

集合{0,1,2}から集合{0,1,2}への対応 0→1，1→2，2→0 は全単射となる．

ここで例えば，グー→0，チョキ→1，パー→2と対応させると上の二つの写像は同型写像であることが分かります．給食や三乗根の例でも同じ事がいえることが分かると思います． なお，剰余類は加法に対して群です．このときの単位元は零元0となります． 集合{1, (-1+√3i)/2，(-1-√3i)/2}は乗法に対して群です．このときの単位元は1となります．

ぶどう さんのレス (2009/09/09(Wed) 00:06)

anon様，助け舟ありがとうございます． じゃんけんの元をグー，チョキ，パーとおいたのが間違いでしたね．

確認ですが，この場合の集合 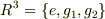の元は グーをＧ，チョキをＣ，パーをＰとおくと， （tex数式中に全角文字を入れられないため頭文字を使いました．eは単位元[なにもしない]を表します．）

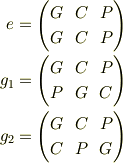
で演算はこれら置換の積ということでよろしいでしょうか．

anon さんのレス (2009/09/09(Wed) 09:04)

件の解説からどうにかして同型な群の例を読み取ろうとするなら， ぶどうさんのNo.25518のように解釈することになると思います．

件の解説は用語の使い方が曖昧なので， よほど群論に明るくないと読み取るのは難しいでしょうね． 執筆なさった方の書き直しを期待します．

ただ，位数３の巡回群の日常的な例を即興で挙げろと云われたら， 私でも，とっさにこんな言い方になってしまうというのはありそうです． 講義でこれをやってしまうと， 学生の反応の悪さに準備不足を後悔することになります．

ぶどう さんのレス (2009/09/09(Wed) 15:08)

ありがとうございました．