イーさん さんの書込 (2009/09/05(Sat) 18:15)

「ニュートンのゆりかご」と呼ばれる，球が５つくらいぶら下がっていて，カチカチ衝突する玩具？の運動について教えて下さい．

片側から１個ぶつけると逆側に１個，２個ぶつけると逆に２個はじける．分かる気がします．

そこで，今回は５つ球が連なっているとして考えます． 片側から３個ぶつけると，逆に残った２個だけでなく，真ん中の１個もついて行って，３個はじけます．残りの２個が１．５倍はじけても良さそうなのに…

今度は片側から２個，逆側から１個を同時にぶつけてみると，２個ぶつけた反対側で２個，１個ぶつけた反対側で１個はじけます．１個分のエネルギーが真ん中で打ち消しあって，１個だけがはじけたりしないのは何でなんでしょうか？

個人的に調べてみて，運動量保存則であるとか，完全弾性衝突のようなことが関係あるような気がしますが，イマイチよく分かりません．

理科系に関しては全く素人なので，数式などは全く分かりませんので，分かりやすい言葉で解説していただけるとありがたいです． 宜しくお願いします．

toorisugari no Hiro さんのレス (2009/09/05(Sat) 20:25)

> 数式などは全く分かりませんので，分かりやすい言葉で解説していただけるとありがたいです．

数式を使わない説明は私には無理なので，数式を使います．

弾性衝突なので，エネルギー保存則と運動量保存則を両方とも満足する運動しか実現しません．

質量 の物体が速度 で動いているとき， 運動量は 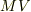エネルギーは 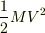になります．

複数の物体が運動しているときは，エネルギーも運動量もそれぞれの粒子の和で考えます．

例えば，3個の同じ物体がかたまって動いているとき，運動量は3倍の 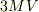，エネルギーも3倍の 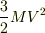です．

(総和の)エネルギーと(総和の)運動量が衝突の前後で等しくなければいけないというのが，エネルギー保存則と運動量保存則というわけです．

> 片側から３個ぶつけると，逆に残った２個だけでなく，真ん中の１個もついて行って，３個はじけます．残りの２個が１．５倍はじけても良さそうなのに…

簡単のため 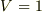とします．残りの2個の物体がそれぞれ速度 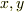ではじけたとすると，エネルギー保存則と運動量保存則から

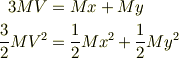
つまり

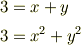
を満たさなければいけません．しかし， を消去した式

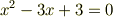
は実数解を持ちません．つまり，解はありません．

「残りの２個」だけではどうしても二つの保存則を共に満たすことができないので，3個がはじける事になります．

# ちなみに片側から2個ぶつけると，「残りの２個」の速度は

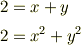
を満たさなければいけません．このときは 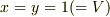となります．

Yokkun さんのレス (2009/09/05(Sat) 20:55)

物理的に何が起こっているか，私なりに補足してみます．

実は2個をテープで一体化して衝突させると，2個飛び出すという現象は起こらず，止まる球はひとつもなく，全部がばらばらになって前進する結果が得られます．十円玉のおはじきでも実験できますのでやってみてください．もちろん，これも運動量保存とエネルギー保存で説明できます．

toorisugari no Hiroさんは，衝突させた球が静止する事を前提として数学的に明快な説明をされました． 私も，目からウロコでした．

でも物理的，初歩的にはこの「静止」は必ずしも自明ではないようです．実はよく知られていることではありますが，「ニュートンのゆりかご」でｎ個ぶつけてｎ個飛び出す現象は，球の中を弾性波が有限の時間で伝わることによる1個1個の連続衝突と考えないと説明がつきません．完全弾性衝突では，２球の衝突では完全に速度が交換することが示されます．おはじき状態ですね．これが「静止」の原因です．

○->○ ○○ ○○->

そして，たとえば３個のときは

○->○○ ○○○ ○○->○ ○○○ ○○○->

わかりやすく球をたがいに離して描きましたが，弾性波が伝わるのに時間がかかるので，接触した球でも同じになるわけです．２個ぶつける場合も，２個がタッチの差で別々に衝突すると考えると，わかると思います．

>１個分のエネルギーが真ん中で打ち消しあって，１個だけがはじけたりしないのは何でなんでしょうか？

これは，基本的には「波の独立性」によって説明されます．弾性波は，途中ぶつかって重ね合いが生じても，通り過ぎれば何事もなかったように通り過ぎるためと考えればよいのではないでしょうか？

mNeji さんのレス (2009/09/05(Sat) 21:06)

＞数式などは全く分かりませんので，分かりやすい言葉で解説して

これが一番難しい質問かもせ入れません．

自分でも式を立てて計算しては居ないのですが，恐らく味噌は，「衝突する２つの玉ごとの完全弾性衝突が，数珠つなぎに起こる」のだろうと思います．

簡単な例を考えますと；

<pre> 図１２つの衝突

(1-1) →・ 速さ ○●

ＡＢ 玉の名；Ａが，静止中のＢに接近

〜〜〜〜〜〜 (1-2) ・→ ●○ ＡＢ ＡとＢが衝突 〜〜〜〜〜〜 (1-3) ・→ ●○Ａが静止し，Ｂが遠ざかる様に動き始める． ＡＢ

図２３つの衝突

(2-1) →→・ ○○● ＡＢＣ 〜〜〜〜〜〜 (2-2) →・→

○●○ ＡＢＣＢとＣが衝突

〜〜〜〜〜〜 (2-3) ・→→ ●○○直ぐに，ＡとＢが衝突 ＡＢＣ 〜〜〜〜〜〜 (2-4) ・ →→ ● ○○ Ａ ＢＣ </pre>

こんな感じから，段々と複雑な現象を考えられませんか？

toorisugari no Hiro さんのレス (2009/09/05(Sat) 21:07)

> でも物理的，初歩的にはこの「静止」は必ずしも自明ではないようです．

わ，早速指摘された．そうなんですよね．

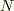個の粒子が固まってぶつかって 個の粒子がはじけるとき，

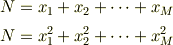
を満たさなければいけないのですが，

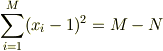
により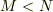， なら解はないことは言えても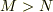， の否定はできないのです．

これはご指摘の通り，衝突の素過程を考えないとわかりませんね．

Yokkun さんのレス (2009/09/05(Sat) 21:09)

mNejiさん，かぶっちゃってごめんなさいm_ _m．

mNeji さんのレス (2009/09/06(Sun) 04:07)

もしこのおもちゃをお持ちでしたら，実際に衝突を起こす時の音をお聞きになれると思うのですが，衝突に際して「ジッ」というような音はでませんか？

と思ったのですが，「ニュートンのゆりかご」で検索すると別名「カチカチ」という説明はありましたが「ジッ」というような擬音は皆無なようです．流石，人間の耳には聞こえないくらいに短い時間現象なのでしょうね．

toorisugari no Hiro さんのレス (2009/09/06(Sun) 10:56)

> 今度は片側から２個，逆側から１個を同時にぶつけてみると，２個ぶつけた反対側で２個，１個ぶつけた反対側で１個はじけます．１個分のエネルギーが真ん中で打ち消しあって，１個だけがはじけたりしないのは何でなんでしょうか？

片側から1個，逆側から１個を同時にぶつけてみると，「真ん中で打ち消しあって，」何も動かない?

さらに，2個のコインを同じ速さで逆向きに直接衝突させたら「真ん中で打ち消しあって，」2個のコインがくっついて静止するのでしょうか?

そもそも「エネルギー」は打ち消されることはありません．熱や光や音，あるいは，コインの振動やコインの破壊の仕事などに形を変えることはあっても，消えることはありません．さらに，今回は「弾性衝突」ですから「運動」以外に形を変えられません．

ですから，2個の同じコインを同じ速さで逆向きに衝突させたらそれぞれの速度を交換する事しかできません．同様に「片側から２個，逆側から１個を同時にぶつけてみると，２個ぶつけた反対側で２個，１個ぶつけた反対側で１個はじけ」るしかできません．

イーさん さんのレス (2009/09/06(Sun) 23:36)

短い時間でたくさんの回答ありがとうございます．

一つ一つの衝突を個別に考えるのと，ぶつかっても打ち消しあわない，という理解を素人なりにしました．

複数個をテープでくっつけてぶつけるというのもどうなるのか面白そうなので，明日試してみます．

mNeji さんのレス (2009/09/07(Mon) 12:21)

衝突の映像を探していたら，「ゴルフのティーショットのスロー映像．」；

・www.bless4you.info/04_1.html#T27

がありました．この先頭に，「衝突時に，ボールが大きく変形してから飛び出るところ」が出ています．

金属ボール同士の場合でも，変形はもっと小さいでしょうが，本質的に似た事が起こっていると思います．ご参考まで．

イーさん さんのレス (2009/09/09(Wed) 00:37)

＞実は2個をテープで一体化して衝突させると，2個飛び出すという現象は起こらず，止まる球はひとつもなく，全部がばらばらになって前進する結果が得られます．

やってみました． ??をテープでくっつけて衝突させてみました．

通常なら??が一緒にはじけるはずですが，?が大きめに，?が中くらい，?が微妙に動きました．それらが帰ってきてぶつかると??がはじけるんですが，揺れの行ったり来たりが４〜５回で終わってしまいます．大きさが不ぞろいだと，力がうまく伝わり続かないようです．

mNeji さんのレス (2009/09/09(Wed) 02:02)

＞大きさが不ぞろいだと，力がうまく伝わり続かないようです．

細いステンレスの針金でタイトに縛るとどうでしょうか？

Yokkun さんのレス (2009/09/09(Wed) 08:44)

>通常なら??が一緒にはじけるはずですが，?が大きめに，?が中くらい，?が微妙に動きました．それらが帰ってきてぶつかると??がはじけるんですが，揺れの行ったり来たりが４〜５回で終わってしまいます．大きさが不ぞろいだと，力がうまく伝わり続かないようです．

これが理論通りの結果です．振り子の周期は振幅に依存し，またこの場合に静止する球はひとつもありませんから，もとには戻らず，ランダムに見える衝突を繰り返してエネルギーが全球に拡散します．もちろん，結合した2球の衝突が芯をとらえた正面衝突になりにくいということも影響はしているでしょう．しかし，質量2倍の球をぶつけてもはじめの方の運動は同じようになるはずです．

理論上は，衝突直前の2球の速度を として，衝突後の速度は

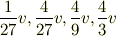
となり，十分離れたところで ○○○○○ というような並びになります．