花園 さんの書込 (2009/09/02(Wed) 20:58)

傾きθの斜面上に半径R，長さL，質量Mの中が空洞の円柱が，置かれている．この円柱は斜面を滑らずに転がる場合を考える． 重力加速度をg，円柱に作用する重力の大きさをMg，円柱が斜面から受ける摩擦力をF，垂直効力をNとする． このとき，円柱の重心の運動方程式を書け． なお，斜面に水平，垂直なx,y軸からなる座標軸を考え，円柱の重心の座標をX，Y，時間をtとする．

という問題があるのですが，座標軸を考えるということがよくわかりません．

普通に N=Mgcosθ F=Mgsinθ じゃだめなんでしょうか？？

yama さんのレス (2009/09/02(Wed) 22:03)

だめです． 花園さんが書かれた式は，斜面上に静止している物体の釣り合いの式であって運動方程式にはなっていません．

Yokkun さんのレス (2009/09/02(Wed) 22:42)

「垂直効力」は『垂直抗力』の誤変換として，「水平，垂直」は『平行，垂直』の誤りですね？

花園 さんのレス (2009/09/02(Wed) 22:49)

もしかしたら，わかったかもです．

m(d^2r/dt^2)=Fより

d^2X/dt^2=gsinθ d^2Y/dt^2=-gcosθ という感じでしょうか？？

それからその円柱に作用する力のモーメントの求め方は， 角運動量L=MR^2ωより， dL/dt=MR・d√{(d^2X/dt^2)^2+(d^2Y/dt^2)^2}/dt であってますでしょうか？？

垂直抗力ですね(笑) 問題も水平になっています・・・確かに平行の間違いだと思いますね．

Yokkun さんのレス (2009/09/02(Wed) 23:05)

運動方程式

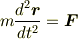
の右辺のＦは合力です． つりあいの式は，左辺の力を右辺にまとめれば加速度ゼロの運動方程式に他なりませんから，よーく考えて． x軸，y軸はどちら向きにとりますか？力の矢印はちゃんと描けていますか？

花園 さんのレス (2009/09/02(Wed) 23:48)

あ，そうですよね・・・

>>つりあいの式は，左辺の力を右辺にまとめれば加速度ゼロの運動方程式に他なり >>ませんから，よーく考えて． 力の向きを考えろってことですかね？？

X軸方向の力，Y軸方向の力それぞれ足すと

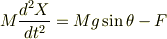
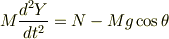
こんな感じでしょうか？？

Yokkun さんのレス (2009/09/03(Thu) 08:28)

x軸を斜面降下方向，y軸を斜面垂直上方にとられたのですね． 運動は斜面に拘束されていて加速度y成分はゼロになることはいうまでもありません．

>円柱に作用する力のモーメントの求め方は， 角運動量L=MR^2ωより， dL/dt=MR・d√{(d^2X/dt^2)^2+(d^2Y/dt^2)^2}/dt ・・・

力のモーメントは運動方程式右辺です． 左辺の角運動量は，すべらずに転がる条件から

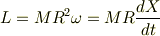
ですよね？速度が加速度になっちゃってます．

花園 さんのレス (2009/09/03(Thu) 12:19)

あ，確かにy軸方向には円柱は動きませんよね・・・ だから，NとMgcosθはつりあってて， d^2Y/dt^2=0 になるんですね．

そして，dY/dt=0なので， 角運動量L=MR・dX/dt 力のモーメントは dL/dt=MR・d^2X/dt^2 となるんでしょうか？？

mNeji さんのレス (2009/09/03(Thu) 14:34)

花園さん，横から失礼します．

問題には「FとNとの関係」は記述されていないのでしょうか？

また円柱の厚さには説明はないのでしょうか？円柱の角運動量はどこの軸廻りに付いて考えているか判っていますか？

式の書き方ですが；

begin{eqnarray} Mfrac{d^2X}{dt^2}=Mgsinθ-F end{eqnarray}

この数学掲示版では， begin{eqnarray}→<ｔｅｘ> end{eqnarray}→<／ｔｅｘ> ただし，半角にしてください．

すると，

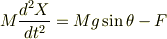
このテキストを書き出すと； <ｔｅｘ> Mfrac{d^2 X}{d t^2}=Mgsintheta-F <／ｔｅｘ>

このように，数式中には半角の英数しか使えません．また初等関数には「」を付ければ「立体」にしてくれるので，変数との見分けが明瞭になります．

もし，文中に入れたければ，<ｔｅｘ>や<／ｔｅｘ>と数式の間に「リターンをなくす」と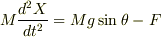， となります．