ローレンツ変換について
ローレンツ変換について
Gen(大学2年) さんの書込 (2009/08/31(Mon) 11:31)
このごろ私は特殊相対性理論を学んでいます.その過程のローレンツ変換について疑問を感じる事態に陥りました.そこで,そのことについて教授していただきたく投稿させたもらいました.なにぶん,まだ,特殊相対性理論が不十分のため,変ないいましをして,文章が意味が分からなくなることが懸念されますが,そこのところは読み解いてもらえれば,幸いです. ローレンツ変換を導くまでの過程でx=A(x'-vt)が示される(Aは定数とする).なぜ,Aをかけても式が成り立っているのか.という疑問が残る.要するに,x=x'-vtは,図などから数式的(数学的)に成立していたが,x'-vtにAを掛けると数式的(数学的)に成立しなくなる.念のため,別の例で述べると,1=1で成立するものが,1=1×2で成立するといっているような感じがある.どうしてなのだろうか?.まぁ,こんな感じです.どうかこの解説をしていただけないでしょうか.お願いします.
Re: ローレンツ変換について
ミュフ猫 さんのレス (2009/08/31(Mon) 11:50)
2直線:ct=±x 上のあらゆる点が不動点になる一次変換を考えればいいかも.
Re: ローレンツ変換について
Gen(大学2年) さんのレス (2009/08/31(Mon) 14:46)
ミュフ猫さん回答ありがとうございます. すいませんが,馬鹿な私には良くわからないのです.どのように ミュフ猫さんの見解がこの問題に対してリンクし,解法につながるか.よくわかりません.すいませんが,もう少し,やわらかく説明をしていただけたらうれしいのですが.お願いします.
Re: ローレンツ変換について
ミュフ猫 さんのレス (2009/08/31(Mon) 16:01)
うわ〜!ぜんぜん駄目ですね.条件キツ過ぎ.不動直線になるってだけでいいのかな?
すいません.間違いました.忘れてください.m(_ _)m
Re: ローレンツ変換について
toorisugari no Hiro さんのレス (2009/08/31(Mon) 17:16)
> ローレンツ変換を導くまでの過程でx=A(x'-vt)が示される(Aは定数とする).
?
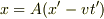 の間違いではないですか?
の間違いではないですか?
X系の原点 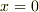 は(X系に対して速度
は(X系に対して速度 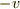 で動く)X'系(ただし,
で動く)X'系(ただし, 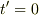 でX系とX'系の原点は一致する)からみると
でX系とX'系の原点は一致する)からみると 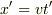 を満たす直線上にあるという条件
と
ローレンツ変換の線形性の仮定
を満たす直線上にあるという条件
と
ローレンツ変換の線形性の仮定 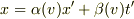 から
から
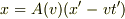 とおける訳ですよね.
とおける訳ですよね.
> 別の例で述べると,1=1で成立するものが,1=1×2で成立するといっているような感じがある.
というより,0=0×1で成立するものが,0=0×Aとなっただけですよね. ニュートン力学ではA=1ですが,A=1と決めうちしなかったらどんな式ができるかという話だと思います.
Re: ローレンツ変換について
Yokkun さんのレス (2009/08/31(Mon) 21:28)
私もけっこう悩みました.未だにすとんと落ちる感じはしませんが. 大方のテキストでは,さらーっと流している部分ですよね. toorisugari no Hiroさんの「ローレンツ変換の線形性の仮定」という説明である程度納得がいきます.
ちなみに,Relativity (A.Einstein 1916)
のAppendix A P.93〜によると,もう少しトリッキー(?)な解説をしていて興味深いです.
要約すると, 慣性系であるK系で,t=0に原点からx方向に発せられた光において,
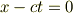
t=t'=0でK系と原点が一致するもうひとつの慣性系であるK'系で
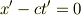
が成立しなければならない(光速不変).すると,一般の事象点において
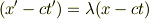
が成立すべきである.x軸負の方向への光に対する考察から同様に
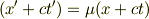
ここで,
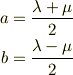
と置くと,K系からK'系への変換が上の2式より
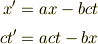
と導かれる.ここで,K'系の原点x'=0の運動について考えると
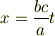
となるから,
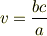
に他ならない.
…といった具合.
Re: ローレンツ変換について
Gen(大学2年) さんのレス (2009/08/31(Mon) 21:59)
toorisugari no Hiroさん,回答ありがとうございました. toorisugari no Hiroさんの言うとおり,x=A(x'-vt)はx=A(x'-vt')の間違いです. お手を掛けますがtoorisugari no Hiroさんの教えをわたしなりに理解しましたが,その理解は正しいのか.判断できませんので合っているか.確認をしてほしと思います.よろしくお願いします.(ローレンツ変換の線形性の仮定をこのように考えて間違いないか.)S系とS'系の任意の点Pは固定されていて,相対速度vによって,vt’とx’の比率を変える.よって,x=α(v)x'-β(v)vt'で示せる.
Re: ローレンツ変換について
Gen(大学2年) さんのレス (2009/08/31(Mon) 22:38)
Yokkunさん,回答ありがとうございました. 英語がまったく読めないので,要約していただき助かります. 本当に興味深い導き方をしていますね.でも,かなり高度で,理解ができませんね.ある一点だけ質問しますが,(λ倍するところなんですが・・・)x-ctとx'-ct'のでる出る解は違うものがでることが懸念されることからλをかけて,帳尻合わせをしているんですかねぇ.
Re: ローレンツ変換について
toorisugari no Hiro さんのレス (2009/09/01(Tue) 09:17)
> (ローレンツ変換の線形性の仮定をこのように考えて間違いないか.)S系とS'系の任意の点Pは固定されていて,相対速度vによって,vt’とx’の比率を変える.よって,x=α(v)x'-β(v)vt'で示せる.
たぶん,違うと思います.
ローレンツ変換の線形性の仮定の出発点は「時空の一様性(affine性)」(=時空の原点の取り方に物理法則は依存しない)です.これは,ガリレイ変換でも成り立ちます.
慣性系Xがあり,X系に対して一定一様な速度  で動く慣性系X'があるとし,適当に決めた原点のもと,X系とX'系の間に
で動く慣性系X'があるとし,適当に決めた原点のもと,X系とX'系の間に
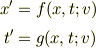
という関係が成り立つとします.
いま, 原点を 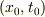 に取り直すとします.
時空の一様性により,新しい原点のもとでも上の法則は成り立つとすると,
に取り直すとします.
時空の一様性により,新しい原点のもとでも上の法則は成り立つとすると,
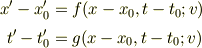
が成り立ちます.ただし,
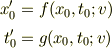
です.
これより,
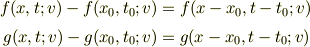
が恒等的に成り立ちます.
一般に,
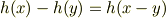
が任意の 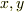 で成り立つなら
で成り立つなら 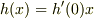 となるので,
となるので,
同様に 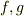 も
も
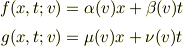
という形になります.
参考: 「相対論的物理学のききどころ」和田純夫 岩波書店
Re: ローレンツ変換について
Yokkun さんのレス (2009/09/01(Tue) 14:05)
Genさん,アインシュタインの展開は基本的にtoorisugari no Hiroさんの説明にあるように
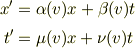
とおくことと違いがあるわけではありません.変換の線形性を仮定した上で,両慣性系で光の世界線

が一致すること(光速不変)を先に考慮して未知の係数の数をあらかじめ減らしただけです.ですから,

( 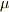 がかぶっちゃいましたが)
という限定(係数が相対速さのみで決まること)もtoorisugari no Hiroさんの
がかぶっちゃいましたが)
という限定(係数が相対速さのみで決まること)もtoorisugari no Hiroさんの

と同等であることは,結果的に
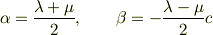
となることからも明らかです.
アインシュタインの展開は,はじめに
 の関係を前提したということになります.
の関係を前提したということになります.
Re: ローレンツ変換について
Gen(大学2年) さんのレス (2009/09/01(Tue) 14:43)
toorisugari no Hiroさん,Yokkunさん,双方の方々には再度の質問にご回答いただきありがとうございました.toorisugari no Hiroさん,分かりやすい説明ありがとうございます.完全とまではいかないものの,おおまかに理解ができた感じがあります.参考の本まで挙げてもらい,助かります.早速買って呼んでみたいと思います.Yokkunさんの説明で特に:>(光速不変)を先に考慮して未知の係数の数をあらかじめ減らしただけです.の所はわかりやすく納得できました.双方の方々詳細な説明をしていただき,ありがとうございました.