中心力場とは？

home > 掲示板 >

このページのPDF版

サイトマップ

中心力場とは？

高校時代生物選択さんの書込 (2009/08/30(Sun) 13:38)

またもや質問させて頂きます．・・・申し訳ないです．

授業で中心力場という言葉がポンと出て来てしまったのですが，なんのことだか一向にイメージがわきません．

そもそも，中心力という言葉の概念自体が曖昧で，自分でも調べてみてもよくわかりません．

授業では

中心力場は

Fｒ＝−ｄU（ｒ）/ｄｒ Fθ＝０

という極座標表示で表現される，というように解説されたのですが・・・．

Re: 中心力場とは？

mNeji さんのレス (2009/08/30(Sun) 19:26)

一つ戻って，中心力とは，原点からの位置ヴェクタに比例した力を意味します．例えば，重力とかクーロン力(静電荷間の力)がそうです．糸の先に錘をつけて回転させた時の糸の張力も中心力です．

で，重力とかクーロン力とかのように，位置ヴェクタの距離だけに依存する力の場合は，ポテンシャルから導く事ができます．そのような場合，中心力の場，中心力場と呼ぶのだろうと思います．

「糸の先の錘」の場合，中心力ではありますが，回転速度の与え方によっても力の大きさが変わってしまう為にポテンシャルを与える事ができません．従って，この場合には，中心力であるが，中心力場とは呼べないと思います．

Re: 中心力場とは？

高校時代生物選択さんのレス (2009/09/01(Tue) 23:42)

遅くなり申し訳ありません．

位置ベクトルに「のみ」比例する力ということでしょうか？

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 00:06)

＞位置ベクトルに「のみ」比例する力ということでしょうか？

丁寧に書けば，

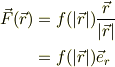
$\vec F(\vec r) &= f(|\vec r|)\frac{\vec r}{|\vec r|}\\&= f(|\vec r|)\vec e_r$

といったところでしょうか．

逆に「質量mの質点」に，上記の力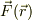， $\vec F(\vec r)$ が加わって，地点 $\vec r_0$ から $\vec r$ まで動いた時に，其の力が質点にする仕事はどうなるでしょうか？

Re: 中心力場とは？

toorisugari no Hiro さんのレス (2009/09/02(Wed) 10:44)

横から失礼します．中心力の定義というのもよく考えると難しいですね．

普通は角運動量保存則が常に成り立つような力として，定義されます．つまり，

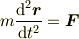
$m\frac{\mathrm{d}^2 \bm{r}}{\mathrm{d}t^2} &= \bm{F}$

の両辺に $\bm{r}$ を外積でかけて

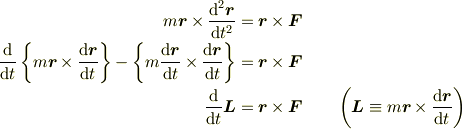
$m\bm{r} \times \frac{\mathrm{d}^2 \bm{r}}{\mathrm{d}t^2} &= \bm{r} \times \bm{F}\\\frac{\mathrm{d}}{\mathrm{d}t} \left\{ m\bm{r} \times \frac{\mathrm{d} \bm{r}}{\mathrm{d}t}\right\} -\left\{ m\frac{\mathrm{d} \bm{r}}{\mathrm{d}t} \times \frac{\mathrm{d} \bm{r}}{\mathrm{d}t}\right\} &= \bm{r} \times \bm{F}\\\frac{\mathrm{d}}{\mathrm{d}t}\bm{L} &= \bm{r} \times \bm{F}\qquad\left(\bm{L} \equiv m\bm{r} \times \frac{\mathrm{d} \bm{r}}{\mathrm{d}t}\right)$

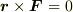より， $\bm{r} \times \bm{F}=0$ であれば，すなわち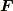， $\bm{F}$ が $\bm{r}$ に平行

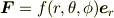
$\bm{F} = f(r,\theta,\phi) \bm{e}_r$

であれば角運動量 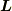$\bm{L}$ が保存するので，上のような形式の力を中心力といいます．ここで，はのみの関数でなくてもかまいません．

ただし，力が保存力だとしたら

$\bm{F} = -\mathrm{grad\,}U(\bm{r}) \qquad (\Leftrightarrow \mathrm{rot\,}\bm{F} = 0)$

でなければいけません．つまり，

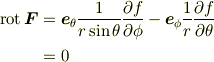
$\mathrm{rot\,}\bm{F} &= \bm{e}_\theta \frac{1}{r\sin\theta}\frac{\partial f}{\partial \phi}- \bm{e}_\phi \frac{1}{r}\frac{\partial f}{\partial \theta}\\&=0$

であるので，はのみの関数となり，

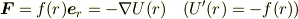
$\bm{F} &= f(r) \bm{e}_r = - \nabla U(r) \quad (U'(r) = -f(r))$

が成立します．

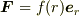# $\bm{F} = f(r) \bm{e}_r$ を「中心力」と呼ぶ文献もあれば，「保存的な中心力」と区別して呼ぶ文献もあり，定まっていない印象があります．

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 14:49)

多少異論があるのでコメントさせて戴きます．

＞普通は角運動量保存則が常に成り立つような力として，定義されます．

この「普通」というのはどのくらい普通なものなんでしょうか？私の記憶では，地球の太陽に対する運動をニュートンの運動方程式を使って解く時に，動径方向と，接線方向に分けて書き出した時に，接線方向の力の成分がゼロだから，「面積速度=0」と置けると出てきたと思います．

勿論，お説のように角運動量の時間微分の論議を持ち込むのに異論はありませんが，運動方程式自身にその情報が既に入っている事を認識することを忘れてはいけないと思います．

また角運動量は，素直に

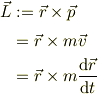
$\vec L &:= \vec r \times \vec p\\&= \vec r \times m\vec v\\&= \vec r \times m\frac{\mathrm{d}\vec r}{\mathrm{d}t}$

とするほうが誤解されにくいと思います．

＞はのみの関数でなくてもかまいません．

論理的にはそうだと思いますが，どのような事例がありますか？

Re: 中心力場とは？

toorisugari no Hiro さんのレス (2009/09/02(Wed) 15:00)

> 「面積速度=0」と置けると出てきたと思います．

「面積速度一定」ではなくてですか?

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 15:54)

＞「面積速度一定」ではなくてですか?

間違えました．「面積速度の微分=0」と修正しておきました．他の文も，あまり判りよくないですが，後ほど訂正します．取り急ぎ，失礼します．

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 18:31)

面積速度の件で，補足説明をします．

遠い昔の事なのですが，運動方程式を実際に応用するのが嬉しかったころ，惑星の運動を解くのに必至だった頃，「面積速度の時間変化＝０」がなかなか納得出来なかったような気がします．

丁度，そのころ；

・運動方程式；言い換えれば「運動量の時間変化＝全ての外力の和」・角運動量の式；言い換えれば「角運動量の時間変化＝全ての外力によるトルクの和」

を知って感激した記憶があります．そこで，逆に「面積速度の時間変化＝０」が納得出来たように思います．でも，重要なのは，「面積速度の時間変化＝０」は運動方程式の接線方向の成分がゼロという事から直接的に得るものであります．

運動方程式を解くにあたって，別途，角運動量の式を独立に解かないといけないという事を要請していない，と言うことを指摘したかったものです．

他方，剛体系では，運動方程式と角運動量の式とを同時に考える必要がありますね．

Re: 中心力場とは？

toorisugari no Hiro さんのレス (2009/09/02(Wed) 19:02)

> でも，重要なのは，「面積速度の時間変化＝０」は運動方程式の接線方向の成分がゼロという事から直接的に得るものであります．

良く意味がつかめませんが，これは力の軌道接線成分あるいは加速度の軌道接線成分がゼロという意味のことをおっしゃっているのでしょうか? それからは「速さの時間変化＝０」は導けても，「面積速度の時間変化＝０」であることは導けませんが．

面積速度は定義により 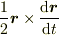$\frac{1}{2}\bm{r}\times\frac{\mathrm{d}\bm{r}}{\mathrm{d}t}$ ですが，「面積速度の時間変化＝０」は

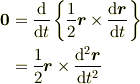
$\bm{0} &= \frac{\mathrm{d}}{\mathrm{d}t}\left\{\frac{1}{2}\bm{r}\times\frac{\mathrm{d}\bm{r}}{\mathrm{d}t}\right\}\\&= \frac{1}{2}\bm{r}\times\frac{\mathrm{d}^2\bm{r}}{\mathrm{d}t^2}$

であり，「加速度が動径に平行」が導けるのであって，円軌道でもない限り加速度の軌道接線成分はゼロにはなりませんよね．

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 21:01)

今，簡単の為に平面上にある質点に中心力が働いている場合を考えます．

運動方程式は；

$m\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2} &= f(r)\vec e_r &\ ---(1)$

となります．極座標表示で考えると；

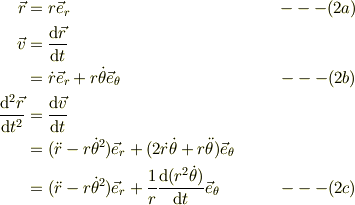
$\vec r &= r\vec e_r &\ ---(2a)\\\vec v &= \frac{\mathrm{d} \vec r}{\mathrm{d} t}\\&= \dot r \vec e_r + r \dot \theta \vec e_{\theta} &\ ---(2b)\\\frac{\mathrm{d}^2 \vec r}{\mathrm{d} t^2} &= \frac{\mathrm{d} \vec v}{\mathrm{d} t}\\&= (\ddot r -r\dot \theta^2) \vec e_r +(2\dot r \dot \theta +r\ddot \theta)\vec e_{\theta}\\&= (\ddot r -r\dot \theta^2) \vec e_r +\frac{1}{r}\frac{\mathrm{d}(r^2\dot \theta)}{\mathrm{d} t}\vec e_{\theta} &\ ---(2c)$

となりますから，式(1)の左辺に式(2c)を適用すれば，成分毎に

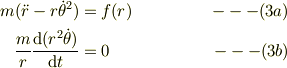
$m(\ddot r -r\dot \theta^2) &= f(r) &\ ---(3a)\\\frac{m}{r}\frac{\mathrm{d}(r^2\dot \theta)}{\mathrm{d} t}&=0 &\ ---(3b)$

となるように思います．

ちなみに角運動量；

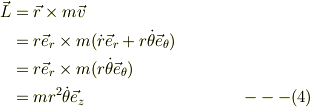
$\vec L &= \vec r \times m \vec v\\&= r \vec e_r \times m (\dot r \vec e_r + r \dot \theta \vec e_{\theta})\\&= r \vec e_r \times m (r \dot \theta \vec e_{\theta})\\&= mr^2 \dot \theta \vec e_z &\ ---(4)$

式(3b)より直接的に，「式(4)が時間的に一定のヴェクタである」ことを導き出せます．

Re: 中心力場とは？

toorisugari no Hiro さんのレス (2009/09/02(Wed) 21:10)

> となるように思います．

この計算は座標変換しかしてないので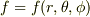， $f=f(r,\theta,\phi)$ の場合でも，

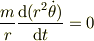
$\frac{m}{r}\frac{\mathrm{d}(r^2\dot \theta)}{\mathrm{d}t} = 0$

が成り立ちますよね．

Re: 中心力場とは？

mNeji さんのレス (2009/09/02(Wed) 21:46)

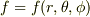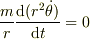＞この計算は座標変換しかしてないので， $f=f(r,\theta,\phi)$ の場合でも，＞ $\frac{m}{r}\frac{\mathrm{d}(r^2\dot \theta)}{\mathrm{d}t} = 0$ ＞が成り立ちますよね．

勿論そう思います．

でも，実際に，その様に複雑な力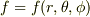， $f=f(r,\theta,\phi)$ を知りません．むしろ余程の事が無い限り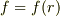， f=f(r) と単純にイメージして，動径方向の微分方程式をどうのように解釈したり，解いたりしたりして，次のステップに進める方が大切な様に感じます．

特に，ご質問者の方は，高校時代に物理を選択されなかったと仰っている訳ですし，設問自体もポテンシャルを導こうとしていると推測されます．そのような段階に，複雑な条件とか，ヴェクタ解析からの説明(力の回転)をいれると，混乱し易いのではないでしょうか．

Re: 中心力場とは？

anon さんのレス (2009/09/03(Thu) 16:41)

ちょっと話の内容が元質問者さんには難しくなってきて，反応できなくなっているのではないでしょうか？

「中心力場」というのは，「中心力」からなる「力の場」のことで，「中心力」というのは，空間のどこに於いても中心のある一点へ向かう力（あるいは中心と反対の方向へ向かう力）が働いているような状況を表します．

ですから，極座標で表現すると次のようになります．

空間のある場所に於いて働く力を，中心方向（動径方向）成分と偏角方向（動径に垂直な方向）成分に分けたとき，中心方向成分（Fｒ）はともかくとしても，偏角方向成分（Fθ）は0となるわけです．

中心方向成分については，（特に中心力場でなくとも<ins>保存力でありさえすれば</ins>一般的に成立するとおり，）力がポテンシャルの微分として表せることになります．（Fｒ＝−ｄU（ｒ）/ｄｒ）

ところで， mNejiさんの仰る， > 中心力とは，原点からの位置ヴェクタに比例した力を意味します．というのは少し特殊な状況で，一般的には，力が位置ベクトルと平行であるというだけです． ## あるベクトルが他のベクトルと平行である，ということは， ## あるベクトルが他のベクトルのスカラー倍になる，ということでもあるわけですが，これを， ## あるベクトルが他のベクトルに比例する，と表現してしまうと誤解を招くと思います． ## 「比例」というのは，上の「スカラー倍」のスカラーが， ## どこでも一定の「比例定数」になっている状況を表しますよね．

（一部追記しました．「保存力でありさえすれば」を挿入．）

Re: 中心力場とは？

mNeji さんのレス (2009/09/03(Thu) 18:49)

anonさん，

＞mNejiさんの仰る，＞> 中心力とは，原点からの位置ヴェクタに比例した力を意味します．＞というのは少し特殊な状況で，一般的には，＞力が位置ベクトルと平行であるというだけです．

確かに言葉での説明とすると誤解を受け易いのかも知れませんが，その後に付け加えた；

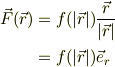
$\vec F(\vec r) &= f(|\vec r|)\frac{\vec r}{|\vec r|}\\ &= f(|\vec r|)\vec e_r$

はどうなのでしょうか？それとも，絶対値を抜いた，

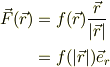
$\vec F(\vec r) &= f(\vec r)\frac{\vec r}{|\vec r|}\\ &= f(|\vec r|)\vec e_r$

これなら納得出来るのでしょうか？

何れにしろ，私のイメージでは，

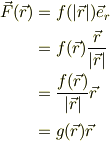
$\vec F(\vec r) &= f(|\vec r|)\vec e_r\\&= f(\vec r)\frac{\vec r}{|\vec r|}\\&= \frac{f(\vec r)}{|\vec r|}\vec r\\&= g(\vec r)\vec r$

と言う点を強く感じている様です．

Re: 中心力場とは？

anon さんのレス (2009/09/03(Thu) 19:42)

mNejiさんへ

えっと，その続きの部分も読んでいただきたかったのですが，要は， No.25461の最後に出てくる g(r) が r によらない定数になる場合でないと「比例する」とはいわないのではないか，ということなのです．

Re: 中心力場とは？

mNeji さんのレス (2009/09/03(Thu) 20:38)

anonさん，

＞No.25461の最後に出てくる g(r) が r によらない定数になる場合でないと＞「比例する」とはいわないのではないか，ということなのです．

そうですか，数学的に厳密に説明するのは難しいですね．

少なくとも，自分の言葉による説明は撤回して，式に依る説明に統一します．ご教示感謝します．

Re: 中心力場とは？

mNeji さんのレス (2009/09/04(Fri) 04:22)

中心力を言葉によって説明する事を再度考えて見ました．

中心力とは，考える位置での位置ヴェクタの方向を向き，其の強さは位置の関数である力である．

中心力に対しては，角運動量が保存される．

また中心力の強さが，位置ヴェクタの絶対値にのみ依存する場合，別々の２点を結ぶ線積分は，其の経路によらない．この場合，この力は保存力と言われ，その線積分はポテンシャルと関連する．

Re: 中心力場とは？

ミュフ猫さんのレス (2009/09/04(Fri) 07:57)

それだと，位置ベクトルの基準点以外の一点に集結するような力場は中心力場と言えなくなるのでは？単に，「力線が放射線状の力場」では駄目ですかね．

Re: 中心力場とは？

mNeji さんのレス (2009/09/04(Fri) 11:02)

＞それだと，位置ベクトルの基準点以外の一点に集結するような力場は中心力場と＞言えなくなるのでは？

そうですね，この点を含めるには；

・相互作用が２体力で，・重心運動，相対運動に分けられて，・相互運動にだけ，２体力が顔をだす

といった流れを説明する必要がありますね．

＃私見では，力学を学び初めの段階では，この点には重点を置かなくても良いと考えます．＃せいぜい運動を考える質点の質量mが，他方の質点の質量Mに比べて十分に小さければ云々...，と言う様な説明で十分では？＃それでも納得しない場合に，「運動学」という分野があるので，調べる様に助言をすればいいかと思います．

＞単に，「力線が放射線状の力場」では駄目ですかね．

難しくしないで説明出来ますか？

Re: 中心力場とは？

ミュフ猫さんのレス (2009/09/06(Sun) 00:11)

>難しくしないで説明出来ますか？

いろいろ考えましたが，私には無理でした．

Re: 中心力場とは？

mNeji さんのレス (2009/09/06(Sun) 04:13)

＞いろいろ考えましたが，私には無理でした．

では，条件を緩和させてみたらどうでしょうか？色々な考え方に接する好例だと思います．

[home] [掲示板] [ページの先頭]