やす さんの書込 (2009/08/26(Wed) 08:50)

はじめまして．質問があります． 空気抵抗ありの落下運動に関する問題で，ある本では地面から上向きにｙ軸をとり，質量mの物体に下向きに重力-mg，上向きに空気抵抗-Bv(Bは正の定数)の力が働くとして，運動方程式が， ma=-Bv-mg となっていましたが， ma=-mg-(-Bv) =-mg+Bv ではなぜ駄目なのでしょうか？ 初心者なものでよろしくお願いします．

mNeji さんのレス (2009/08/26(Wed) 10:38)

すこし下に(一覧表示で19行ほど)，「落下の運動方程式」というタイトルで同様の論議がありますね．ご参考まで．

toorisugari no Hiro さんのレス (2009/08/26(Wed) 10:46)

> 上向きに空気抵抗-Bv(Bは正の定数)の力が働くとして，

問題文の表現が不適切ですね．「空気抵抗」は速さを減らす方向に働くので，速度が正なら「空気抵抗」は負の方向(速さは減少)，速度が負なら「空気抵抗」は正の方向(速さは減少)に働きます．つまり， 『 「空気抵抗」は「速度」に対して「逆向き」に作用する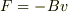． 』 と表現するのが適切であって，座標軸に対して向きを決めるものではありません．

問題文の場合「落下」なので速度は鉛直下向き方向つまりy軸の負の方向を向きます( 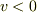)．ですから，空気抵抗は鉛直上向き(=正)で大きさは 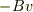，つまり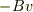， となるわけです．

# もちろん，物体が上昇中でも「空気抵抗」は 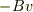です．ただし，力は下向きに働いてますよね．

やす さんのレス (2009/08/26(Wed) 12:03)

ありがとうございます． 参考にさせていただきます．

やす さんのレス (2009/08/26(Wed) 12:15)

わかりやすい解説ありがとうございます． ところで運動方程式の力Fは合力と考えればよろしいのでしょうか？ つまり先程の問題より， ma=（-Bv）＋（-mg）・・・? と考えればよろしいのでしょうか？ 自分の場合，Fは力の差と思っていましたので， -mg＞-Bvから， ma=（-mg）−(-Bv)・・・? ?式のようになると思っていました．

toorisugari no Hiro さんのレス (2009/08/26(Wed) 14:25)

> ところで運動方程式の力Fは合力と考えればよろしいのでしょうか？

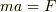の は質量 の質点に作用するすべての力の合力です．

ただし，ぞれぞれの力は向き(＝符号)を持っていますので，合力の大きさはそれぞれの力の大きさの「和」になるとは限りません．

anon さんのレス (2009/08/26(Wed) 14:32)

やすさんへ，ちょいと横から念押しですが， v自体が負の値なのですよ． 「符号つきの力」と「力の大きさ」は違う概念です．

# （追記） # あと，符号つきの重力の値は -mg ですが，重力の大きさは mg です．

やす さんのレス (2009/08/26(Wed) 15:51)

> ma=FのFは質量の質点に作用するすべての力の合力です．

なるほどそうなんですか． 基礎がわかっていませんでしたね・・・． 勉強し直します．

ありがとうございました！