電磁誘導
電磁誘導
花鳥風月 さんの書込 (2009/08/21(Fri) 08:49)
直線電流と距離rに平行におかれた,ループコイル内の磁束を求める問題です. コイルが四角形なら,B=μI/2πrdrの積分とかで出来るのですが, コイルが正三角形の場合はどのような計算で磁束を求められるのでしょうか? 図上手く書けなくて,わかりにくいと思いますが,ご教授お願いします.
――――――――――――――――――――→I
―――――――― / / / /
Re: 電磁誘導
toorisugari no Hiro さんのレス (2009/08/21(Fri) 12:32)
> コイルが四角形なら,B=μI/2πrdrの積分とかで出来るのですが, > コイルが正三角形の場合はどのような計算で磁束を求められるのでしょうか?
二重積分の片割れの区間が変化するだけで,あとは,同じようにやればいいはず.何も難しくないですよ.
Re: 電磁誘導
mNeji さんのレス (2009/08/21(Fri) 12:36)
長方形の場合が計算出来るのならば,正三角形を変形して,長方形の半分と見なす事が出来ますね.
<pre>
ABAB ・ーーーーーーーーー・・ーーーーーーーーー・ /| / /=|/ /| / /|/ ・・ CC’
AB ・ーーーーーーーーー・ 1|| =ー|| 2|| || ・ーーーーーーーーー・ C’D’ </pre>
Re: 電磁誘導
toorisugari no Hiro さんのレス (2009/08/21(Fri) 12:43)
mNejiさん 面積ではなく磁束の計算だから単純に半分にならないのでは? 直角三角形にするアイディアは採用!
Re: 電磁誘導
花鳥風月 さんのレス (2009/08/21(Fri) 12:50)
回答して頂いた方々に感謝いたします.
>>二重積分の片割れの区間が変化するだけで,あとは,同じようにやればいいはず.
二重積分はあまり理解できていなくて,,,.
>>長方形の場合が計算出来るのならば,正三角形を変形して,長方形の半分と見なす事が出来ますね.
底辺が同じだから,面積は等しいんですね.思いつきませんでした. ただ,1/2とありますが,二等分の仕方によって,磁束全体の和に影響しないでしょうか?B=μI/2πrdrという式から,距離rによって大きさが変わってきますよね? 直感的には,出来そうなのですが,もう1つ直感的に上記のことも考えてしまいました.
Re: 電磁誘導
mNeji さんのレス (2009/08/21(Fri) 12:51)
>面積ではなく磁束の計算だから単純に半分にならないのでは?
図を丁寧に書けないのですが,横方向に細長い短冊に切ったと考えれば(高さdr)とすれば,正三角形でも,直角三角形でも同じです.単にそれを2倍して長方形なので,厳密に成り立つと思いますが....
<pre> ー+ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー→ I | | |■■■■■■■■■■■■■■■■■■■■■■■■■■↓dr | ■■■■■■■■■■■■■■■■■■■■■■ |■■■■■■■■■■■■■■■■■■ | ■■■■■■■■■■■■■■ |■■■■■■■■■■ |■■■■■■ ↓■■ r
</pre>
Re: 電磁誘導
mNeji さんのレス (2009/08/21(Fri) 13:25)
済みません.間違っていますね.きちんと積分は実行しないと駄目ですね.
その計算の時に,直角三角形としておけば,ちょっとご利益があるというだけです.ご免なさい.
Re: 電磁誘導
toorisugari no Hiro さんのレス (2009/08/21(Fri) 13:41)
> 二重積分はあまり理解できていなくて,,,.
軸を  軸をとり,正三角形の重心の
軸をとり,正三角形の重心の  座標を0とします.軸からの距離を
座標を0とします.軸からの距離を  として,点
として,点 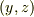 を正三角形を含む平面の座標とします.
を正三角形を含む平面の座標とします.
(1)点 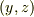 が一辺が
が一辺が  の正三角形に含まれる条件は?
(2)点
の正三角形に含まれる条件は?
(2)点 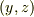 を重心とする
を重心とする 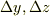 の微小な長方形を考えます.この長方形の磁束を近似計算してください.
(3)(1)の条件を満たすすべての
の微小な長方形を考えます.この長方形の磁束を近似計算してください.
(3)(1)の条件を満たすすべての 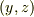 について(2)を足し合わせます.
(4)形式的に二重積分ですが,簡単に1重積分になります.あとは積分する.
について(2)を足し合わせます.
(4)形式的に二重積分ですが,簡単に1重積分になります.あとは積分する.
結果は余りきれいな式にはならないが,計算は難しくない.
Re: 電磁誘導
花鳥風月 さんのレス (2009/08/22(Sat) 12:54)
ありがとうございます.
z軸は,横軸にして,縦軸にy軸をとるということですか? そして,原点に重心をもってくるという図でしょうか? 二次元の積分が,一次元の積分になることが,想像できないのですが.
ちなみに,二重積分以外で,他の方法とかはありますか?
Re: 電磁誘導
yama さんのレス (2009/08/22(Sat) 15:10)
正三角形を電流に平行な長辺を持つ多数の細長い長方形に分割して考えてみましょう.
その長方形の長辺の長さを 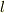 ,短辺の長さを
,短辺の長さを 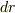 とすると,その面積は
とすると,その面積は 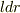 になるので,磁束は
になるので,磁束は 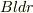 です.
正三角形全体の磁束はこれを積分したものです.
です.
正三角形全体の磁束はこれを積分したものです.
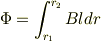
ここで 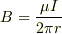 です.
また
です.
また 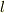 は
は  の関数であり,
の関数であり, 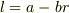 のように一次式で表されることが分かります.
従ってこの積分は簡単に計算できます.
もちろん
のように一次式で表されることが分かります.
従ってこの積分は簡単に計算できます.
もちろん 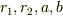 については,問題で与えられた値を用いて表さないといけません.
しかしその値を代入するのは最後の段階でいいでしょう.
については,問題で与えられた値を用いて表さないといけません.
しかしその値を代入するのは最後の段階でいいでしょう.
ところで,磁束を二重積分で表せば
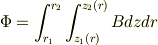
となりますが, 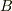 が
が  だけの関数なので,
だけの関数なので,  についての積分は単に積分区間の幅
についての積分は単に積分区間の幅 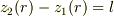 を掛けるだけになり,結局は上記の積分に帰着されるわけです.
を掛けるだけになり,結局は上記の積分に帰着されるわけです.
なおtoorisugari no Hiro さんとは,原点のとりかたなどが違いますが,積分の結果は同じになるはずです.
Re: 電磁誘導
花鳥風月 さんのレス (2009/08/22(Sat) 19:40)
少しわかってきた気がします.有難うございます. しかし. l=a-br という式が理解できないです. rとlは,同じ方向の成分ではないですよね? それと,z軸の位置関係がまだわかっていません. 最初の図においては,どの方向でしょうか?
Re: 電磁誘導
yama さんのレス (2009/08/22(Sat) 20:30)
直線電流をz軸にとります.
rはz軸からの距離です.
電流に平行で電流からの距離がrである直線を考えると,その直線と三角形との交点が2つあります.(rの値によっては交点がない場合もあります.)
その2点間の距離が 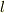 です.
従って
です.
従って 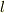 はrと垂直な方向(すなわちz方向)に測ります.
はrと垂直な方向(すなわちz方向)に測ります.
Re: 電磁誘導
花鳥風月 さんのレス (2009/08/23(Sun) 00:19)
状況は把握できました.
一応,問題は,
無限長直線銅線と一辺がaの正三角形のループコイルが同一平面にdはなれて置かれている.直線導線には,I=Iosin(2πft)の正弦波電流が流れている.ループコイルに流れる電流の振幅はioであった.ループコイルの抵抗はRで,自己インダクタンスは無視できる. ?電流Iが作る磁束密度の分布を求めよ ?正三角形のループコイルに誘起される誘導起電力の振幅をIoを用いて表せ ?直線導体上の電流の振幅Ioをioを用いて表せ
この場合の,条件をどのように活用していけば,いいのかペンが進みません. 聞いてばかりですみませんが,もう少しだけアドバイスを頂けると嬉しいです.
ちなみに,この問題の難易度をレベル1〜5で表すと,どれにあたりますか?
Re: 電磁誘導
yama さんのレス (2009/08/23(Sun) 01:01)
磁束 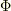 は
は 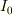 に比例するので,誘導起電力
に比例するので,誘導起電力
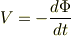
を計算すると
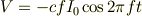
の形の式になるはずです.ただし  は
は  や
や 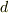 で表される定数であり,
で表される定数であり, 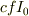 が誘導起電力の振幅です.
が誘導起電力の振幅です.
ループコイルに流れる電流の振幅はオームの法則により
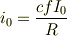
となるので,これから逆に 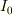 を
を 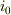 で表すことができます.
で表すことができます.
問題の難易度については,どんな基準で評価するのかよく分からないので何とも言えませんが,特に難しいものだとは感じられません. 磁束を求めるのがやや難しいかもしれませんが,それ以外は基本的なことが分かっていれば簡単だと思います.