RC=ρεの導出
RC=ρεの導出
ぶどう さんの書込 (2009/08/17(Mon) 10:03)
学部4年です.
正負等量の電荷を持つ二つの導体間の電気容量をC,二つの導体間の合成抵抗をR,二つの導体間の媒質の誘電率をε,抵抗率をρとすると,RC=ρεなる関係が成り立つことが教科書(詳解 電気磁気学例題演習,山口勝也,コロナ社,p.175)に記載されていますが,肝心の導出部分が書いてありません.
電極の形状や配置が任意の場合について,この式を導くにはどうしたらよろしいでしょうか?ご教授お願いします.
Re: RC=ρεの導出
toorisugari no Hiro さんのレス (2009/08/17(Mon) 11:57)
私も計算したことないので,つなぎです.
> 電極の形状や配置が任意の場合について,この式を導くにはどうしたらよろしいでしょうか?ご教授お願いします.
平板の場合は分かるのですね? 一般の場合は大変ですね.
とりあえず,静電ポテンシャルを  ,電流密度を
,電流密度を 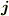 ,電束密度を
,電束密度を 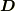 として,これらの間の関係式を求めてください.
として,これらの間の関係式を求めてください.
Re: RC=ρεの導出
mNeji さんのレス (2009/08/17(Mon) 15:51)
極論すれば,平行板コンデンサに挟まれた「誘電体」が,同時に「導電体」であるということですが,このような状況はあるのでしょうかね.なにか特殊な気がしますが.
Re: RC=ρεの導出
toorisugari no Hiro さんのレス (2009/08/17(Mon) 16:08)
> 平行板コンデンサに挟まれた「誘電体」が,同時に「導電体」であるということですが,このような状況はあるのでしょうかね.なにか特殊な気がしますが.
もちろん,こういう状況も考えられるでしょうが,私は別物と考えていました.つまり,2つの金属塊が配置されているとき,周りの空間に誘電率  の誘電体を充填してできるコンデンサの容量
の誘電体を充填してできるコンデンサの容量 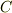 は,代わりに抵抗率
は,代わりに抵抗率  の導体を充填したときの抵抗
の導体を充填したときの抵抗  から
から
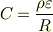
で求めることができる.つまり,コンデンサのgeometryの情報を 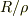 に隠すことができるということです.
に隠すことができるということです.
Re: RC=ρεの導出
mNeji さんのレス (2009/08/17(Mon) 16:37)
>つまり,コンデンサのgeometryの情報を 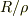 に隠すことができるということです.
に隠すことができるということです.
あ,そう考える方が自然かも知れませんね.ただ,ぶどうさんの記述; >二つの導体間の媒質の誘電率をε,抵抗率をρとすると,
を拝見した時に,ある媒質の「誘電率をε,抵抗率をρ」と考えるのかと感じました.
Re: RC=ρεの導出
ぶどう(質問者) さんのレス (2009/08/17(Mon) 16:46)
ありがとうございました.途中でベクトルとスカラがごっちゃになっていますが,導出でき,すっきりしました.Texに手間取って返信が遅くなりましたが,yama様,修正までありがとうございます.
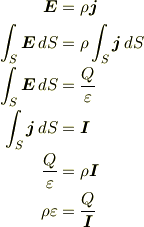
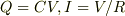 より
より
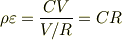
Re: RC=ρεの導出
yama さんのレス (2009/08/17(Mon) 17:15)
質問文からは,媒質が誘電率をεと抵抗率ρを持つように読みとれますが,toorisugari no Hiroさんが述べられたことも成り立つと思います. 導体間の電位差を一定に保つとき,媒質が誘電体であろうと導電体であろうと,媒質中の電場の分布は同じになるからです.
Re: RC=ρεの導出
ぶどう(質問者) さんのレス (2009/08/17(Mon) 17:57)
toorisugari no Hiro様,mNeji様,yama様 私の理解では,媒質が分極しつつ,電流を通すと考えておりました. 分布定数回路における,2導体間のコンダクタンス(漏洩抵抗)とキャパシタンスのようなイメージです.分布定数回路におけるコンダクタンスは主に媒質中の水などの不純物によるものですので,同じとは言い切れませんが.
例えば,食塩水のような電解質では分極と電気伝導が同時に起こります. 平衡状態においては,電流が流れないという条件からρが無限大でなければ電界が0になりますが,非平衡状態では2導体の電荷により媒質中に電界が生じ分極をしつつ,ρに応じて電流が流れるということです.
Re: RC=ρεの導出
mNeji さんのレス (2009/08/17(Mon) 18:52)
>例えば,食塩水のような電解質では分極と電気伝導が同時に起こります.
なるほど,電解質溶液は考えませんでしたが,電解液の場合,電場は主として電極近傍の二重層に局所化されますね.電気分解が発生しない程度の交流応答としてモデル化するのでしょうか....
Re: RC=ρεの導出
ぶどう(質問者) さんのレス (2009/08/18(Tue) 17:33)
mNeji様 電気分解は考慮しておりませんでした.アルミ電界コンデンサの漏れ電流から派生したイメージでしたが,私自身がよく理解していないためにうまく説明ができていませんでしたね.
mNeji様のイメージでは, 材料に電流が流れれば(ρ有限),逆起電力により外部電界が相殺されて分極は起こらない. すなわち 帯電している→電流は0→ρは∞. ということでよろしいでしょうか.
私のイメージは,その中間が存在するというものです. 伝導帯の電子が電流に寄与しつつ,荷電子帯の電子が分極するような...
あくまで私の想像ですので,有限の誘電率と抵抗率を持つような材料があるのか,計算上成り立つだけで実在しないモデルなのか,学校の夏季休暇が空けたら教授に聞いて勉強したいと思います.現在私に議論できるだけの知識と理解がなくお待たせしてしまいますが,休暇が終わる10月はじめにスレッドを立てたいと思いますので,お時間があればお付き合いください.
Re: RC=ρεの導出
mNeji さんのレス (2009/08/19(Wed) 00:51)
>材料に電流が流れれば(ρ有限),逆起電力により外部電界が相殺されて分極は起こらない. >すなわち >帯電している→電流は0→ρは∞. >ということでよろしいでしょうか.
少なくとも電極表面近傍の限られた領域に電場勾配の大半が存在して,中間領域には弱い電場勾配で,かつイオン伝導ですね.ただ,電極反応が判らないと,定量的な論議はできないような気がします.
講義で判ったら,ご紹介をして下さい.
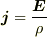 を1つの導体を囲む閉曲面上で積分することによって簡単に導くことができますね.
を1つの導体を囲む閉曲面上で積分することによって簡単に導くことができますね.