確認してもらえませんか？

花鳥風月さんの書込 (2009/08/15(Sat) 12:07)

お久しぶりでございます．

反応速度の問題をやっていて，答えが一致しません．どこがいけないのか見ていただけませんか？

問題エタンの熱分解は一次反応であって，次のような各温度における反応速度定数を得た．これより，活性化エネルギーと頻度因子を求めよ．ｔ（℃）550570590610630 ｋ*10＾5（/ｓ）2.58.223.157.6141.5

僕のやり方ｔ＝550℃と610℃に注目して， ln57.6 =lnA-E/883R ln2.5 =lnA-E/823R より，E=316ｋJとなりましたが，解答では，301ｋJとなっています．どこがいけないのでしょうか？

用いるデータによって違いが生じると思います． 570℃と610℃の値を用いると301ｋJになるようです．最も適切な方法は，すべてのデータを用いて最小自乗法によって最確値を求めることでしょうね．

選ぶデータによって誤差が生じていたのですね．最小二乗法かあ．なかなか大変ですね,,,．有難うございます．直接の疑問は解決できました．

失礼します．

測定点が５つあります．どの値を使うかはまずグラフを書いてから決まることです．

ｌｎ(ｋ)と１／Ｔで書くと直線になるはずの式です．書いてみると少し上に湾曲しています．最小自乗法を使うかどうかは別にして直線に載っていることの確認は必要です．両端の値を使うと頭から決めてしまうのは間違いです．２番目と４番目を使うというのはグラフを書いてみての選択です．

最初のデータの２．５という数字が精度不足であるということから外すという判断も成り立ちます．

この程度のデータ数だと判断は難しいですね．機械的に最小二乗法で計算すると

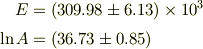
$E &= (309.98 \pm 6.13)\times 10^3\\\ln{A} &=(36.73 \pm 0.85)$

となり，

> より，E=316ｋJとなりましたが，解答では，301ｋJとなっています．

花鳥風月さんの方がぎりぎりレンジ内です．(別に最小二乗法が正しいという意味ではありません．)

そもそも，これはfactor 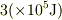$3(\times10^5\text{J})$ が合えば十分（せいぜい有効数字2桁 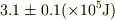$3.1\pm 0.1(\times10^5\text{J})$ ）といった精度の問題だと思います．