基底の変換の疑問

基底の変換の疑問

ＫＥＮ さんの書込 (2009/08/14(Fri) 00:54)

こんばんは．相対性理論をひとりで勉強している者です．テンソルのところで大きくつまずき，ベクトルからやり直しています．反変，共変ベクトルあたりでまたうろうろしています．そんなとき，「物理のかぎしっぽ」をみつけました．プリントして勉強を始めました． 「ベクトル解析」の「ベクトル代数２」の「基底の座標変換」の２ページ目の（１）と（２）式（ｅとｅダッシュの変換の式）はどう考えても同じ式としか思えません．（１）＝（２）で，すなわちｅとｅダッシュが等しい．つまり，座標がまったく変換されていないと思うのですが・・・・・．添え字の見方が間違っているのでしょうか．どうぞ，ご教示ください．

Re: 基底の変換の疑問

Yokkun さんのレス (2009/08/14(Fri) 08:13)

\alpha_{i^\prime}^k と \alpha_k^{l^\prime} とは同じ \alpha を使っているので紛らわしいですが，異なる変換係数であり，互いに逆行列の関係になっているのですね．ここで \alpha には「変換係数」という共通の意味だけが込められていて，添え字のプライムの位置でその実際の変換の向きを区別しているのです．１次変換では，

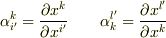\alpha_{i^\prime}^k=\frac{\partial x^k}{\partial x^{i^\prime}} \qquad \alpha_k^{l^\prime}=\frac{\partial x^{l^\prime}}{\partial x^k} といった具合です．ただし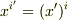， x^{i^\prime}=(x^\prime)^i の意味です．

Re: 基底の変換の疑問

ＫＥＮ さんのレス (2009/08/14(Fri) 18:30)

ｙｏｋｋｕｎ様 早速にご回答をいただき感激しています．こんな状態なので，勉強するほどどんどん後退して行くことがしょっちゅうです． 添え字の「プライム」も初めて見るもので，?だったのですが意味がわかりました．これで，つぎの（３），（４）を比べる意味もよくわかります．ひきつづき，このテキストで勉強し，共変，反変ベクトルのところへ進みたいです． ありがとうございました．