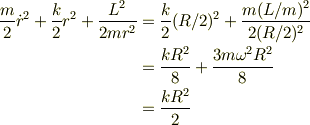物体の描く軌道
物体の描く軌道
リコモン さんの書込 (2009/08/13(Thu) 02:07)
原点 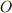 に対して大きさの無視できる物体
に対して大きさの無視できる物体 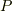 (質量
(質量  )の位置を
)の位置を 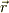 とし,
とし, 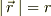 としたとき,
としたとき,  を定数として,下の方程式に従って運動する物体がある.
を定数として,下の方程式に従って運動する物体がある.
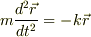 ,すなわち
,すなわち 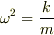 としたとき,
としたとき, 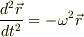 ここで2つの実験を行った
《実験1》:
ここで2つの実験を行った
《実験1》: 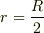 の位置から物体を
の位置から物体を 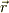 方向に初速度
方向に初速度 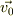 で運動させたら,振幅が
で運動させたら,振幅が  で原点を中心とした,単振動をした.
で原点を中心とした,単振動をした.
《実験2》: 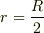 の位置から物体を
の位置から物体を 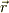 と垂直な方向に同じ初速度
と垂直な方向に同じ初速度 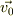 で運動させた.
そのとき,《実験2》で物体はどのような軌道を描くか?
で運動させた.
そのとき,《実験2》で物体はどのような軌道を描くか?
**********************************\
という問題があるのですが,まず, 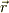 における物体の位置エネルギーは
における物体の位置エネルギーは 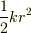 で表されますから《実験1》でエネルギー保存より(
で表されますから《実験1》でエネルギー保存より( 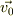 の絶対値を
の絶対値を 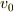 として)
として)
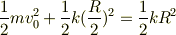
よって,
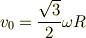
とでたのですが,ここから先がわかりません. おそらく楕円軌道を描くと思うのですが,どのように解けばよいのでしょうか?
どなたかわかる方がいらっしゃったら,お手数ですが,お考えください.
Re: 物体の描く軌道
mNeji さんのレス (2009/08/13(Thu) 10:37)
二次元での極座標表示にしてみたら如何でしょうか?
単位ヴェクタの表現としては「極座標,マジンガさん,のNo.25224スレッド」が参考になると思います.
ただ,2次元という意味では,z軸についての回転と考えて,
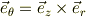
と置いてしまうのも,簡便かも知れません.
Re: 物体の描く軌道
リコモン さんのレス (2009/08/13(Thu) 15:03)
すみません.単純に座標を 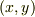 とおいたらできました.
とおいたらできました.
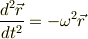
初期条件を 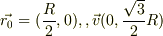 とおいて解いたら
とおいて解いたら
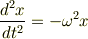
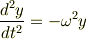
これを解いて
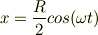
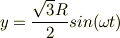
となって楕円軌道を描きました.
すると,x成分,y成分それぞれ独立してエネルギー保存則の形をした保存する式が立てられますが,それらもエネルギー保存の式なのでしょうか?
Re: 物体の描く軌道
mNeji さんのレス (2009/08/13(Thu) 15:29)
>それらもエネルギー保存の式なのでしょうか?
そう思いますが,折角,回転運動と考えられたのですから,中心力では角運動量が保存されますよね.
Re: 物体の描く軌道
リコモン さんのレス (2009/08/18(Tue) 17:55)
いままで,極座標でのニュートンの運動方程式はサボってましたがこのさい自分なりにいろいろ勉強できました. mNejiさんご返答ありがとうございました.
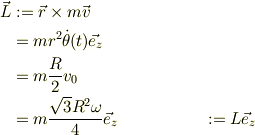
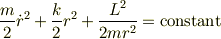
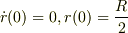 より,
より,