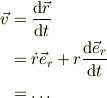極座標
極座標
マジンガ さんの書込 (2009/08/12(Wed) 13:58)
:動径
の増大する向きにとった単位ベクトル
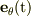 :天頂角
:天頂角  の増大する向きにとった単位ベクトル
の増大する向きにとった単位ベクトル
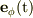 :方位角
:方位角  の増大する向きにとった単位ベクトル
の増大する向きにとった単位ベクトル
デカルト座標と極座標の関係
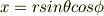
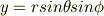
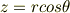
これをデカルト座標系における 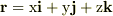 に代入すると
に代入すると

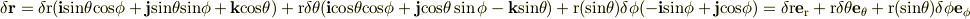
座標軸間の関係
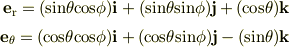
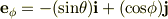
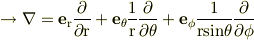
極座標の座標軸の時間変化
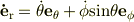
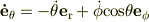
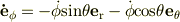
すなわち
![\frac{d}{dt}\left[\begin{array}{ccc}\bf e \rm _r \\\bf e \rm _\theta \\\bf e \rm _\phi \\\end{array}\right]=\left[\begin{array}{ccc}0 & \dot{\theta} & \dot{\phi}sin\theta \\-\dot{\theta} & 0 & \dot{\phi}cos\theta \\-\dot{\phi}sin\theta & -\dot{\phi}cos\theta & 0 \\\end{array}\right]\left[\begin{array}{ccc}\bf e \rm _r \\\bf e \rm _\theta \\\bf e \rm _\phi \\\end{array}\right]](http://hooktail.maxwell.jp/bbslog/f1204be207e1c145d5a52921234bdc1d.png)
よって,
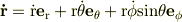
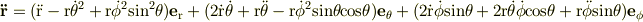
【問題】 極座標系での速度及び加速度ベクトルが上のように表せることを示せ.
プリントにこのような問題があるんですがプリントに書いてあるのがそのまま答えな気もしますが,いまいち理解できません.
「座標軸間の関係」からわからないです.何故 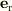 ,
, 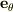 ,
, 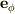 が上のようになるのか…
が上のようになるのか…
Re: 極座標
マジンガ さんのレス (2009/08/13(Thu) 14:45)
お二方ありがとうございます.
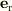 などはそのように定義されてたんですね;
などはそのように定義されてたんですね;
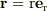 は確かに忘れてました(汗
は確かに忘れてました(汗
Re: 極座標
mNeji さんのレス (2009/08/14(Fri) 09:40)
toorisugari no Hiroさん,
No.25225をじっと見せて頂きました.こう考えると,それぞれの方向微分の意味が良く判りました.
#長い事,緊急の場合(急にノート計算する時に)作図しながら出してました.
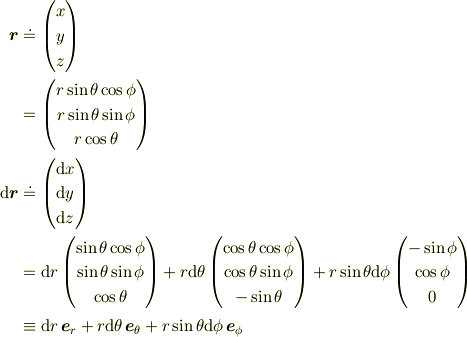
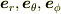 は
は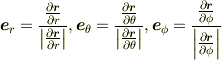
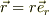 を忘れていませんか?
を忘れていませんか?