一次元熱伝導方程式について
一次元熱伝導方程式について
光太郎 さんの書込 (2009/08/11(Tue) 15:17)
こんにちは.学部4年の光太郎といいます.
大学院の過去問を解いていたら,分からない問題が出できたのでみなさんのお力をかりたく相談に来ました. 前に同じ問題をここで相談しましたが,自分の努力不足と皆様の回答が 専門的すぎて理解できませんでした. なので,専門的な言葉をあまり使わないでもらえると非常に助かります.
【問題文】 長さ1(m)の棒の一次元熱伝導を考える.時間をt(s),棒の一次元座標をx(m)とする.初期状態において棒の温度Tは一様に0(℃)である.t=0(s)で,棒の左端の温度が瞬間的に50(℃)に引き上げられ,その後は,その温度で維持される.棒右端の温度は0(℃)一定である.次の一次元の熱伝導方程式を用いて以下の問いに答えよ.
∂T/∂x=a^(2)∂^(2)T/∂x^(2)
【問題】 T(x,t)=A(x)B(t)と置き,二つの常微分方程式に変換しなさい.また,与えれられた境界条件と初期条件の下で解きなさい.
【分らない点】 まず,最初に境界条件を考えると,以下の二つの条件が出てきます. T(0,t)=A(0)B(t)=50・・・(1) T(1,t)=A(1)B(t)=0・・・(2)
(1)について,A(0)≠0より, B(t)=50/A(0)となり,B(t)は定数となります. この物理的意味は,温度Tは時間に関係なく距離のみに 依存するとなります.
しかし,以下の点でこれは矛盾しています. x=1/2についてt=0とt=t1のそれぞれの時について考える. ・t=0の時,x=1/2では温度0 ・t=t1の時は,x=1/2では温度は0かもしれないし,そうでないかもしれない.
よって,Tは時間にも依存するします. なので,上記のように矛盾が起きるのですが, これはどこがいけないのでしょうか?
長くなりましたが,よろしくお願いします.
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/11(Tue) 17:07)
> これはどこがいけないのでしょうか?
問題が間違っているからです.初期条件が三角関数で境界条件が単純なものならともかく,このような境界条件,初期条件の問題が変数分離系になるわけがありません(重ね合わせなら,まだ分かります).矛盾はスレ主さんが出していますね.
Re: 一次元熱伝導方程式について
光太郎 さんのレス (2009/08/11(Tue) 17:19)
toorisugari no Hiro様
コメントありがとうございます.
問題が間違っているというのは, 出題者のミス,つまり問題文の状況が 物理的にあり得ないということなのでしょうか?
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/11(Tue) 17:32)
>物理的にあり得ないということなのでしょうか?
物理的にあり得ますが,解法が間違い.正しい解法は前スレを参考にしてください.
Re: 一次元熱伝導方程式について
光太郎 さんのレス (2009/08/11(Tue) 19:42)
Toorisugari no hiro様
コメントありがとうございます.
問題に従って変数分離して解いたつもりなのですが,具体的にどこが間違っているのでしょうか?
また,前スレの解法は問題のT(x,t)=A(x)B(t)の変数分離をしていないので,問題文にのっとった解法を知りたいと思いましす.
よろしくお願いします.
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/11(Tue) 19:53)
変数分離ではとけません.そういう意味で「問題はまちがっています.」
『変数分離』を「好意的」に
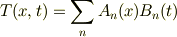
と解釈して(さらに定常解を取り出し,残りを比較的簡単な正弦関数展開で解けると仮定して),問題を解いたものが前スレです.
Re: 一次元熱伝導方程式について
mNeji さんのレス (2009/08/12(Wed) 16:46)
横から失礼します.
私は昔から熱伝導タイプの問題が苦手なので,ついに参考書を眺めて見ました;
理工系の基礎数学 4, 偏微分方程式, 及川 正行・著, 岩波書店, ISBN4-00-007974-3
この「第3章熱伝導方程式,3.1節 有限な長さの棒における熱伝導」の解説の先頭部分を引用しますと;
〜〜〜〜引用開始〜〜〜〜〜〜
左端 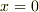 では一定温度
では一定温度 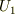 に保たれ,右端
に保たれ,右端 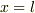 では一定温度
では一定温度 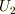 に保たれている長さ Lの棒における熱伝導を考えよう.これは次の様な混合問題になる.(
に保たれている長さ Lの棒における熱伝導を考えよう.これは次の様な混合問題になる.(  は正の定数)
は正の定数)
熱伝導方程式 : 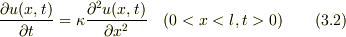 初期条件:
初期条件: 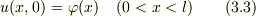 境界条件:
境界条件: 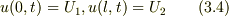
(以下略) 〜〜〜〜引用終了〜〜〜〜〜〜
とあります.
今回の問題は「初期条件」が明示的に与えられて無く,事実上,
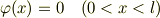
となっていて,ゼロ解になっているような気がしますが?
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/12(Wed) 17:03)
> ゼロ解になっているような気がしますが?
そうですよ.問題あるのでしょうか?
解は
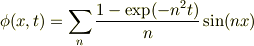
型のものが得られますが,これは初期条件をみたしますよね.
Re: 一次元熱伝導方程式について
mNeji さんのレス (2009/08/12(Wed) 18:18)
>型のものが得られますが,これは初期条件をみたしますよね.
なにか,答えが先にでてきてしまったような感じがして,とても居心地が悪いのですが....
#やっぱり,拡散型の方程式は理解しずらい!!!
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/12(Wed) 18:47)
> なにか,答えが先にでてきてしまったような感じがして,とても居心地が悪いのですが....
いや,既に前スレで答えが出ている話だから...
# あ,論理展開の話?
Re: 一次元熱伝導方程式について
mNeji さんのレス (2009/08/13(Thu) 10:52)
toorisugari no Hiroさん,
>いや,既に前スレで答えが出ている話だから... ># あ,論理展開の話?
多分そうかも知れません.私は気長に勉強中(現在は,常微分方程式を再勉強中で,偏微分方程式はまだ蚊帳の外)ですし,フーリエ級数展開もやや苦手(判った所から直ぐ忘れる)なので,自信を持って発言出来ません.
恐らく,これまでのご発言を丁寧にフォローすればいいのでしょうが,私の脳裏には断片的で良く判らないというところです.
結局, (1)定常解は,常微分方程式でいうと強制解に相当し, (2)変数分離解は,常微分方程式でいうと自由解に相当し, (3)定常解をフーリエ級数展開して,自由解と足し合わせる. といった流れなのでしょうかね?
それにしても,定常解が,瞬間に発生するというのはとても想像ができません(泣).
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/16(Sun) 18:32)
> 結局, > (1)定常解は,常微分方程式でいうと強制解に相当し, > (2)変数分離解は,常微分方程式でいうと自由解に相当し, > (3)定常解をフーリエ級数展開して,自由解と足し合わせる. > といった流れなのでしょうかね?
強制解と言えるかはともかく,大筋であっています. この問題が難しいのは定常解が正弦関数の単色波(0固有値モード)ではなく,また正弦関数で展開すると特異点を持つことです.
問題を簡単化して
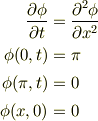
としましょう. 解を
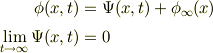
とします.
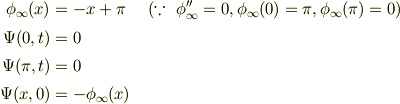
となるので,
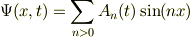
と仮定します.
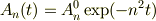
なら
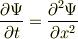
を満たします.
ここで,
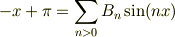
と仮定し,
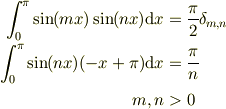
より, 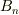 が求まり,
が求まり,
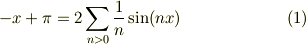
となるから,
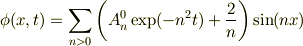
が得られ,初期条件を適用して
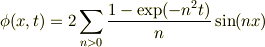
が得られます.
ただし,(1)式が原点で特異点をもつことと絡んで, 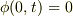 となり,境界条件は満たしません.
この辺り,前スレッドでも述べたように,本当に正弦関数で展開できるのか?という話です.
となり,境界条件は満たしません.
この辺り,前スレッドでも述べたように,本当に正弦関数で展開できるのか?という話です.
# 追加 なお,
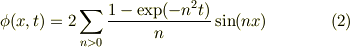
ではなく,(1)を考慮して
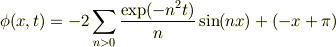
とおくと, 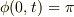 となり,境界条件は満たします.
ただ,これは(2)式が
となり,境界条件は満たします.
ただ,これは(2)式が 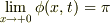 を満たすので,特異点を形式的に除去したに過ぎないと思います.
を満たすので,特異点を形式的に除去したに過ぎないと思います.
Re: 一次元熱伝導方程式について
mNeji さんのレス (2009/08/16(Sun) 19:31)
toorisugari no Hiroさん,
ご丁寧な解説を感謝します.
これを念頭において,すこし先に偏微分方程式の再復習したいと思います.
なお,フーリエ級数展開を正弦波で展開されていますが,余弦波で展開すると不都合な理由はなにでしょうか?
Re: 一次元熱伝導方程式について
toorisugari no Hiro さんのレス (2009/08/17(Mon) 08:49)
> 余弦波で展開すると不都合な理由はなにでしょうか?
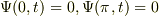 を満たす三角関数を普通は正弦関数といいますよね:-)
を満たす三角関数を普通は正弦関数といいますよね:-)
# そうでなく,「境界条件を満たさない基本モードで展開してもいいはずなのに,しない理由は?」ということでしょうか?それなら,「難しいから.」
Re: 一次元熱伝導方程式について
mNeji さんのレス (2009/08/18(Tue) 17:20)
toorisugari no Hiroさん,
長い事掛かりましたが,やっ〜〜〜と理解出来る様になりました.
今回,トラップされたのは;
(1)初期条件: 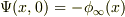 (2)定常解の正弦波展開:
(2)定常解の正弦波展開: 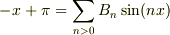
の2点でした.
(1)は,境界条件との関係があやふやだったことにより,単純に静止状態から始めるという事を認める事が出来なかった要です.これと(2)が絡んで,頭が固着していたと思います.
(2)は,「0<=x<=L」のタイプで正弦波展開すると,「x=0」でギャップを生じるので宜しくないと思い込んでいました.この場合,「x→+0」で考えればいいのに気付きました.
でも,私としては,余弦波展開のほうが理解し易いので「-L<=x<=L」として,定常解を;
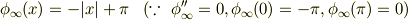
とする方向で,考え直してみたいと思います.ついては,フーリエ級数展開を確実にするべく再勉強しています.
長い事,気長に付き合ってくださって,有り難うございました.