ローレンツ収縮
ローレンツ収縮
けん(大学4年) さんの書込 (2009/08/08(Sat) 00:33)
ローレンツ収縮に関する質問です.
周長lの円状の道に,長さlのひもを置いたとします. ある時刻に円の中心から光を発し,その光がひもに到着したとき,ひもは円周上を左回りに回り始め,ある速さになったら加速をやめるとします.このとき,円状の道とひもの長さの関係はどうなっているのでしょうか.静止系(道の系)から見ると,ローレンツ収縮により,ひもは短く見えると思うのですが,円の半径の方向にはひもは運動していないため,ひもの半径は変わらないように思います.
等速度運動する一次元の棒を静止系から観測する場合には,静止系で棒の端を観測するときの2つの時空点が静止系で同時刻でも棒の系では同時刻ではない,というのが本質ですが,上の問題では何が本質になっているのでしょうか.
よろしくお願いします.
Re: ローレンツ収縮
toorisugari no Hiro さんのレス (2009/08/08(Sat) 12:02)
ああ,この問題ですか.やっかいですね. とりあえず,質問に質問で返します.次の問題を考えてください.
「ある慣性系Aにおいて,2台の同じ性能のロケットが距離  をおいてある直線上を並んで静止している.ロケットの方向は直線に平行で同じ向きを向いている.このロケットが(Aからみて)同時に点火しその後(Aからみて)同時に点火をやめ,直線上を並んで共に速度
をおいてある直線上を並んで静止している.ロケットの方向は直線に平行で同じ向きを向いている.このロケットが(Aからみて)同時に点火しその後(Aからみて)同時に点火をやめ,直線上を並んで共に速度  の慣性飛行状態に入った.そのときのふたつのロケット間の(Aからみた)距離を求めよ.」
の慣性飛行状態に入った.そのときのふたつのロケット間の(Aからみた)距離を求めよ.」
答えは  です.
#
です.
# 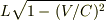 でありません.
でありません.
理由を考えてください.
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/08(Sat) 22:48)
レスありがとうございます.
二つのロケットの間に物はなく,空間だから,Lなのでしょうか. でも二つのロケットをひもでつないだらそのひももロケットと同じ割合で収縮して見えるはずです.
静止系(慣性系A)で距離L離して出発した長さLの二つのロケットと 静止系(慣性系A)で距離Lのひもでつないで出発した長さLの二つのロケット を考えた場合に,前のロケットの先端から後ろのロケットの後端までの距離は前者の方が短い,ということを主張しているわけですね.
等速度運動する慣性系のローレンツ収縮については,ものさしを運動させるイメージを持っています. ローレンツ収縮は,物体があって初めて起こるものなのですか?
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/09(Sun) 00:03)
けんさん,はじめまして. 私もよく理解しておらず,先の展開が楽しみなので参加させてください.
>ローレンツ収縮は,物体があって初めて起こるものなのですか?
そんなことはないでしょうね?実際の座標系の設定と測定には何らかの物体が必要だとは思いますが.
ローレンツ収縮は,「同時性」の問題とつねにリンクしています.その辺はどうでしょう?
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/09(Sun) 00:22)
>Yokkunさん
はじめまして.ぜひ議論に加わってください.
>実際の座標系の設定と測定には何らかの物体が必要
これが大事な気がします.
toorisugari no Hiroさんが提起された問題の場合,ロケットという物体は用意したが,その間の空間は…?ということの気がします.
Re: ローレンツ収縮
toorisugari no Hiro さんのレス (2009/08/09(Sun) 12:01)
# あれ,トビラ..さんが反応していないぞ. # ま,彼が出てきたら交代するとして,
元の問題はかなり難しい問題です. 易しい問題を考えた方が良いと思います.
>>「ある慣性系Aにおいて,2台の同じ性能の
...
>> そのときのふたつのロケット間の(Aからみた)距離を求めよ.」
>> 答えは  です.
です.
になるのは,以下の理由からです.
運動方程式は空間平行移動で不変. よって,A系でみたロケットの加速度は同じだから,A系でみたロケットの速度は常に同じ.よって,A系でみたロケット間の距離は変化しない.
当たり前です.
でも,ローレンツ収縮はどこへ行ったのでしょう.
> ローレンツ収縮は,物体があって初めて起こるものなのですか?
まさか.
実際,ちゃんとローレンツ収縮は起きています.
慣性系からみたロケットの間隔は  ですが,
ロケットからみたロケットの間隔は
ですが,
ロケットからみたロケットの間隔は 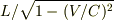 です.
です.
つまり,ロケットの固有な間隔が延びています.
それが慣性系から観測されるとローレンツ収縮を起こして 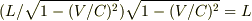 に観測されるのです.
に観測されるのです.
じゃあ,なぜ,ロケットの固有な間隔が延びるのでしょうか?
考えてみてください.加速度が重要な働きをしていますが,本質的には「同時の相対性」を考えれば特殊相対論の範囲で理解できます.
ヒント:前のロケットが加速して微小な速度を持ったとき,「前のロケットからみた同時刻」の後ろのロケットは,どんな状態にあるでしょうか?同じ速度に達してるしょうか?
# 加速度  で加速中のロケットの軌道は近似的には
で加速中のロケットの軌道は近似的には 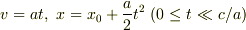 と考えられるので,軌道の接線を光円錐に対して折り返せば,「同時刻」の線が得られますね.
と考えられるので,軌道の接線を光円錐に対して折り返せば,「同時刻」の線が得られますね.
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/09(Sun) 18:30)
>toorisugari no Hiroさん
何だかよく分からなくなってきました.
> >>「ある慣性系Aにおいて,2台の同じ性能の ... >> そのときのふたつのロケット間の(Aからみた)距離を求めよ.」 >> 答えはLです.
になるのは,以下の理由からです.
運動方程式は空間平行移動で不変. よって,A系でみたロケットの加速度は同じだから,A系でみたロケットの速度は常に同じ.よって,A系でみたロケット間の距離は変化しない.
これについてですが.同様に, A系でみた一つのロケットの先端と後端の加速度は同じだから,A系でみたロケットの先端と後端の速度は常に同じ.だから,A系でみたロケットの先端と後端の間の距離は変化しない.つまりロケットの長さは変化しない.
といえると思うのですが,これだとロケットの長さが変わっていません.どこかに間違いがあるのでしょうか.どこでしょうか.
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/09(Sun) 19:21)
>A系でみた一つのロケットの先端と後端の加速度は同じだから,A系でみたロケットの先端と後端の速度は常に同じ.
もし,この条件であればA系で見た長さは静止時と変わらないことがいえると思います.間違っていないと思いますよ.ロケット系で見たロケットの固有長が伸びたということになると思います.ちょっとびっくり.
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/09(Sun) 19:49)
得るべき結論は縮んで見える,ということなんじゃないでしょうか.ローレンツ収縮なので. それに,これが合っているとすると,ロケットの系では,まわりが加速度運動したら自分たちが縮んでしまった,というおかしなことになっています.
Re: ローレンツ収縮
ミュフ猫 さんのレス (2009/08/09(Sun) 20:10)
けん(大学4年)さん,こんばんは.
上記のサイトが参考になるかと思います.
toorisugari no Hiroさん,ごめんなさい. 我慢できずに,しゃしゃり出て来ました.(T_T) けんさん,Yokkunさんのために,書き込みを続けてください.m(_ _)m 教えてもらう人にとって,成熟したスキルをお持ちのtoorisugari no Hiroさん, yamaさん等の方々に教わる方が,有り難いに決まってますから. 未熟と知りながら,口を出したくなるんですよ. 特に私のようなスキルの低い物理学ミーハーは.(T_T)
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/09(Sun) 20:11)
# 加速度aで加速中のロケットの軌道は近似的には・・・と考えられるので,軌道の接線を光円錐に対して折り返せば,「同時刻」の線が得られますね.
けんさん,これ考えてみましたか? A系から見て常に前後ともに等しい速度である加速中のロケットの場合,ロケット系から見ると,前後の速度は等しくありません.同じ理由で,ロケット系から見たロケットの長さは伸びて見えることになると思います.
Re: ローレンツ収縮
ミュフ猫 さんのレス (2009/08/09(Sun) 22:16)
特殊相対性理論での剛体の定義を,考え直すべきかもしれませんね. 例えば, 「運動物体のうち,その瞬間静止系において形状を変えないもの.」 とか.
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/09(Sun) 22:38)
ちょっと余談ですが,ちょん切れたレールから電車が落ちるか否か・・・というパラドックスもありましたよね.ある本で紹介されたその説明の中で,「相対論では剛体はありえない」みたいな記述が,レールのすきまから曲がって落ちていく電車の図とともにあったんです.初めこれを見たときかなり違和感があったのですが,剛体上の位置による同時性が問題になればまさしく剛体の定義に関わってくることになりますね.
Re: ローレンツ収縮
ミュフ猫 さんのレス (2009/08/09(Sun) 23:00)
>剛体上の位置による同時性が問題になればまさしく剛体の定義に >関わってくることになりますね.
そう思います.でも,「剛体はありえない」かどうかは微妙かと. というのも,ローレンツ収縮によりいくら縮んで見えても,その剛体に内部応力が 生じてなければ,「見かけ」の収縮とも解釈できますから.
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/09(Sun) 23:49)
>ローレンツ収縮によりいくら縮んで見えても,その剛体に内部応力が 生じてなければ,「見かけ」の収縮とも解釈できますから.
そうなんですね.ですからその本の記述にはちょっと違和感を覚えたんです. でも,ローレンツ短縮した列車が曲がってすきまから落ちていく・・・というその本の挿絵の意味は最近になってようやくわかってきた気がします.このパラドックスの説明では,条件もあいまいで説明も十分とはいえないものでしたが.
Re: ローレンツ収縮
toorisugari no Hiro さんのレス (2009/08/10(Mon) 12:23)
> これだとロケットの長さが変わっていません.どこかに間違いがあるのでしょうか.どこでしょうか.
間違っていません.ただし,加速システム(ロケット噴射)の取り付け位置やロケットの弾性体的構造によって,ロケットの長さは地上からみて縮んだりあるいは延びたりするかもしれません.
ローレンツ収縮を習いはじめの人は,動いたら縮むと理解されていると思いますが,間違いです.
あくまでも,動いているロケット内部のあるものの長さを,地上で観察するとロケット系での値より縮んで見えるということであって, 止まっているものが動いていると縮む,とは言っていないことに注意してください.
加速度を含む問題は要注意ということですね.
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/10(Mon) 19:06)
>ミュフ猫さん
ありがとうございます.サイトの文章をちゃんと読んでからお返事します.
>Yokkunさん
長さは静止時と変わらないようです.僕が誤解してました.
>toorisugari no Hiroさん
ローレンツ収縮を知って3年あまりですが,誤解してました.加速度,厄介です.
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/11(Tue) 19:40)
で,この場合,加速が終わって速度一定に移行したらどうなるのでしょう?
>A系でみたロケットの速度は常に同じ.よって,A系でみたロケット間の距離は変化しない.
しかるに,ローレンツ収縮が起こっているからロケット系でみたロケット間の距離は伸びっぱなし?うーん,いまいち納得できていないなあ.
Re: ローレンツ収縮
toorisugari no Hiro さんのレス (2009/08/11(Tue) 19:57)
> ローレンツ収縮が起こっているからロケット系でみたロケット間の距離は伸びっぱなし?
そうです.
> うーん,いまいち納得できていないなあ.
どこら辺が?
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/11(Tue) 22:34)
時空ダイヤグラムから伸びていたのは,加速度運動で世界線が曲がったせいかと思ったのですが,そうではなかったのですか?曲がりがなくなったところから伸びがもどるような気がしたのです.ひょっとしてダイヤグラムのスケールのせいですか?
Re: ローレンツ収縮
yama さんのレス (2009/08/11(Tue) 23:17)
加速度を考えるとちょっと面倒そうですね. そこで一般の場合についてはtoorisugari no Hiroさんに説明していただくとして,問題を単純化して加速度が無限大の場合について考えてみました. すなわちA系で静止していた2台のロケットが,同時に初速度Vで等速直線運動を始めた場合を考えます.2台のロケットを1号および2号とし,2号が1号を追いかけるように動くものとします. 一方,A系に対して速度Vで動いているB系を考えます. A系でロケットが静止しているときは,B系ではロケットは逆向きの速度-Vで動いており,A系で速度Vで動いているときはB系では速度が0(すなわち静止)になります. ところが一般にA系で同時であってもB系では同時ではありません. つまり2台のロケットはA系では同時に動き出しますが,B系では同時には静止せず時間差をおいて静止します.この時間差の間にロケットの間隔が変化します.
詳しく見ていきましょう.
まずA系で2台が,静止しているとき,B系では2台は1号が2号を追いかけるように速度-Vで動いています.
2台の間隔がA系で  であるとすると,B系ではローレンツ収縮のため
であるとすると,B系ではローレンツ収縮のため 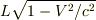 になっています.
A系では2台が同時に動き出しますが,B系ではまず1号が静止し少し遅れて2号が静止します.この時間差を
になっています.
A系では2台が同時に動き出しますが,B系ではまず1号が静止し少し遅れて2号が静止します.この時間差を  とすると,この間にロケットの間隔は
とすると,この間にロケットの間隔は 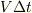 だけ広がることになります.
ローレンツ変換の公式によると
だけ広がることになります.
ローレンツ変換の公式によると 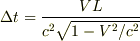 となるので,B系でのロケットの間隔は最終的には
となるので,B系でのロケットの間隔は最終的には 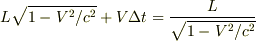 になるわけです.
になるわけです.
Re: ローレンツ収縮
Yokkun さんのレス (2009/08/12(Wed) 00:38)
yamaさん,ありがとうございます.
なるほど,時空ダイヤグラムで不連続に折れ曲がった世界線をまたぐB系の同時線の長さが伸びていくのが見て取れます.特殊相対論の範囲での考察では,世界線が連続的に曲がっていく場合もこの微小な変化が積み重なっていくと考えればいいんですね?
Re: ローレンツ収縮
yama さんのレス (2009/08/12(Wed) 09:01)
そうですね. 連続的な速度変化を,不連続な速度変化の積み重ねで近似し,それぞれの速度変化が無限小になった極限を考えればいいでしょうね.
Re: ローレンツ収縮
けん(大学4年) さんのレス (2009/08/18(Tue) 01:05)
みなさんのヒントを元にもう少し自分で考えて見ます. ありがとうございました. また質問させて頂くかもしれませんがそのときはよろしくお願いします.