若田さんが過ごした時間
若田さんが過ごした時間
Yokkun さんの書込 (2009/08/03(Mon) 23:36)
他のQ&Aサイトの疑問に対して,知っているつもりで計算しても,全く自信がもてません.
地上の時計の進みを  とするとき,速さ
とするとき,速さ  で運動する若田さんの腕時計の進み
で運動する若田さんの腕時計の進み 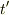 は,
は,
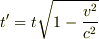
と計算されます.ここで  は光速(2.998×10^8m/s)です.すると,137日間7675m/sで飛び続けた若田さんの腕時計の遅れは,
は光速(2.998×10^8m/s)です.すると,137日間7675m/sで飛び続けた若田さんの腕時計の遅れは,
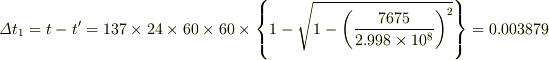 秒
秒
ということになります.一方,地上の重力による時間の遅れは,
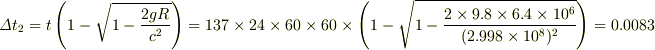 秒
秒
ただし,ここに  は重力加速度,
は重力加速度,  は地球半径,
は地球半径,  は光速です.
は光速です.
予想に反して相対速度による効果よりも大きくなりました. したがって,計算に間違いなければ若田さんの時計の方が進むことになりますね.
ただし, 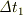 の計算が重力場の中で特殊相対論を使っていることも気になる所です.
の計算が重力場の中で特殊相対論を使っていることも気になる所です.
さて,長くなりましたが,若田さんの過ごした時間は地上に比べて実際進んだのか遅れたのかどっちなのでしょう?
Re: 若田さんが過ごした時間
なんとなく さんのレス (2009/08/04(Tue) 00:10)
なんとなくです. これは答えらしきものは知っていますが,質問ですか?答えは分かっていて問題を問いかけているのですか? まあ,どちらにしても遅れるが正しい,だと思います.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/04(Tue) 07:05)
なんとなくさん.レスありがとうございます. もちろん,質問です.答えもわかりません.
飛行機で周回して遅れを観測した古い実験は聞いたことがあります. しかし,この場合は重力の違いによる効果が無視できる高さでした. また,下のサイトにはそれらしい計算が載ってはいます.
重力による効果によって周回軌道上の方が進む例も挙げられています.しかし,重力の効果についてはステーション内は無重力として比較するべきではないかとも思います.この点がちょっとひっかかっています.
Re: 若田さんが過ごした時間
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/04(Tue) 08:51)
ミュフ猫さん,サイトの紹介ありがとうございます.
依然として気になるのは,衛星上では無重力で等価原理によればその重力ポテンシャルはゼロと評価すべきではないかということなのですが,どうなんでしょう?
Re: 若田さんが過ごした時間
なんとなく さんのレス (2009/08/04(Tue) 10:27)
>Yokkunさん
ここでもかなり論議されていましたが,私には難しすぎてよく分かりません. でも,この問題は人工衛星が重力ポテンシャル内で回転運動しているだけで,重力ポテンシャルが0に成るわけではないと思いますよ.人工衛星の上に立てば(つまり座標系を回転系に移れば),見かけの力である遠心力のため,力は釣り合い無重量となりますが,無重力ではありません.それより,時間を比較するのに,このように座標系を乗り変えては,相対的な時間を求めることに矛盾する気がします. 時間は無限遠の慣性系を基準として計算されているのだと思いますが,そこから見た運動を用いるのが正しいのではないでしょうか.このとき,人工衛星に働く力は重力のみで,自由落下しています.もし,回転運動であることの問題点があるとすれば,速度(ベクトルとして)を等速度運動としていることですが,これも人工衛星の質量が小さく特殊相対論で扱えることは,まあ問題ないでしょう.
等価原理はまさに人工衛星の上での座標系に移ったとき,観測者が重力を相殺する慣性力によって,その座標系内で局所慣性系となりうることだと思いますが,上記のように自信は無いですね(笑).
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/04(Tue) 10:44)
Yokkunさん
実は私も引っ掛かってます. ですが,この場合,公転運動による弱い慣性力で弱い重力を打ち消しているので, 地表から衛星軌道上までの狭い領域に限り,宇宙ステーション系の動径方向に おける時間のテンポのズレは,近似的にシュバルツシルト計量に従うと思います. (厳密には,回転系の効果が絡むはず.) なぜならば,公転運動における速度ベクトルが,常に動径方向に垂直になるから です. また,?t1の計算が重力場の中で特殊相対論を使っている理由は,以前の議論が 役立ちそうです. 近似的に静的とみなせる定常的な重力場において,すべての準拠点で同時刻空間 を共有するならば,二点間の固有時間比は三段論法で算出可能ではないでしょうか? つまり,赤道上の観測者A,赤道上を地球の自転周期で逆走する人B,赤道上空の 宇宙ステーション軌道上でBから見て静止するロケットC,宇宙ステーションDに おいて,それぞれの固有時間比は,
A⇔B特殊相対論ですれ違い様の相対速度から計算 B⇔C一般相対論でシュバルツシルト計量から計算 C⇔D特殊相対論ですれ違い様の相対速度から計算
という感じです.
もし,動径方向への自由落下運動で重力を打ち消す場合,その観測系においては, もはや静的な重力場ではなくなるので,動径方向における時間のテンポのズレは, シュバルツシルト計量では計算できないと思います. ただし,動径方向へ自由落下する物体同士であっても,時刻を定めればその瞬間 の固有時間比は,やはり,上記のような三段論法で算出可能だと思います.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/04(Tue) 12:11)
「宇宙ステーション系の動径方向における時間のテンポのズレ」
永久重力場の効果:(dτ/dt)^2=[1-(2GM/c^2)/r]/[1-(2GM/c^2)/R] 回転系の効果:(dτ/dt)^2=[1-(4π^2/c^2)*(r'^2/T^2)]/[1-(4π^2/c^2)*(R'^2/T^2)]
G:重力定数 M:地球の質量 T:宇宙ステーションの公転周期 R:シュバルツシルト時空での宇宙ステーション軌道の換算円周値 R':ミンコフスキー時空での宇宙ステーション軌道の換算円周値 c:真空の光速
r:シュバルツシルト時空での換算円周 r':ミンコフスキー時空での換算円周
単純に線形結合してもいいのかどうか・・・. 問題はr とr' との関係がどうなのかだと思うのですが,よく解りません・・・. しかし,宇宙ステーション系で乗組員の位置(観測点)において,dτ/dt の 動径方向の変化率が0になるのは,直観で予想できそうです.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/04(Tue) 12:44)
なんとなくさん,ミュフ猫さん,ありがとうございます. 私の疑問の本質を理解していただきうれしく思います.
ミュフ猫さん,かなり本質に迫る議論の端緒を提供していただきました.
(1) ひとまず自転は無視して簡略化したいと思います.
(2) 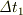 を特殊相対論の範囲で計算することは,近似として許されるのではないかと考えます.
を特殊相対論の範囲で計算することは,近似として許されるのではないかと考えます.
上を承認されれば,問題は
>宇宙ステーション系の動径方向における時間のテンポのズレは,近似的にシュバ ルツシルト計量に従う
の真偽に集約されますね.なるほど,宇宙ステーション系はシュバルツシルト時空に接する局所慣性系ということになるわけでしょうか? そして,その固有時は無限遠時間に対して換算半径に依存して遅れるという理解でいいのかな?
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/04(Tue) 13:27)
Yokkunさん
>宇宙ステーション系はシュバルツシルト時空に接する局所慣性系ということに >なるわけでしょうか?
乗組員の周辺(観測点近傍)では,局所慣性系と言えるのではなでしょうか?
>その固有時は無限遠時間に対して換算半径に依存して遅れるという理解で >いいのかな?
すみません.「近似的にシュバルツシルト計量に従う」とは,
「赤道上の地表から宇宙ステーション軌道までの狭い換算円周値の範囲では」
という条件つきです.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/04(Tue) 21:22)
結局のところ,おおかたのサイトで紹介されている
- 特殊相対論的効果=地上とステーションの相対速度による
- 一般相対論的効果=地上とステーション位置の重力ポテンシャルの差による
の2つが大半を占めるという理解でよいのでしょうね.
私は,ステーションの無重量状態は即重力ポテンシャルゼロの慣性系(シュバルツシルト時空の無限遠に相当)であると早合点したのでした.等価原理の「正しい」間違え方をしたようです.
わかったつもりでも,まだまだ理解の浅いことを思い知らされるこのごろです.
>単純に線形結合してもいいのかどうか・・・. それぞれの要因が独立であるならば,効果は積として記述され,一次近似をとるなら,和になるということでよいのではないでしょうか?今回も迷ったようにそれぞれの「独立性」の判定にいつも迷いが生じます.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/05(Wed) 09:34)
うわ〜!なんか,また,大ボケかましたかも・・・. 調べたら,宇宙ステーション軌道って高度約460キロですね. 赤道半径が約6380キロだから,船内の万有引力は地表上の約0.87倍. どう考えても,「近似的にシュバルツシルト計量に従う」とは言えない.w 静止衛星軌道のレベルだと勘違いしていました.
すみません・・・.m(_ _)m
そう言えば,宇宙ステーションからの映像は,地球が滅茶苦茶デカい. すぐに,おかしいと気づくべきですね・・・.(T_T)
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 14:36)
解答がながすぎてみなさんの方の回答は見ていませんが,僕の回答も聞いてくれるとうれしいです.(同じことを言っているのかもしれないけど)
>他のQ&Aサイトの疑問に対して,知っているつもりで計算しても,全く自信がもてません. 地上の時計の進みをとするとき,速さで運動する若田さんの腕時計の進みは,
まず,疑問なのが,この若田さんって人はどういう状況下にあるんでしょうか? 地球から遠く離れた無重力空間で等速直線運動をしているという考えでいいですか?
だとすると,この式はおかしいと思います.
>地上の時計の進みを  とするとき,速さ
とするとき,速さ  で運動する若打さんの腕時計の進みは
で運動する若打さんの腕時計の進みは
ですが,これはただ単にシュバルツシルド座標における固有時の間隔の関係式でいいのではないでしょうか?そして,速さを考慮に入れるなら,その若田さんのいる「点」の固有時の間隔 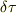 と,若田さんの固有時の間隔
と,若田さんの固有時の間隔 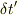 の関係式を特殊相対論で求めればいと思いますが,特殊相対論はあくまで相対的な時間の遅れ(どちらを基準にするかにより決まってくる)なので,そこまで考える必要はない気がします.つまり,地上と若田さんのいる「点」との固有時間の間隔をシュバルツシルド座標で求めればいいと思います.(ただし地球は自転していないものとする)
そうすれば,どちらの時間のテンポが遅いか一目瞭然だと思います.それは明らかに地上であるということが理解できるはずです.
の関係式を特殊相対論で求めればいと思いますが,特殊相対論はあくまで相対的な時間の遅れ(どちらを基準にするかにより決まってくる)なので,そこまで考える必要はない気がします.つまり,地上と若田さんのいる「点」との固有時間の間隔をシュバルツシルド座標で求めればいいと思います.(ただし地球は自転していないものとする)
そうすれば,どちらの時間のテンポが遅いか一目瞭然だと思います.それは明らかに地上であるということが理解できるはずです.
ただし,厳密には地上は大気中にあるため,物質中だと思うので,シュバルツシルド座標に適合しない可能性があります.(近似的なら大丈夫かな?)
>さて,長くなりましたが,若田さんの過ごした時間は地上に比べて実際進んだのか遅れたのかどっちなのでしょう
相対速度を考慮に入れるなら,若田さんを基準にするか,地上を基準にするかによって結果が異なってくると思いますが,そういった座標系の取り方に応じた見かけ上の時間の遅れではなく,「本質的な時間の遅れ」を問題とするなら,地上の方が時間の進みのテンポが遅いと思います.
ただし,地上から出発して地上に帰ってくる場合,加速運動をするので,その場合にも本質的な時間の遅れが問題になると思います.が,問題文を見る限りそのような初期条件はないようなので,無視しました.
もうすでにこのことを誰かが言っていたらごめんなさい.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/05(Wed) 17:13)
トビラ..さん,考察に参加していただきありがとうございます.
>地上から出発して地上に帰ってくる場合,加速運動をするので,その場合にも本質的な時間の遅れが問題になると思います.
これがまさに特殊相対論的な時間の遅れが「絶対化」する原因だと思います. もちろん,若田さんが行く前と帰ってきた後で時刻合わせをしようというのが疑問の主題(はっきりしないでごめんなさい)ですから,これを計算に入れないわけにはいかないのです.言い換えると,ステーションに行って帰ってくるまでの若田さんの固有時と地上の固有時の差を概算しようというわけです.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/05(Wed) 19:45)
トビラ..さん,こんばんは.
「双子のパラドックス」では,方向転換した方が加速度運動分だけ時間が遅れます. 今回の場合,若田さんが地上に戻っても,地上の観測者が宇宙ステーションまで 連れ戻しに行っても,若田さんの方の時計が遅れると思うのですが・・・. というのは,地上を基準にした相対速度による若田さんの時計のテンポのズレは, 若田さんが周回軌道上のどこにいても同じですが,若田さんを基準にした地上の それは,若田さんの位置に依存して周期的に変動すると思うからです. 常に同じであれば,単純に滞在時間を乗じればトータルの遅れが計算できます. 変動するならば,滞在時間で積分しなければトータルの遅れが判りません. なぜ,そうなるのか説明が難しいです. 空間二次元+時間一次元のミンコフスキー時空図で,等速円運動する観測者の 同時刻平面の移り変わりを想像して得た結論です.
また,やらかすのかな・・・?(^^;)
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 21:48)
Yokkunさんへ 回答ありがとうございます.
>これを計算に入れないわけにはいかないのです.
地上から出発して地上に戻っていくるという条件にないのであれば,それを計算に入れる必要はないと思います.例えば,ある時刻に地球か若田さんの乗った宇宙船に光を送ったとします.この光は地上で一秒ごとに光を放つものとします.そうすると,若田さんが観測する光の間隔は伸び,1秒ではなくなります.これを合計すると本質的な時間のトータルの遅れが計算できます. なので,本質的な時間の遅れを計算するのに必ずしも地球から出発して地球に帰ってくるという条件は必要ないです. しかし,そのような条件があるということなので,その場合はYokkunさんの言うとおり,その加速運動が本質的な時間の遅れの原因となるとおもいます.
ミュフ猫さんへ お返事ありがとうございます.
>「双子のパラドックス」では,方向転換した方が加速度運動分だけ時間が遅れます. 今回の場合,若田さんが地上に戻っても,地上の観測者が宇宙ステーションまで 連れ戻しに行っても,若田さんの方の時計が遅れると思うのですが・・・. というのは,地上を基準にした相対速度による若田さんの時計のテンポのズレは, 若田さんが周回軌道上のどこにいても同じですが,若田さんを基準にした地上の それは,若田さんの位置に依存して周期的に変動すると思うからです.
僕の回答を見てもらえたらわかるように,僕は初めの問題文に対してのみ答えたつもりです.なので,宇宙ステーションとか地球を周回しているとか条件にはめてませんでした.・・・?・・・!?・・・!!!ってかもしかして若田さんて宇宙飛行士のあの人ですか!?今気づきました.(いままで,わか「だ」さんって読んでた.鈍くてごめん)なんで,この名字の人が主人公なのだろうと疑問に思ってましたがそういう意味でしたか.
(つまり,地球の周りを円運動していたんですね)
だとすると,この場合,簡単のため条件として,あらかじめ若田さんは周回軌道上(?)にいるとして,地球は簡単のため回転していないものとして(Kerr解を用いれば容易に拡張できるが少し面倒なのでほおっておく)また,若田さんと地球との相対角速度を  とし,地上と地球の中心の点との距離を
とし,地上と地球の中心の点との距離を  とし,若田さんのと地球の中心との距離を
とし,若田さんのと地球の中心との距離を 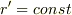 と地球原点との距離を一定に保っているものとします.また,地球から出発したとか地球に生還したとかは簡単のため問題としないことにします.(問題にすることもできるがそれなりの宇宙船の運動方程式が新たに必要なので,それを考えるの面倒なのでやめておきます.)
シュバルツシルド座標系において
と地球原点との距離を一定に保っているものとします.また,地球から出発したとか地球に生還したとかは簡単のため問題としないことにします.(問題にすることもできるがそれなりの宇宙船の運動方程式が新たに必要なので,それを考えるの面倒なのでやめておきます.)
シュバルツシルド座標系において 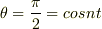 とし(つまり,簡単化のため大円周のみを対象とする,),
とし(つまり,簡単化のため大円周のみを対象とする,), 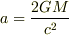 をシュバルツシルド半径とすると,
をシュバルツシルド半径とすると,
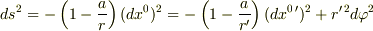 となり,ここで,
となり,ここで, 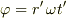 なので,簡単な式変形の結果(
なので,簡単な式変形の結果( 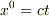 として)
として)
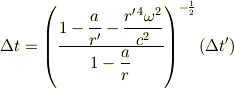
となりますよね?ここで, 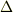 とは時間の間隔という意味です.また,
とは時間の間隔という意味です.また,  は地上の固有時間,
は地上の固有時間, 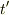 は軌道上の宇宙船の固有時間です.これが,それぞれの固有時間の間隔の関係式ではないでしょうか?(わかると思いますが,速度
は軌道上の宇宙船の固有時間です.これが,それぞれの固有時間の間隔の関係式ではないでしょうか?(わかると思いますが,速度  は相対角速度
は相対角速度  に含まれています.)
また,本来Schwarzschild座標は真空中しか適応できませんので,簡単化のため,地球の大気は無視しました.(密度が薄いから近似的に大丈夫かな?)
僕はこの式で問題ないと自負しています.
(もっと詳細な条件を与えられれば,もっと詳細な方程式に拡張することができます.例えば,地上に宇宙船が離陸着陸する場合,Schwarzschild座標において
に含まれています.)
また,本来Schwarzschild座標は真空中しか適応できませんので,簡単化のため,地球の大気は無視しました.(密度が薄いから近似的に大丈夫かな?)
僕はこの式で問題ないと自負しています.
(もっと詳細な条件を与えられれば,もっと詳細な方程式に拡張することができます.例えば,地上に宇宙船が離陸着陸する場合,Schwarzschild座標において 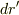 の項も考慮に入れればいいが,その場合,
の項も考慮に入れればいいが,その場合, 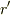 と
と 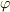 の関係式,つまり,宇宙船の運動方程式を独立に必要とする.また,宇宙船が大円周上になくとも,
の関係式,つまり,宇宙船の運動方程式を独立に必要とする.また,宇宙船が大円周上になくとも, 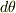 などの項も考慮に入れればよい.また,地球の観測者が地上を移動している場合にも初めの式の左辺(
などの項も考慮に入れればよい.また,地球の観測者が地上を移動している場合にも初めの式の左辺( 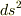 の右の式)の
の右の式)の 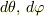 をゼロとしなければよい.その代わりその観測者の
をゼロとしなければよい.その代わりその観測者の 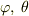 間の方程式,つまりは観測者の運動方程式が別途必要となる.これらがそろえば,計算は複雑にこそなるが上述の計算の延長上にあるはずである.)
間の方程式,つまりは観測者の運動方程式が別途必要となる.これらがそろえば,計算は複雑にこそなるが上述の計算の延長上にあるはずである.)
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/05(Wed) 23:00)
トビラ..さん,なるほどそういうことになるのですね.
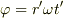 は,
は,
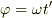 でよいのでしょうね?
すると,
でよいのでしょうね?
すると,
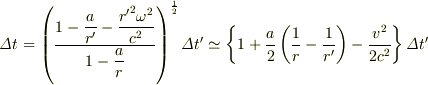 となるのかな?
#Δt'修正しました.
となるのかな?
#Δt'修正しました.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 23:05)
>また,やらかすのかな・・・?(^^;)
あの話でしたら,未だに僕は間違っていなかったと思っていますし,あのトピの最後から2番目のレス(?)を見てください.ちゃんと補足しています.多分あの補足でみんなに通じると自負しています.
ただ,たけしのテレビタックルならぬ,物理のカギ尻尾タックルにならぬよう気をつけます.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 23:07)
>でよいのでしょうね?
しまった間違った.それさっき式を修正しているとき  が足りない!!と思って
が足りない!!と思って  を付け足したんです.修正するんじゃなかった.
を付け足したんです.修正するんじゃなかった.
 をつけたら速度ですね.ガーン
(言い訳は僕の十八番です.グヘヘ)
をつけたら速度ですね.ガーン
(言い訳は僕の十八番です.グヘヘ)
Re: 若田さんが過ごした時間
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 23:28)
こんな機会がなかったらGPSの補正のことについて具体的に式を考えませんでした.なんか得した気分です.なんかありがとうございます.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/05(Wed) 23:32)
あ,あと,Yokkunさんの書いた近似の式,右辺に 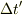 が抜けてるよね?
が抜けてるよね?
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/05(Wed) 23:38)
あ,先をこされてしまった.
その通りです.つけときますねー. この結果はいわゆる「特殊相対論的な効果」を含んでいるということになるわけですよね!これでいわゆる「特殊相対論的な効果」と「一般相対論的な効果」とをひとつの計量から導出できるということがわかってすっきりしました.トビラ..さん,ありがとうございました.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/05(Wed) 23:44)
トビラ..さん,ご返事ありがとうございます.
(dt[station])^2 = (1-a/r')・(dt)^2 - (r'/c)^2・(dφ)^2,ω=dφ/dt[shell]
(dt[shell])^2 = (1-a/r')・(dt)^2
(dt[earth])^2 = (1-a/r)・(dt)^2
よって,
(dt[station]/dt[earth])^2 = {(1-a/r')/(1-a/r)}・{1-(r'ω/c)^2}
となるような気がします.ここで,
t[earth]:地上の固有時間 t[shell]:宇宙ステーション軌道上に静止する観測者の固有時間 t[station]:宇宙ステーションの固有時間
です.そして,
t:遠方時間(無限遠で静止する観測者の固有時間)
です. シュバルツシルト計量方程式の変数tは,常に「遠方時間」になるかと思うのですが・・・.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/05(Wed) 23:49)
トビラ..さん.
>あの話でしたら,未だに僕は間違っていなかったと思っていますし, >あのトピの最後から2番目のレス(?)を見てください. >ちゃんと補足しています.多分あの補足でみんなに通じると自負しています.
誤解です! 私自身に対して「また,やらかしたか?」と言っているのです!! 大ボケしまくりですので.w
Re: 若田さんが過ごした時間
yama さんのレス (2009/08/06(Thu) 00:11)
「シュバルツシルト計量方程式の変数tは,常に「遠方時間」になる」というミュフ猫さんの考えが正しいと思います. つまりωは無限遠から観測した角速度ですね. 地球の場合はこの違いはほとんど問題にならないでしょうが,ブラックホール近傍の運動では違いが無視できなくなるでしょうね.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/06(Thu) 00:34)
yamaさん,こんばんは.
>つまりωは無限遠から観測した角速度ですね.
いえいえ,
ω=dφ/dt[shell]
ですから,宇宙ステーション軌道上に静止する観測者が,目の前を通過する瞬間に 感じる宇宙ステーションの速度を,軌道までの換算円周で割ったものです. (ややこしい.w)
上のサイトの「物体の速度:v」の定義に合わせてみました.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 00:54)
ああああああああああぁぁぁぁぁぁぁぁ!!!!そうでした,思いっきり座標時間を固有時間といってました.間違えましたスミマセン. 今度,1リットルの水道水おごります!!!許してくだはい
Re: 若田さんが過ごした時間
yama さんのレス (2009/08/06(Thu) 01:20)
確かにミュフ猫さんの式では軌道上の静止観測者が観測した角速度になりますね. 式をよく見るとトビラさんとミュフ猫さんでは,同じωでも意味が違っているようで,トビラさんの式では,ωは無限遠から観測した角速度になると思います.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 06:06)
■■■修正中■■■
ミュフ猫さんの式の間違えを見つけました.エッヘン
ミュフ猫さんは地上の座標時間の間隔と,宇宙船の座標時間の間隔を等しくしていますが,その数学的根拠が示されていません.事実,僕が計算するとこの2つの座標時間の間隔は等しくなかったです.その計算は後で紹介してもう少しこのことに触れていましょう.
思考実験からのアプローチでもそのようになることが理解できます.なぜなら,座標時間において  の間隔で地上から宇宙船に光を送ったとしても,宇宙船で受け取るその間隔は
の間隔で地上から宇宙船に光を送ったとしても,宇宙船で受け取るその間隔は  でなくなることは容易にわかるからです.絵にして書いてみるとよくわかる.
例えば,光の赤方偏移の問題を解く場合,このように地上の座標時間と星との座標時間が等しいことをそのように信号の座標時間の間隔により証明します.
では,具体的にこの2つの座標時間の関係式を導出していきましょう.
まず,地上の座標時間の間隔
でなくなることは容易にわかるからです.絵にして書いてみるとよくわかる.
例えば,光の赤方偏移の問題を解く場合,このように地上の座標時間と星との座標時間が等しいことをそのように信号の座標時間の間隔により証明します.
では,具体的にこの2つの座標時間の関係式を導出していきましょう.
まず,地上の座標時間の間隔  とその「真上」の「静止している」宇宙船との座標時間の間隔は,今述べた光の赤方偏移の計算で既に証明されているのはご存じだと思います.よって,この2つの座標時間は等しいことは証明されているので,言い換えれば,「静止している」宇宙船と,「地球の周りを円運動している」宇宙船の座標時間の間隔の関係式を求めればいいわけです.
ここで,静止している宇宙船の座標時間(地上の座標時間)を
とその「真上」の「静止している」宇宙船との座標時間の間隔は,今述べた光の赤方偏移の計算で既に証明されているのはご存じだと思います.よって,この2つの座標時間は等しいことは証明されているので,言い換えれば,「静止している」宇宙船と,「地球の周りを円運動している」宇宙船の座標時間の間隔の関係式を求めればいいわけです.
ここで,静止している宇宙船の座標時間(地上の座標時間)を  ,動いている宇宙船の座標時間を
,動いている宇宙船の座標時間を 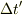 とします.
基本となる関係式はシュバルツシルド座標より
とします.
基本となる関係式はシュバルツシルド座標より
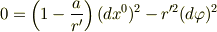
となるはずです.これを第1式と呼ぶことにします.(赤方偏移同様に光の間隔つまり,情報伝達の速度の間隔を採用.) 第1式より,簡単な式変形の結果
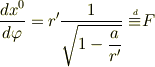
となります.ここで,面倒なので,  と定義しました.
静止宇宙船(静止している宇宙船)の時計で時刻
と定義しました.
静止宇宙船(静止している宇宙船)の時計で時刻  のとき,動宇宙船(大円周上を動いている宇宙船)に向かって信号を送りました.その信号を動宇宙船が受け取った時刻(動宇宙船で測った時刻)を
のとき,動宇宙船(大円周上を動いている宇宙船)に向かって信号を送りました.その信号を動宇宙船が受け取った時刻(動宇宙船で測った時刻)を 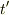 とします.また,静止宇宙船がその
とします.また,静止宇宙船がその 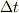 後にまた,信号を送ったとします(もちろんこの
後にまた,信号を送ったとします(もちろんこの  はあくまで静止宇宙船で測った時刻).
その2つ目の信号を動宇宙船が受け取った時刻(もちろんこれは動宇宙船で測った時刻)を
はあくまで静止宇宙船で測った時刻).
その2つ目の信号を動宇宙船が受け取った時刻(もちろんこれは動宇宙船で測った時刻)を 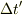 とします.
でいま求めたいのは
とします.
でいま求めたいのは  と
と 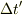 です.
そこで,方程式を立てると
です.
そこで,方程式を立てると
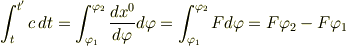
となります.( 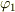 は静止宇宙船の座標(角度),
は静止宇宙船の座標(角度), 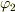 は時刻
は時刻 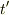 の動宇宙船の
の動宇宙船の 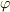 の座標(角度),また,
の座標(角度),また, 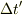 の間に変化した宇宙船の座標を
の間に変化した宇宙船の座標を 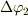 とする.)
また,もう一つ式が立てられ,すなわち
とする.)
また,もう一つ式が立てられ,すなわち
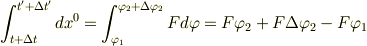
となります.したがって,この2つの式をつなげると
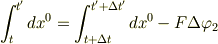
となり,計算を進めると,単純な積分の結果(また, 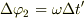 なので,)
なので,)
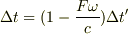 となります.
後は
となります.
後は  を代入すればそれが,静止宇宙船の座標時間の間隔
を代入すればそれが,静止宇宙船の座標時間の間隔  すなわち,地上の座標時間の間隔
すなわち,地上の座標時間の間隔  と動宇宙船の座標時間の間隔
と動宇宙船の座標時間の間隔 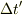 の関係式が得られます.(事実この式の角速度
の関係式が得られます.(事実この式の角速度 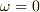 のときは動宇宙船と静止宇宙船の座標時間が一致する)
この関係式を用いて,ミュフ猫さんの式に代入してもう少し厳密に求めるべきだと思います.
つまり,座標時間の関係式は
のときは動宇宙船と静止宇宙船の座標時間が一致する)
この関係式を用いて,ミュフ猫さんの式に代入してもう少し厳密に求めるべきだと思います.
つまり,座標時間の関係式は
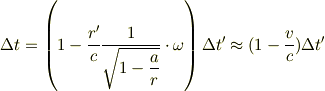
速度  が
が  だと,予想通り2つの座標時の間隔が一致する.
だと,予想通り2つの座標時の間隔が一致する.
Re: 若田さんが過ごした時間
yama さんのレス (2009/08/06(Thu) 07:43)
>ミュフ猫さんは地上の座標時間の間隔と,宇宙船の座標時間の間隔を等しくしていますが
ミュフ猫さんの式ではrとr'の違いがあるので,等しくはなっていないと思いますが・・・.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 07:56)
等しくなっていないのは座標時間ではなく固有時間だと思います.
もし,座標時間が別々のものだとしたら座標時間をそれぞれ,  と
と 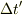 として区別をはっきりするべきです.そして,その座標時間の関係式も必要になります.
しかし,ミュフ猫さんはそうしていないので,最終的な式を求めるとき,この2つの座標時間の間隔を同じものと考え,方程式を解いているように見えますよ?
として区別をはっきりするべきです.そして,その座標時間の関係式も必要になります.
しかし,ミュフ猫さんはそうしていないので,最終的な式を求めるとき,この2つの座標時間の間隔を同じものと考え,方程式を解いているように見えますよ?
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/06(Thu) 09:19)
私が寝苦しい夜をベッドで過ごしている間にどんでん返しがあったようで・・・. またこれから小旅行に入るので整理させてください.
地上およびステーション内の固有時の進み 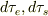 に対して
に対して
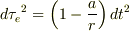
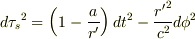 したがって,
したがって,
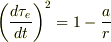
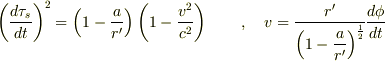 となり,地上に対するステーション内の固有時の進みの比は
となり,地上に対するステーション内の固有時の進みの比は
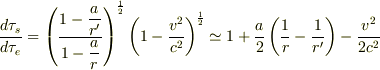
えーと,  の解釈がいまいち・・・.
換算半径
の解釈がいまいち・・・.
換算半径 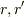 は,上の近似の精度で地球からの測定値に置き換えて問題ないですか?
は,上の近似の精度で地球からの測定値に置き換えて問題ないですか?
一方トビラ..さんの問題意識は,
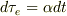
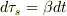 と書けるときに,
と書けるときに,
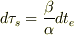 (
( 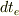 は地上系の時間の進み)
となるといえるのか,ということになりますか?後の議論はまだ読み取れていません.
は地上系の時間の進み)
となるといえるのか,ということになりますか?後の議論はまだ読み取れていません.
Re: 若田さんが過ごした時間
yama さんのレス (2009/08/06(Thu) 10:22)
固有時間の比を求めればよいのであって,座標時間は直接には関係ないように思います. 地上と宇宙船の時計の進み方は座標系のとりかたによって変わるわけではないので,それぞれの固有時間で比較すべきでしょう.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/06(Thu) 14:09)
トビラ..さん.
>最終的な式を求めるとき,この2つの座標時間の間隔を同じものと考え, >方程式を解いているように見えますよ?
ですから,シュバルツシルト計量は,無限遠に静止する遠方観測者が主張する 時空間のパラメーターです. つまり,座標時間は常に「遠方時間」で各固有時間は須らく,一旦,「遠方時間」 を基準に比較されます. そして,遠方観測者と同時刻空間を共有する観測者達だけが,自分を基準にした 固有時間比を,シュバルツシルト計量方程式から知り得るのだと思います. (これが「三段論法」です.) 具体例で,
t[earth]:地上の固有時間 t[shell]:宇宙ステーション軌道上に静止する観測者の固有時間 t[station]:宇宙ステーションの固有時間 t:遠方時間(無限遠で静止する観測者の固有時間)
γ[ear→she]:地上の観測者から見た宇宙ステーション軌道上に静止する観測者との固有時間比 γ[she→ear]:宇宙ステーション軌道上に静止する観測者から見た地上の観測者との固有時間比 γ[she→sta]:宇宙ステーション軌道上に静止する観測者から見た宇宙ステーション内の観測者との固有時間比 γ[sta→she]:宇宙ステーション内の観測者から見た宇宙ステーション軌道上に静止する観測者との固有時間比 γ[ear→sta]:地上の観測者から見た宇宙ステーション内の観測者との固有時間比 γ[sta→ear]:宇宙ステーション内の観測者から見た地上の観測者との固有時間比
とすると,
γ[ear→she] = dt[shell]/dt[earth] = {(1-a/r')/(1-a/r)}^(1/2) γ[she→ear] = dt[earth]/dt[shell] = {(1-a/r)/(1-a/r')}^(1/2)
γ[she→sta] = dt[station]/dt[shell] = {1-(r'ω/c)^2}^(1/2) γ[sta→she] = dt[shell]/dt[station]≧{1-(r'ω/c)^2}^(1/2) ,(時間周期関数で,等号はすれ違う瞬間に成立)
γ[ear→sta] = dt[station]/dt[earth] = [{(1-a/r')/(1-a/r)}・{1-(r'ω/c)^2}]^(1/2) γ[sta→ear] = dt[earth]/dt[station] > [{(1-a/r)/(1-a/r')}・{1-(r'ω/c)^2}]^(1/2) ,(時間周期関数)
で,宇宙ステーション基準の固有時間比は,「三段論法」が成り立ちません. その理由は宇宙ステーション内の観測者のみが,その他の三人の観測者に対して, 同時刻空間を共有しないからです.
またまた,やらかしたか・・・?(^^;)
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 18:11)
同時刻がなりたたないので,その座標時間との関係式を求めようとしているんですよ? なんかもやもやかんはあるんですが,なんか納得いかないです.
座標時間 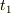 から,
から, 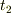 の間の間隔を
の間の間隔を  とすると,この間に地上から放たれた光(信号)が,座標時間の
とすると,この間に地上から放たれた光(信号)が,座標時間の 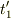 に初めの信号が宇宙船に届き,座標時間の
に初めの信号が宇宙船に届き,座標時間の 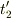 に最後の信号が宇宙船に届いたとします.この間
に最後の信号が宇宙船に届いたとします.この間 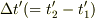 .つまり,地上ではかった,座標時間の間隔
.つまり,地上ではかった,座標時間の間隔  に対応するのが,宇宙船では座標時間の間隔は
に対応するのが,宇宙船では座標時間の間隔は 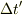 と変形しているはずです.
地上での固有時と座標時の関係式は
と変形しているはずです.
地上での固有時と座標時の関係式は
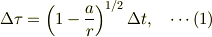
宇宙船での固有時と座標時との関係式は
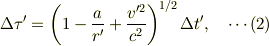
ただしここで, 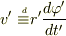 と定義しました.
そうすると,この式を見てわかるようにこの2つの式をつなげるためには
と定義しました.
そうすると,この式を見てわかるようにこの2つの式をつなげるためには  と
と 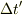 間の関係式が必要だと思います.赤方偏移の問題の場合は
間の関係式が必要だと思います.赤方偏移の問題の場合は 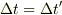 と証明されていますが,今回その証明を吟味していないように思います.
と証明されていますが,今回その証明を吟味していないように思います.
ここで,楽しいウサギちゃんの話をしましょう.(僕が言いたいのはつまりこういうことです.)
座標時間を測ることのできる時計をもったウサギがいたとします.そのウサギが地上にいて,その便利な時計の時刻 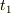 のときに宇宙船に向かって光を放ったとします.その後,ウサギがその時計の時刻
のときに宇宙船に向かって光を放ったとします.その後,ウサギがその時計の時刻 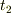 のときに宇宙船に向かってまた光を放ちます.したがって,その間は
のときに宇宙船に向かってまた光を放ちます.したがって,その間は 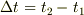 です.さて,この後ウサギは秘密の抜け道を通り宇宙船にワープしたとします.そして,この宇宙船でさっき地上から放った光が届くのを待ちます.すると,ウサギの時計で時刻
です.さて,この後ウサギは秘密の抜け道を通り宇宙船にワープしたとします.そして,この宇宙船でさっき地上から放った光が届くのを待ちます.すると,ウサギの時計で時刻 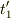 のとき始めの光が届き,時刻
のとき始めの光が届き,時刻 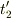 のとき2番目に放った光が届いたとします.その間隔は
のとき2番目に放った光が届いたとします.その間隔は 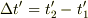 となります.これを数式にして解けば,座標時間の間隔の関係式がもとまるのではないでしょうか?
例えば,地上の固有時間の間隔
となります.これを数式にして解けば,座標時間の間隔の関係式がもとまるのではないでしょうか?
例えば,地上の固有時間の間隔 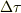 は,地上の座標時間の間隔
は,地上の座標時間の間隔  によって表現できます(上式の(1)式).
また,宇宙船での固有時間の間隔
によって表現できます(上式の(1)式).
また,宇宙船での固有時間の間隔 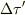 は,その地上の座標時間の間隔に対応する,宇宙船の座標時間の間隔
は,その地上の座標時間の間隔に対応する,宇宙船の座標時間の間隔 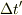 により決まります(定式の(2)式).
なので,この2つの座標時間の間隔の関係式をもとめて,代入する必要があると思うんですが・・・・
により決まります(定式の(2)式).
なので,この2つの座標時間の間隔の関係式をもとめて,代入する必要があると思うんですが・・・・
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 18:26)
ミュフ猫さんや,Yokkunさんの言っていることは理解しているつもりですよ.こういうことですよね?
 という間隔を基準にして,地上の固有時間と,宇宙船の固有時間をあらわし,その式から,
という間隔を基準にして,地上の固有時間と,宇宙船の固有時間をあらわし,その式から,  を消せばよい.
を消せばよい.
僕もこれはこれで正しい気がしますが,なぜか上述の僕の考えも間違っている気がしないんです.ゆえに自分のなかでもやもやかんがあるというか・・・
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 19:08)
どの座標時間の間隔を基準にするかに寄るんですかね? 光の赤方偏移の場合,光を放つ座標時間の間隔と光を受け取る座標時間の間隔が問題となりますが,今回の場合,光(情報の伝達)の問題ではないので,座標時間同士の関係式は任意に選ぶことができるってことなのでしょうか?
つまり,僕の計算は情報の送信の(時間の)問題で,ミュフ猫さんが扱っているのは本質的な時間の問題?
かな?よくわかんない.
あと,三段論法のレスで,不等式が出てきてましたけど,なんで不等式になっているのかよくわからなかったです.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/06(Thu) 19:21)
トビラ..さん,ご返事ありがとうございます.
赤方偏移について,空間を進む光波の振動数が,伝播中に変化するわけではなく, 送り手,受けての立場(観測系)によって,変化したように感じると言うことかと 思います. ですから,送り手,受け手が共に静止しているときには,当然,
?t = ?t'
となると思います.静的な重力場では光波の到達所要時間が,発光時刻に依存 しませんから. よって,宇宙ステーションが地上の観測者の真上を通過する瞬間に,地上からの 光波が届くタイミングで実験したなら,やはり,
?t = ?t'
だと思いますが・・・.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/06(Thu) 19:26)
トビラ..さん,ご返事ありがとうございます.
>三段論法のレスで,不等式が出てきてましたけど,なんで不等式になっている >のかよくわからなかったです.
なぜ,そうなるのか説明が難しいです. 空間二次元+時間一次元のミンコフスキー時空図で,等速円運動する観測者の 同時刻平面の移り変わりを想像して得た結論です.
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/06(Thu) 20:03)
>光波が届くタイミングで実験したなら,やはり,
なるほど,  を宇宙船の地球を回る周期だと考えれば,いいわけですね.少し考えます.
を宇宙船の地球を回る周期だと考えれば,いいわけですね.少し考えます.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/06(Thu) 23:05)
重力赤方偏移の議論のときに,シュバルツシルト時空の任意の静止した2点間での光のやりとりにおいて,光を発した時間と受け取った時間は座標時(無限遠時間)において等しいことが証明されたのでしたね.
そこで,BからAに届いた光信号の継続時間がまさにBの時間をAから「観測した」ものであるということを認めるなら,ただちにAから見たBの時間の伸び縮みは相互の固有時の比で決まるといえそうです.
今までと逆の展開をしてみましょう.
A(地球半径),B(ステーション半径)の2箇所に各固有時において等しい光パルスを出す基準発信機をおきます.ただし,ここでは簡単のため自転も公転も考慮しません.シュバルツシルト計量が直接教えることは,パルスの発信時間 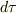 が,
が,
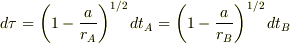
となることです.ただし, 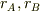 はA,Bの換算半径,
はA,Bの換算半径, 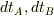 は座標時間によるA,Bから出たパルス長すなわち無限遠から見たパルスの継続時間です.
は座標時間によるA,Bから出たパルス長すなわち無限遠から見たパルスの継続時間です.
さて,Bから出たパルスをAが受信する時間は,無限遠時間において 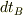 のままです.するとAが観測するBのパルス長は
のままです.するとAが観測するBのパルス長は
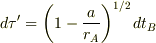
であるはずです.
しかるに,Aの手元の発信機が出すパルス長は 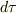 に他なりませんから,Aで観測されるBのパルス長は手元の発信機が出すパルス長に対して
に他なりませんから,Aで観測されるBのパルス長は手元の発信機が出すパルス長に対して
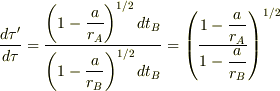
の比を持つことになりますよね?
Re: 若田さんが過ごした時間
トビラ.. さんのレス (2009/08/07(Fri) 02:00)
ごめんなさい今あるバイトで久々に夜勤なので,携帯でしか見れないです. 返事当分遅くなるとおもいます.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/08(Sat) 09:55)
ひとまず,計算結果を紹介しておきます.
地上時間と宇宙ステーション時間の比は, 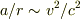 程度の微小量について1次の近似をとって,
程度の微小量について1次の近似をとって,
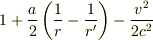
すると,地上時間 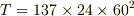 [s]に対する宇宙ステーション時間の差は概算で,
[s]に対する宇宙ステーション時間の差は概算で,
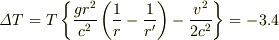 [msec.]
[msec.]
となりました.うちわけは,
- 特殊相対論的効果-3.9msec.
- 一般相対論的効果+0.5msec.
といったところ. ちなみに,ニュートン力学において
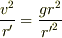
なので,
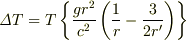
となり, 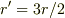 のときに(1)(2)が相殺することは,ミュフ猫さんにご紹介いただいた
のときに(1)(2)が相殺することは,ミュフ猫さんにご紹介いただいた
にあるとおりです.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/09(Sun) 22:00)
Yokkunさん.
>ただし,ここでは簡単のため自転も公転も考慮しません.
地球の「自転」と,宇宙ステーションの「公転」ということですね? なら,その通りだと思います.やっと,理解しました. この場合,Bで観測されるAのパルス長は手元の発信機が出すパルス長に対して,
dτ/dτ'
の比をもつことも言えると思います.
>うちわけは, > >(1) 特殊相対論的効果-3.9msec. >(2) 一般相対論的効果+0.5msec. > >といったところ.
なるほど.やっぱり,特殊の効果が大きいですね・・・.
Re: 若田さんが過ごした時間
Yokkun さんのレス (2009/08/09(Sun) 22:27)
>地球の「自転」と,宇宙ステーションの「公転」ということですね? なら,その通りだと思います.やっと,理解しました.
ちょっと単純化しすぎましたか? トビラ..さんの疑問に応えるのに十分かと思ったのですが,すでに
>赤方偏移の問題の場合はΔt=Δt'と証明されていますが,
と書かれていますね.蛇足になったようです.
>なるほど.やっぱり,特殊の効果が大きいですね・・・.
静止衛星では一般相対論的効果が大きくなるようですが,GPS衛星と違って補正とかの必要はないようにも思えます.実際の観測値とかあると面白いんですけどね.
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/09(Sun) 22:53)
>静止衛星では一般相対論的効果が大きくなるようですが,GPS衛星と違って >補正とかの必要はないようにも思えます.
高度が4万キロを超えますから,おそらく,そうでしょうね. ここまでくれば,「近似的にシュバルツシルト計量に従う」と言えそうな.w
Re: 若田さんが過ごした時間
ミュフ猫 さんのレス (2009/08/10(Mon) 09:34)
すみません.m(_ _)m No:25142を修正しました.
位置の異なる二点間では,瞬間的に同時刻を共有するという理由だけで, シュバルツシルト計量を利用して,固有時間比を導出するのは難しそうです. 少なくとも,回転系の効果がある分,単純に「三段論法」で導出した値より 大きくなりそうなので.
やっぱり,やらかしたか・・・.(T_T)