圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
重厚にして実務型 さんの書込 (2009/08/03(Mon) 12:30)
はじめまして,今高校三年なのですが,古い参考書で解答なしの問題を解いておりまして,ひとつわからないところがあり,休み中聞く人がいないのでこの掲示板にて質問させていただきました.
理想気体の簡単な状態変化の問題です.
問題:理想気体の状態方程式PV=RTに従うC[p]/C[v]=γの気体があり,P=kV(ただしkは比例定数)で体積をV[A]からv[B]に変化させる.v[B]=2V[A]として,終状態での気体がする仕事,吸収する熱,内部エネルギーの変化を求めよ.
まず私は変化後の温度を求めました.それは4kT[A]になると思います.そして仕事も簡単で,P-Vグラフ上での台形の面積から3kV[A]^2/2と出ました. 問題は吸収熱と内部エネルギー変化なのですが,ここで手が止まっています.圧力も体積も温度も変化する場合,吸収熱はどのようにして算出するのでしょうか.見たことも無かったので難しく感じています.吸収熱が分かれば内部エネルギーも分かるのですが.
詳しい方教えていただけないでしょうか.
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
Yokkun さんのレス (2009/08/03(Mon) 13:47)
重厚にして実務型さん,こんにちは.私も熱力学は苦手ですが,高校レベルなら何とかなるかも.
まず, 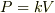 に沿って変化することが与えられていますが,
に沿って変化することが与えられていますが,  は次元のある(単位のある)定数ですから,
は次元のある(単位のある)定数ですから, 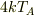 が温度にならないことに気づけるようになると強いです.
が温度にならないことに気づけるようになると強いです.  はいりませんね?
はいりませんね?
この場合,吸収熱は直接計算できないと思います.一方,比熱に関する情報が与えられていますから,内部エネルギー変化が計算できるのです.そこで,吸収熱は熱力学第一法則で逆算すればいいわけです.
内部エネルギーはその意義からして温度のみの関数として表されるはずですね?
次のように考えます.定積変化のとき 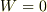 ですから,熱力学第一法則により
ですから,熱力学第一法則により 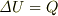 .定積比熱の意味から,
.定積比熱の意味から,
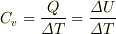 したがって,
したがって,
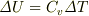 と書けることになります.定積変化のときに限ったのは
と書けることになります.定積変化のときに限ったのは 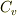 を用いるためだけなので,この関係はどんな変化においても成立する関係なのです.
を用いるためだけなので,この関係はどんな変化においても成立する関係なのです.
ひとまず,これで内部エネルギーの変化を求めてみませんか?
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
重厚にして実務型 さんのレス (2009/08/03(Mon) 23:28)
Yokkunさん,はじめてでしたのに気持のよい回答をしていただいてありがとうございました.非常に丁寧で分かりやすい説明でしたので方針はすんなり理解することができました.ありがとうございます. 最後に一つだけ質問させてください.
温度については私の記述ミスでした.kは不要で4T[A]です. 内部エネルギーについてなのですが,では具体的には U=∫[T[A]→T[B]] C[v] dT ということになりますよね.定積比熱はTの関数なので定数扱いできず,またここから変形が必要ですよね. 定積比熱がTの関数になるのは個体の場合と読んだことがあるのですが,では今回は理想気体なので単純に定数扱いで来て,U=C[v](T[A]-T[B])としていいのでしょうか.あとは仕事と組み合わせて吸収熱を求めればよいということでしょうか.
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
Yokkun さんのレス (2009/08/03(Mon) 23:47)
>今回は理想気体なので単純に定数扱いできて,
単原子分子の場合は特定されて, 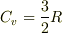 でしたよね?
現実の気体では比熱は温度によって変化しますが,それは特に温度が低い場合には分子間力が無視できなくなって,内部エネルギーの中に分子間力による位置エネルギーが含まれるからです.理想気体は,分子間力を無視した仮想的なモデルなので,これを無視すると温度に依存しない定数として扱うことが許されるのだと思います.
でしたよね?
現実の気体では比熱は温度によって変化しますが,それは特に温度が低い場合には分子間力が無視できなくなって,内部エネルギーの中に分子間力による位置エネルギーが含まれるからです.理想気体は,分子間力を無視した仮想的なモデルなので,これを無視すると温度に依存しない定数として扱うことが許されるのだと思います.
実際の計算結果も興味ある点なので,よろしければぜひ計算過程を示してください.あ,あとUはΔU(内部エネルギーそのものではなくその変化)と書くべきです.
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
重厚にして実務型 さんのレス (2009/08/04(Tue) 10:43)
Yokkunさん,再びご丁寧にありがとうございました.
問題文には「理想気体」としか記述されていなかったので定数扱いするということにします. 変化後の温度は,P[A]*V[A]/T[A]=P[B]*V[B]/T[B]より,T[B]=4T[A]. 気体がその間にした仕事は,それを正として,W=3/2*k*V[A]^2(台形の面積). 内部エネルギーの変化は, ?U=∫[T[A]→T[B]] C[v] dT=C[v](T[B]-T[A])
=3C[v]*T[A].
吸収した熱は,?U-W.
となりました.C[v]がどうしようもないのでこれ以上の変形はどうかと.
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
Yokkun さんのレス (2009/08/04(Tue) 12:11)
>C[v]がどうしようもないのでこれ以上の変形はどうかと.
比熱比 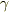 が与えられていますね?これを使ってほしいのだと思います.
が与えられていますね?これを使ってほしいのだと思います.
定圧変化の場合の熱力学第一法則はどうなるか書けますか?
それに状態方程式を適用して 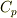 の定義を使うと
の定義を使うと 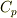 と
と 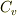 の関係が出てきます.これを
の関係が出てきます.これを 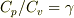 と連立させると
と連立させると 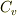 を
を 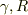 で書き換えることができるのですが,ちょっと考えてみませんか?
で書き換えることができるのですが,ちょっと考えてみませんか?
また, 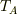 は問題で与えられていませんから状態方程式またはボイル・シャルルの法則を使って
は問題で与えられていませんから状態方程式またはボイル・シャルルの法則を使って 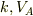 で書き換えましょう.
で書き換えましょう.
Re: 圧力と体積が比例する場合の理想気体の吸収熱と内部エネルギー
重厚にして実務型 さんのレス (2009/08/04(Tue) 13:51)
Yokkunさん,最後まで委曲をつくされた回答をありがとうございました. 最後にご指摘いただいたことも理解でき,改めて書き直して無事解決することができました.なるほどこういうことだったのですね. 感謝いたします.