Euler方程式
Euler方程式
ton さんの書込 (2009/07/28(Tue) 21:16)
大学生です.
L(Lagrangian)が  を含んでいない時(Lは
を含んでいない時(Lは  と
と 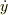 の関数,
の関数,  は
は  の関数とする)
の関数とする)
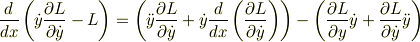
で相殺が起こり,残った項はEulerの方程式により消えるので
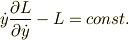
ですが 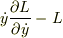 この式はどのように導出するのでしょうか.お願いします.
この式はどのように導出するのでしょうか.お願いします.
Re: Euler方程式
トビラ.. さんのレス (2009/07/28(Tue) 23:34)
これHamiltonianですよね?多分.
僕の知る限りこの式の導出はいくつかあります.例えば,ルジャンドル変換(?,だったかな?)を使う方法で説明すると,まず,ルジャンドル変換とは変数変換のことです.例えば,関数 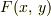 の変数
の変数 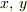 を
を 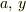 に変えたい場合(ただし,
に変えたい場合(ただし, 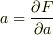 ),の時に行う便利な変換をルジャンドル変換と呼びます.
ルジャンドル変換を具体的に計算すると,
),の時に行う便利な変換をルジャンドル変換と呼びます.
ルジャンドル変換を具体的に計算すると,
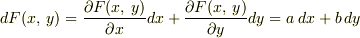 ここで,
ここで, 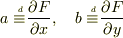 と定義した
と定義した
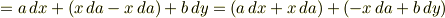
この式の右辺第2括弧の中は 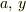 のを変数とする関数の微分と考えることができるから(なぜなら,
のを変数とする関数の微分と考えることができるから(なぜなら, 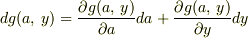 のように微係数
のように微係数 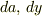 がついているから)
がついているから)

したがって,少し整理して
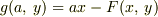 となりますよね?これがルジャンドル変換です.これをルジャンドル変換の公式とここでは呼ぶことにしましょう.
Lagrange関数
となりますよね?これがルジャンドル変換です.これをルジャンドル変換の公式とここでは呼ぶことにしましょう.
Lagrange関数 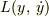 は
は 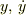 の関数なので,この変数を
の関数なので,この変数を  に変えたい場合.ただしここで,便利のため
に変えたい場合.ただしここで,便利のため 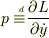 と定義しました.
このように変数を変えたいのであるから先ほどのルジャンドル変換の公式に代入すればよく,代入すると
と定義しました.
このように変数を変えたいのであるから先ほどのルジャンドル変換の公式に代入すればよく,代入すると
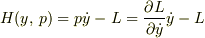 となります.
このようにして,この式がも求まりますが,この関数
となります.
このようにして,この式がも求まりますが,この関数 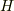 をHamiltonianといい,普通は時間に不変な量.つまり,エネルギーを意味します.
つまり,HamiltonianとはLagrange関数の変数を
をHamiltonianといい,普通は時間に不変な量.つまり,エネルギーを意味します.
つまり,HamiltonianとはLagrange関数の変数を 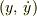 から
から 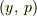 に変えた式ということになります.そうすることにより結構利点などもあります.
に変えた式ということになります.そうすることにより結構利点などもあります.
Re: Euler方程式
ton さんのレス (2009/07/29(Wed) 01:13)
わかりました.ありがとうございました.
Re: Euler方程式
ton さんのレス (2009/07/29(Wed) 20:07)
何度も何度もすみません.最速落下線問題でLagrange 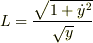 からEulerの方程式
からEulerの方程式
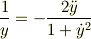
が導かれ両辺に 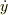 をかけて積分すると
をかけて積分すると
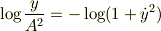
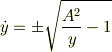
(Aは任意定数)?のように,本来2階の微分方程式であったEulerの方程式が積分されて一階の式に帰着したのはLagrangeが  を含んでいないためであり
を含んでいないためであり 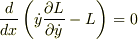 からLagrangeが
からLagrangeが  を含まないときは
を含まないときは 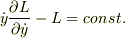 ?となる.
?となる.
で確かに 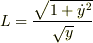 を?式に代入してみると?式と一致するのですが作用積分の第一変分が運動方程式と同値であることはわかるのですがHamiltonianと運動方程式との関係はどのようなものなのでしょうか.お願いします.
を?式に代入してみると?式と一致するのですが作用積分の第一変分が運動方程式と同値であることはわかるのですがHamiltonianと運動方程式との関係はどのようなものなのでしょうか.お願いします.
Re: Euler方程式
トビラ.. さんのレス (2009/07/30(Thu) 02:14)
ごめんなさい,質問がわからなかったです.
>Hamiltonianと運動方程式との関係はどのようなものなのでしょうか.お願いします.
を聞くのに上述の式は必要なのでしょうか?必要だとするとどのような質問なのか僕理解できませんでした.ごめんなさい.
tonさんの質問は好きです.
>この式はどのように導出するのでしょうか.お願いします.
ちょっとしたことでも,どうしてこのようになるのか,を探求する気持ちはとても素晴らしいのでこれからも持ち続けてくれるとうれしいです. こうなるからこうなるんだ深く考えるなっていう人もいますが,僕はそのように考えるのは嫌いです.そうなる意図がしりたいですよね?
で,本題ですけど,以前述べたようにHamiltonianってただLagrange 関数の変数を変えたものでしたよね?ここで,便利のため 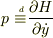 と定義します.
また,したがってHamiltonianは
と定義します.
また,したがってHamiltonianは 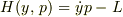 となりますよね
?本当は左辺の変数が
となりますよね
?本当は左辺の変数が 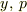 なので,右辺に現れる
なので,右辺に現れる 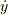 を
を 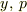 の関数として書き変えなくてはならないんですが,今はこの話は置いときましょう.
僕の知っているHamiltonianを用いた運動方程式は正準運動方程式と呼びます.その式を今から導出しましょう.
の関数として書き変えなくてはならないんですが,今はこの話は置いときましょう.
僕の知っているHamiltonianを用いた運動方程式は正準運動方程式と呼びます.その式を今から導出しましょう.
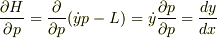
ともうひとつ
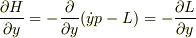 ここで,Lagrenge方程式より
ここで,Lagrenge方程式より 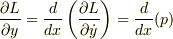 なので,この式を代入すると
なので,この式を代入すると
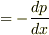 ということになりますよね?この式を並べてみると
ということになりますよね?この式を並べてみると
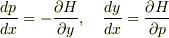 となる.この2つの式がHamiltonianを使った運動方程式だよ.
Lagrange関数を使った運動方程式は
となる.この2つの式がHamiltonianを使った運動方程式だよ.
Lagrange関数を使った運動方程式は 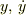 を変数としていたよね?だってLagrange関数の変数が
を変数としていたよね?だってLagrange関数の変数が 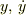 であるから,
でも,今回はHamiltonianを使った運動方程式だから,この運動方程式の変数もHamiltonianの変数にそろえる必要がある.したがって,この運動方程式の変数は
であるから,
でも,今回はHamiltonianを使った運動方程式だから,この運動方程式の変数もHamiltonianの変数にそろえる必要がある.したがって,この運動方程式の変数は 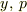 となるんだね.
というか,単純にLagrangeの運動方程式にHamiltonianとLagrange関数との関係式
となるんだね.
というか,単純にLagrangeの運動方程式にHamiltonianとLagrange関数との関係式
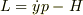 を代入して
を代入して  を消しても上の式の片方は求まりそうだね.
というか,僕の解答が全くの的外れだったらごめんね.
を消しても上の式の片方は求まりそうだね.
というか,僕の解答が全くの的外れだったらごめんね.
Re: Euler方程式
ton さんのレス (2009/07/30(Thu) 03:09)
日本語が下手ですみません.
解析力学はLagrangianの作用積分の第一変分が0というものがNewtonの運動方程式と同値であるということからEulerの方程式を求めて運動の式を導出しているんですよね?
一方,Lagrangianに  が含まれていない時Hamiltonian=const.という条件式にLagrangianを代入するとなぜか作用積分の第一変分が0という条件から導いたEulerの方程式と一致してしまうのです.
HamiltonianはただLagrangianの変数変換させただけなのにHamiltonian=const.という条件式にLagrangianを代入するとEulerの方程式と一致してしまうのはなぜなのでしょうか?
が含まれていない時Hamiltonian=const.という条件式にLagrangianを代入するとなぜか作用積分の第一変分が0という条件から導いたEulerの方程式と一致してしまうのです.
HamiltonianはただLagrangianの変数変換させただけなのにHamiltonian=const.という条件式にLagrangianを代入するとEulerの方程式と一致してしまうのはなぜなのでしょうか?
トビラさん何度も何度も同じ質問をすみません.
Re: Euler方程式
トビラ.. さんのレス (2009/07/30(Thu) 05:22)
ああそういうことですか.つまり,初めに考えた人はどうやってその条件式 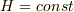 を導出したかってこと?
HamiltonianとLagurange関数との関係式は
を導出したかってこと?
HamiltonianとLagurange関数との関係式は
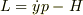 ですよね?これを素直にEulerの方程式(Lgagrange関数の式)に代入すれば,そのEulerの式に対応する
ですよね?これを素直にEulerの方程式(Lgagrange関数の式)に代入すれば,そのEulerの式に対応する 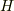 を用いた式つまり,
を用いた式つまり, 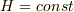 が求まるんじゃないでしょうか?つまり,
が求まるんじゃないでしょうか?つまり, 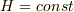 はEulerの式を
はEulerの式を  ではなく
ではなく 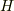 を使って表現した式と解釈すればいいと思いますが.
を使って表現した式と解釈すればいいと思いますが.
それか,次のような証明をtonさんは望んでいるのでしょうか?
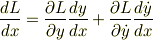
また,Eulerの方程式より 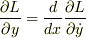 なので
なので
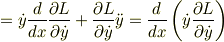
となるので,左辺を右辺に移行して
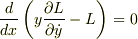 となる.この左辺の括弧の中を
となる.この左辺の括弧の中を 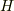 を定義して両辺を
を定義して両辺を  により積分すると
により積分すると 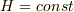 となる.
この
となる.
この 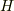 はまた,Lagrage関数の変数を
はまた,Lagrage関数の変数を 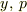 に変えた式と一致するので,Lagrange関数の変数を
に変えた式と一致するので,Lagrange関数の変数を 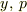 に変えた式だとも解釈できる.ではだめ?
に変えた式だとも解釈できる.ではだめ?
Re: Euler方程式
ton さんのレス (2009/07/30(Thu) 19:12)
を変分原理を使うことでHamiltonianの運動方程式を導くことはわかったのですが
を直接Eulerの方程式に代入して
への式変形がわからないので何かヒントをいただけないでしょうか.
Re: Euler方程式
トビラ.. さんのレス (2009/07/31(Fri) 00:40)
こうゆう時はまず,わかっている方程式を書き出すことがポイントです.ただし単純な式変形で変化させただけの式は書いても意味はありません.独立な式を書き出しましょう.
そうすると今わかっている必要な方程式を書き出すと
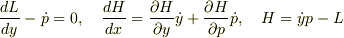 ですよね?
この式の左から順に第1式,第2式,第3式と呼ぶことにすると,おおざっぱに言うと第1式と第3式を用いて
ですよね?
この式の左から順に第1式,第2式,第3式と呼ぶことにすると,おおざっぱに言うと第1式と第3式を用いて  を消して,その式と第2式から
を消して,その式と第2式から 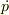 を消せば
を消せば 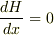 がもとまり,後はこれを積分すればOKです.
がもとまり,後はこれを積分すればOKです.