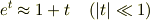無題

home > 掲示板 >

このページのPDF版

サイトマップ

無題

ゆうさんの書込 (2009/07/27(Mon) 19:21)

近似計算の質問になるのですが， eのt乗が，tがものすごい小さい時に，１＋tになる理由を教えてください．計算過程でいいです．お願いします．

Re: 無題

gok さんのレス (2009/07/27(Mon) 20:08)

Taylor展開（Maclaurin展開）は御存知ですか？

近似式

$e^t \approx 1+t \quad \left( \left| t \right| \ll 1 \right)$

は， e^t のMaclaurin展開1次近似を考えれば得られます．

Re: 無題

ゆうさんのレス (2009/07/27(Mon) 20:33)

（1＋ε）のm乗が，εが１よりずっと小さいときに１＋mεになる近似を用いて求めることは可能ですか？

元々無理なら仕方ないのですが・・・・．

Taylor展開は入りだけ少し教えてもらいました．

Re: 無題

toorisugari no Hiro さんのレス (2009/07/27(Mon) 20:55)

横から失礼します．

> eのt乗が，tがものすごい小さい時に，１＋tになる理由を教えてください．

この質問は二つの答え方がありますが，そのうち一つはgokさんが示されたので，もう一つの方．

そうなるように $\mathrm{e}$ の値を決めたからです．

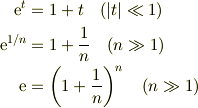
$\mathrm{e}^t &= 1 + t \quad(|t|\ll 1)\\\mathrm{e}^{1/n} &= 1 + \frac{1}{n} \quad(n \gg 1)\\\mathrm{e} &= \left(1 + \frac{1}{n}\right)^n \quad(n \gg 1)$

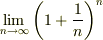$\lim_{n\to \infty}\left(1 + \frac{1}{n}\right)^n$ は計算すると2.71828..となります．これをNepia数と呼びます．

Re: 無題

ゆうさんのレス (2009/07/27(Mon) 22:07)

gokさん，toorisugari no Hiroさん．ご指導ありがとうございます．

お二人の意見を参考いたしまして，やってみたいと思います．急な質問に対応していただき感謝いたします．

Re: 無題

gok さんのレス (2009/07/28(Tue) 00:01)

……よく見直すと，我ながら大変不親切な説明でしたね^^; お節介かも知れませんが補足しておきます．

関数 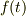f(t) が，ある一定の条件を満たすとき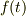， f(t) を次のように無限べき級数で表現することができます．これを 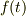f(t) のTaylor展開といいます．

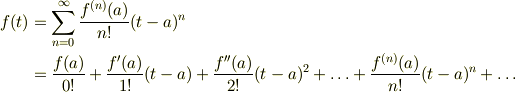
$f(t)&=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(t-a)^{n}\\&=\frac{f(a)}{0!}+\frac{f^{\prime}(a)}{1!}(t-a)+\frac{f^{\prime\prime}(a)}{2!}(t-a)^{2}+\ldots+\frac{f^{(n)}(a)}{n!}(t-a)^{n}+\ldots$

また，特に 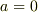a=0 として表現した場合，これをMaclaurin展開といいます．

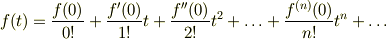
$f(t)=\frac{f(0)}{0!}+\frac{f^{\prime}(0)}{1!}t+\frac{f^{\prime\prime}(0)}{2!}t^{2}+\ldots+\frac{f^{(n)}(0)}{n!}t^{n}+\ldots$

ここで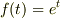， f(t)=e^t については，の値によらず常に

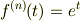
$f^{(n)}(t)=e^t$

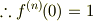
$\therefore f^{(n)}(0)=1$

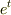が成り立つので， e^t のMaclaurin展開は次のようになります．

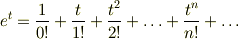
$e^t=\frac{1}{0!}+\frac{t}{1!}+\frac{t^{2}}{2!}+\ldots+\frac{t^{n}}{n!}+\ldots$

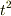よって，が微小であるという仮定を用いて t^2 以上の項を無視すれば（1次近似），

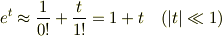
$e^{t}\approx\frac{1}{0!}+\frac{t}{1!}=1+t\quad(\left|t\right|\ll1)$

が得られます．

関数のMaclaurin展開（と，その1次近似）は，他に次のようなものが有名です．高校物理でもお馴染みのものばかりです．

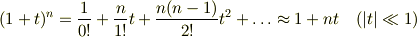
$(1+t)^{n}=\frac{1}{0!}+\frac{n}{1!}t+\frac{n(n-1)}{2!}t^{2}+\ldots\approx1+nt\quad(\left|t\right|\ll1)$

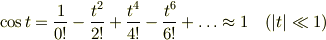
$\cos t=\frac{1}{0!}-\frac{t^{2}}{2!}+\frac{t^{4}}{4!}-\frac{t^{6}}{6!}+\ldots\approx1\quad(\left|t\right|\ll1)$

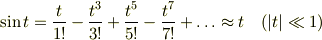
$\sin t=\frac{t}{1!}-\frac{t^{3}}{3!}+\frac{t^{5}}{5!}-\frac{t^{7}}{7!}+\ldots\approx t\quad(\left|t\right|\ll1)$

Re: 無題

toorisugari no Hiro さんのレス (2009/07/28(Tue) 11:33)

gokさんが補足されたので，私もちょっとだけ補足．:-)

> そうなるように |599d333100765b320fed1ae0fe486c0e| の値を決めたからです．

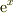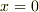高校では $\mathrm{e}^x$ の x=0 における微係数が1になるように $\mathrm{e}$ を定義したと思いますが，おなじ事です．

つまり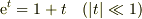， $\mathrm{e}^t &= 1 + t \quad(|t|\ll 1)$ が成り立つなら

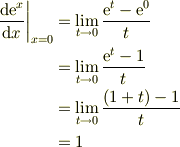
$\left.\frac{\mathrm{d}\mathrm{e}^x}{\mathrm{d}x}\right|_{x=0}&= \lim_{t\to 0}\frac{\mathrm{e}^t-\mathrm{e}^0}{t}\\&= \lim_{t\to 0}\frac{\mathrm{e}^t-1}{t}\\&= \lim_{t\to 0}\frac{(1+t)-1}{t}\\&= 1$

が成り立ちます．逆は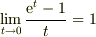， $\lim_{t\to 0}\frac{\mathrm{e}^t-1}{t}=1$ から導けますね．

[home] [掲示板] [ページの先頭]