ダランベールの解 境界条件
ダランベールの解 境界条件
ゆうすけ さんの書込 (2009/07/25(Sat) 00:07)
こんばんわ!妙にはまってしまったので,どなたか回答していただけたら嬉しいです. ダランベールの解に境界条件を当てはめる問題です.(一次元の波について)
両端が開いた開管において,その両端では,ほぼ一定圧力 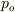 の管外の空気と圧力が等しくなるため,圧力については,境界条件
の管外の空気と圧力が等しくなるため,圧力については,境界条件 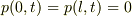 が満たされなければならない.この境界条件を満たすためには,
が満たされなければならない.この境界条件を満たすためには, 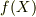 を
を 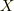 について2階可微分な任意実周期関数
について2階可微分な任意実周期関数 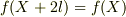 として,
として, 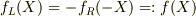 とすれば十分であることを示せ.ただし,
とすれば十分であることを示せ.ただし, 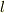 は開管の長さ,ダランベールの解は
は開管の長さ,ダランベールの解は 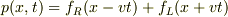 である.
である.
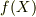 を
を 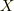 について2階可微分な任意実周期関数
について2階可微分な任意実周期関数 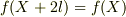 として,
として, 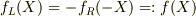 を仮定して,ダランベールの解に代入し,境界条件を満たせばよいと考えたのですが,しっくりとくる答えが出ませんでした.よろしくお願いします.
を仮定して,ダランベールの解に代入し,境界条件を満たせばよいと考えたのですが,しっくりとくる答えが出ませんでした.よろしくお願いします.
Re: ダランベールの解 境界条件
toorisugari no Hiro さんのレス (2009/07/25(Sat) 14:16)
ダランベールの解
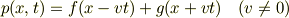
に対して境界条件
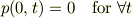
を適用して, 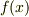 と
と 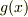 の関係式を導き,
さらに
の関係式を導き,
さらに
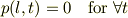
を適用して, 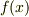 が周期
が周期 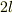 の関数であることが導けますよ.
の関数であることが導けますよ.