全微分について……

全微分について……

チョコレート さんの書込 (2009/07/24(Fri) 16:15)

全微分の言葉の定義や式を見ても全くわかりませんし，イメージがわきません．文系の人でもわかるように説明して頂けたら幸いです．

Re: 全微分について……

DNA さんのレス (2009/07/24(Fri) 17:26)

絵も載ってるのがあると思うが，絵を見てもわからなければ絶対わからんわ． 検索すれば，いくらでも絵がついたやつがあるぞ． それでもわからないならあきらめな．

Re: 全微分について……

toorisugari no Hiro さんのレス (2009/07/24(Fri) 17:58)

\frac{\mathrm{d}f}{\mathrm{d}x} を「微分」と普通いいますね

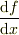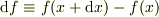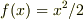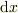でも，正確には， \frac{\mathrm{d}f}{\mathrm{d}x} は微分商あるいは導関数というべきものであり，「微分」とは \mathrm{d}f \equiv f(x+\mathrm{d}x)-f(x) ，つまり微小に離れた場所での関数の「差」を指します． # 例えば f(x)=x^2/2 とすれば， \mathrm{d}x の2乗以上の項は小さいと無視して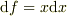， \mathrm{d}f= x\mathrm{d}x ですね．

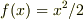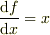ですから導関数は二つの関数/変数の微分(微小な差)の比になります． # 例えば f(x)=x^2/2 とすれば， \frac{\mathrm{d}f}{\mathrm{d}x}= x ですね．

全微分とは以上の考えを2変数以上の関数に拡張したもので，たとえば，2変数関数 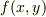f(x,y) の微小に離れた場所での「差」

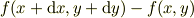
f(x+\mathrm{d}x, y+\mathrm{d}y)-f(x,y)

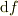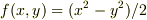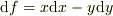などを「全微分」とよび \mathrm{d}f で表します． # 例えば f(x,y)=(x^2-y^2)/2 とすれば， \mathrm{d}f= x\mathrm{d}x-y\mathrm{d}y ですね．

「全微分」とは微小に離れた場所での関数の「差」です．

なぜ，「全微分」を考える必要があるかの説明には，偏微分を導入しなければいけないので，略します．

ただ，覚えておくと良いことは，全微分は微小な量ですが，微小な量が常に全微分(=何かの関数の差)になるわけではない(１変数以外)ということです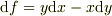． # \mathrm{d}f=y\mathrm{d}x-x\mathrm{d}y となるような f は存在しません．

Re: 全微分について……

チョコレート さんのレス (2009/07/24(Fri) 18:12)

toorisugari no Hiroさんの説明で本が何言いたいのか理解できました．

ありがとうございます．