最小作用の原理
最小作用の原理
pepper さんの書込 (2009/07/23(Thu) 04:43)
大学１年生です． ファインマン物理学３の補章の最小作用の原理についての章を読んだのですが，まず一般的な関数(連続であるとする)を考えた時，極小値で関数をテイラー展開し，XからX+δXに関数を移動させても一回微分が０であるので二回微分から関数がずれていくということを利用していると考えてよいのでしょうか？ そしてδS＝０(ｓは作用)⇔ニュートンの運動方程式とはどういうことなのでしょうか？ わかりやすく書けているのかわりませんがよろしくお願いします．
Re: 最小作用の原理
DNA さんのレス (2009/07/23(Thu) 07:23)
タイトルを自分で的確に書けるぐらいだから，ここで聞くまでもないと思うけど，そのように思いません？ 自分で調べることをしないの？本もいっぱいあるのに不思議だね．
Re: 最小作用の原理
toorisugari no Hiro さんのレス (2009/07/23(Thu) 11:08)
> 二回微分から関数がずれていくということを利用していると考えてよいのでしょうか？
そうです．局所的な「放物線」の底にあるという考えです．
ほかにも似たような考え方があります．
例えば，ポテンシャル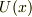 
による保存力と空気抵抗による運動を考えた場合，十分時間が経ったときどこに物体があるかも同じように考えられます．
物体の力学的エネルギーは(そして結果的に位置エネルギーは)熱に奪われ，速度は0に，位置は 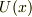が極小となる 
(のどれか)にあります．
つまり，「安定に静止する物体の位置エネルギーは極小である．(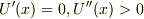 
)」といえます．
> そしてδS＝０(ｓは作用)⇔ニュートンの運動方程式とはどういうことなのでしょうか？
これは難しい．うまく答えられません．
ただ，光の経路などの観測から得られる光路長の原理，上に述べた位置エネルギー最小原理から，運動も「何かを最小にしているのではないか」と考え，
位置エネルギーがあり，位置エネルギー最小原理から位置の方程式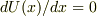 
が得られるように，「作用」というものがあり，「作用最小原理」から運動方程式 ![\delta S[q]/\delta q=0](http://hooktail.maxwell.jp/bbslog/9c18a6839c78eb1b8e8e84fe63691215.png)
が得られると考えるのは自然だと思います．
# は位置を表す「実数」， 
は軌道を表す「実数値関数」
そしてラグランジアン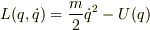 
を積分した「作用」 ![\left(S[q]=\int L(q,\dot q)\mathrm{d}t\right)](http://hooktail.maxwell.jp/bbslog/8257419d6b8d7bcbffa71865270bb837.png)
が上の要求を満たすという「発見」があって，解析力学が生まれたと私は思います．
なぜ，作用が運動を記述できるのか?なぜラグランジアンがこのような関数形なのか?世の中がそうなっているからとしか私にはいえません．
