jedi さんの書込 (2009/07/21(Tue) 17:50)

高3です． コイルを交流電源につないで電圧をかけたとき， コイルの自己誘導で逆起電力が生じますが，それと電源電圧が釣り合い， 回路全体の起電力の和が0なのに，電流が流れることにどうしても違和感を感じてしまいます． 数式がそう言ってるのだから，疑問を抱く必要はない， ということにはどうしてもできません． 微視的に見てみると何が起こっているのでしょう？ うまく説明していただけないでしょうか？

mNeji さんのレス (2009/07/21(Tue) 20:10)

jediさん，面白い論点だとおもいます．

＞回路全体の起電力の和が0なのに，電流が流れることにどうしても違和感を感じてしまいます．

起電力は，交流電源一つと考えて良いとおもいます．

確かに，コイルでは逆起電力といい，コンデンサではそう言いませんが，コンデンサだって電荷が作る逆起電力が交流電源と釣り合うように逆起電力がでると考えることもできますね．

抵抗だって，ポテンシャル差に匹敵する電位差ができるとも考えられそうです．

一寸，説明を考えさせてください．

jedi さんのレス (2009/07/22(Wed) 16:06)

回答ありがとうございます．

＞コンデンサだって電荷が作る逆起電力が交流電源と釣り合うように逆起電力がでると考えることもできますね． 確かに，直流だとその逆起電力で電流が流れなくなりますね．

電流が流れようとしなければコイルの逆起電力は生じませんから， やはり，電流は流れなければいけないんですけどね…．

mNeji さんのレス (2009/07/22(Wed) 16:33)

＞確かに，直流だとその逆起電力で電流が流れなくなりますね．

これはコンデンサの場合の説明ならば，私もそういうイメージです．

＞電流が流れようとしなければコイルの逆起電力は生じませんから， ＞やはり，電流は流れなければいけないんですけどね…．

まだ，さぼっていて考えが纏まっていないのですが...．これから外出するので，明日まで待って下さい．若い頃には十分に理解していた積もりなのに，忘れている(汗)．

mNeji さんのレス (2009/07/22(Wed) 19:03)

少し論議を進めます．

＞回路全体の起電力の和が0なのに，電流が流れることにどうしても違和感を感じてしまいます．

仰る通りなら，電流はゼロになります．交流電源で考えると，数学的準備(複素数の計算に過ぎませんが...)があれば簡単な話です．他方，直流電源で考えると，1次の微分方程式なので，高校の数学の範囲(以前，高校生さんが変数分離法をご存知だったと記憶しているので)でも説明が可能だとおもいーます．

せめて，雰囲気だけでも判れば良いのですが...．

<pre>図１回路の全体

コイル: L ← ┌ーーーーーー┐電流：I(t) ｜｜↑┌−−−┐ ｜｜ａ' ←ａ｜｜↑ ↓｜磁束Φ└ーーーーー┘ｔ｜＋ ｜画面から手前┌ーーーーー┐┌ー┷ーー┐ ｜｜ｂ' →ｂ｜｜電池E(t)｜ ｜｜Ｒ└ー┬ーー┘ └ーーーーーー┘ｃ｜ｇ｜ー →└−−−┘ →

ｇから見たｔの電位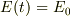＝ ｂから見たａの電位＝コイルの逆起電力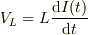＝ ｃから見たｂの電位＝抵抗の電圧降下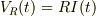＝ </pre>

時刻,t=0まで，理想的な電池は外されていて，その後，t=0以後，回路に接続されたとします．

従って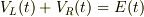， だから

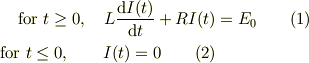
となります．式(1)は一見簡単そうですが，意外と難しい(E0は強制項)ので，左辺に移項して，

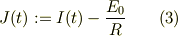
を導入すると式(1)は，

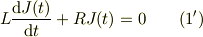
となります．この微分方程式は直接に積分出来て；

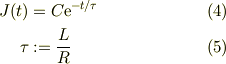
＃ は時間の次元をもつ定数で，「LRの時定数」とも呼ばれます．

式(3)で元に戻して，初期条件(2)を適用して，

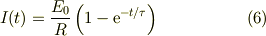
となります．時間t=0で電流はゼロですが，指数関数的に増加し，最後には，コイルが無い場合の電流に収束します．

＃式(6)が微分方程式(1)や初期条件(2)を満足する事だけは，ご自分で手計算して確かめておいて下さい．

そこで，式(6)をコイルの逆起電力に代入すると；

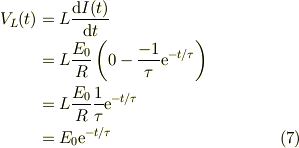
となります．

確かに，t=0で電流がゼロの場合には，逆起電力が電源電圧に等しくなっていて，正に仰る通りですね．しかし，電流が指数関数的増加するにつれて，コイル逆起電力は指数関数的に減少し，その分，抵抗で発生する電圧降下分が指数関数的に増加しています．ちなみに，電圧降下分は；

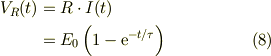
ですね．

コイルの大雑把な挙動はこんな所でしょう．

そもそも『「L」の起源は？』がお知りになりたいとは思いますが，電磁誘導の式を利用しないといけないので，大学生になってから勉強されるといいと思いますが...．

ミュフ猫 さんのレス (2009/07/22(Wed) 21:32)

jediさん，こんばんは．

コイルという回路素子は，キャリアである荷電粒子に対し，強制的に螺旋軌道を 描かせる必要があるため，構造上，内部抵抗が存在する素材を使用せざるを得な いのではないかと思います． ですから，理論上は近似的に内部抵抗を排除していても，実際はコイルの両端に 内部抵抗分の電位差が存在し，それに相当する電場がコイル内に生じているのでは ないでしょうか？ ちなみに，もし，螺旋軌道を描かせることができて，かつ抵抗がない素材が見つ かっても，理論値道理には動作しないと思います． なぜならば，その場合，伝導電流の性質（オームの法則）が前面に現れていたお かげで失われていた，本来，荷電粒子が持つ質量慣性が新たな運動の法則として 入れ替わってしまうので，単に，抵抗値０を近似しただけの理論値とは，かなり 食い違って来ると思うからです．

間違ってたらすいません・・・．ｗ

jedi さんのレス (2009/07/23(Thu) 00:58)

回答ありがとうございます． キルヒホッフの第2法則を用いて，微分方程式を解けば(変数分離というのは知っています) 数式的には導けるのですが，どうも定性的なイメージがわかないのです…． コイルを直流電源に繋いだときの定性的なイメージはできます． しかし，交流電源に繋いだときが，定量的には導けても，定性的なイメージができないのです…．

Lの起源というのは一応教科書で導きましたが， つまりLI=φということですよね？

mNeji さんのレス (2009/07/23(Thu) 02:16)

＞数式的には導けるのですが，どうも定性的なイメージがわかないのです…． ＞コイルを直流電源に繋いだときの定性的なイメージはできます．

これは参りました．恐らく，高校生さんのレベルを越えているようですね．直流電源に対する応答をイメージ出来ているということは，過渡(かと)応答を理解されているという事で素晴らしいですよ．

そういう事なら，十分に電源につなげて放置した後に，電源電圧を 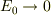とした時の電流応答を考えて見てください．

○ヒント

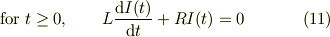
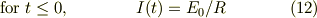
もし，上が出来ると， ＞しかし，交流電源に繋いだときが，定量的には導けても，定性的なイメージができないのです…．

ということですが；

・もしも細かく電源を少しずつあげたり，下げたり出来れば ・直流電源で，交流電源をシミュレートできる？

と考えられませんか？

もう少し，違った言い方をすれば，交流の電源電圧変化に対して， ・コンデンサは電流の積分の為に，応答が遅れる． ・コイルでは電流の微分の為に，応答が進む． といった見方ができるでしょう．

でも，あまり定性的な理解を押し進めるのは，どうなんでしょうか．

複素数の指数関数表現を使って考えた方が，良いと思います．

＞Lの起源というのは一応教科書で導きましたが， ＞つまりLI=φということですよね？

あ，そうです．なんという出版社の，何年版の教科書でしょうか？

＃いずれにしろ，微分積分には余裕を感じられていると思われます．それなら， ＃物理の細かな理解を整備するよりも，数学・語学・運動・常識など，若い頃にしか出来ない領域にも， ＃積極的にトライされる事を強くお勧めします． ＃ ＃(そう出来なかった経験者の自己反省)

ASA さんのレス (2009/07/23(Thu) 07:36)

別の場所でも書きましたが，力学系との対応で理解するのがベストと考えます． E=L(dI/dt); 電界は，単位電荷を基準にすると力の次元を持ちます． そうすると，力学の法則 F=m(dv/dt);E→F,L→m,v→I と対応がつきます(力学を基本的な枠組みとして電磁気学が整備された)．

交流電源は，力学で考えると，強制振動現象です． これは，折り返し点で最も力が強く，速度が最高のときは，力が働きません． 振り子を手で強制振動させれば，実感できます． (高校向けの参考書には，力学との対応は載っているはずですが)

>定性的な理解を押し進めるのは，どうなんでしょうか． 物理は，自然と対応した定性的な理解がベースである考えています．

jedi さんのレス (2009/07/23(Thu) 22:20)

回答ありがとうございます． 少しじっくり考えてみることにします． 教科書は数研出版の「改訂版 高等学校 物理?」平成20年1月10日発行版です． 先生が言うにはこの教科書は高校の教科書の中ではマニアックらしいです． コイル内の"磁場に"蓄えられるエネルギーという記載があったり， 交流回路にスピーカーの話が載っていたり，という点がそのようです． ただ，私は他の教科書を見たことがないので何とも言えません．

mNeji さんのレス (2009/07/23(Thu) 23:24)

＞少しじっくり考えてみることにします．

考えが纏まったら，論議を続けましょう．恐らく，似た様な論議をコンデンサーに付いてもして，コイルとコンデンサーの振る舞いを比較するとイメージが明確に出来ると思います．楽しんで下さい．

＞教科書は数研出版の「改訂版 高等学校 物理?」平成20年1月10日発行版です．

ご教示感謝します．この少し前の版は購入してあるので，探してみます．

＞先生が言うにはこの教科書は高校の教科書の中ではマニアックらしいです． ＞コイル内の"磁場に"蓄えられるエネルギーという記載があったり，

なるほど，この関連の論議は，今回の様な回路で十分時間が経ってからヒントとして出した様に とした時に流れる電流の根拠(電源電圧がゼロVなのに電流が流れるのですから！)と考えることが出来ると思います．

＞交流回路にスピーカーの話が載っていたり，という点がそのようです．

ヴォイス・コイルの話でしょうかね．

jedi さんのレス (2009/07/26(Sun) 23:51)

こんばんわ． 私の疑問にお付き合いいただきありがとうございます．

微妙に掴めてきました． ただ，本当に微妙なんで油断するとパッと消えてしまいそうです．

電源電圧と逆起電力が釣り合うことによって電流の大きさが決まるわけですね． 逆起電力がないとなると，思考上電流は正の無限大から瞬間的に負の無限大になったり，その逆のことが起こったりしますから．

ただ，釣り合うことによって電流の大きさが決まるとなると， 位相のずれがイメージできません． もう少し思案してみます．

mNeji さんのレス (2009/07/27(Mon) 00:03)

＞微妙に掴めてきました． ＞ただ，本当に微妙なんで油断するとパッと消えてしまいそうです．

きっと，こういった「ふらふら感覚」に耐える事が大切なのだと思います．なんども行ったり，来たり，グルグルと廻っている内に，段々と霧が晴れて来る様な...．

＞電源電圧と逆起電力が釣り合うことによって電流の大きさが決まるわけですね．

例えば，重力下で落下する雨粒も，重力で下がる為に速度がでて，その速度の為に摩擦機構により減速して加速度が変わって，段々と速度が収束していって...．これも微分方程式で記述できるから」当たり前のようですが，式を使えないと結構イメージが難しいですよね．

＃ただし，動き出す切っ掛けはあくまで「重力」ですね．回路でいえば電池の「起電力」に対応するのでしょうね．

＃「コイルが動いても，電流が動いても電位を生じるメカニズム」としての「電磁誘導」が雨粒での「摩擦機構」に対応する感じでしょうかね．

＃で，結局，電位と電流の関係の微分方程式を解いてから，其れを解釈するというステップを踏まないと，正しい理解を得られないという結論になってしまうような...．

＞ただ，釣り合うことによって電流の大きさが決まるとなると， ＞位相のずれがイメージできません．

これは，別の問題として，現段階では棚上げして置きませんか．でも某国の首相と違って，この問題から逃げませんので，安心して下さい(笑)．

ミュフ猫 さんのレス (2009/07/27(Mon) 00:41)

>電源電圧と逆起電力が釣り合うことによって電流の大きさが決まるわけですね．

あのー．その「逆起電力」がコイルの誘導起電力のみを意味しておられるのなら， 違うの思うのですが・・・．

mNeji さんのレス (2009/07/27(Mon) 00:52)

ミュフ猫さん，

＞あのー．その「逆起電力」がコイルの誘導起電力のみを意味しておられるのなら， ＞違うの思うのですが・・・．

私には良く理解出来ないのですが，お説を式にして表してくださると有難いのですが，如何でしょうか？少し位の長さなら大丈夫だと思います．かなり長くなりそうでしたら，別にスレッドを立ち上げる方がいいかも知れませんが．

ミュフ猫 さんのレス (2009/07/27(Mon) 01:47)

mNejiさん，こんばんは．

まず，誘導起電力を生じさせるためには，コイル内で電流が時間変動する 必要があります． コイルには内部抵抗が存在しますから，当然，コイルの両端に生じる電荷 の偏りのうち，内部抵抗分に相当するものがもたらす電位差もまた，その 電流と同位相で時間変動します．（オームの法則ですね．）

一方，コイル内の合成電場の成分の一つである誘導電場は，合成電場と位相が ズレます．（コイル内の合成電場の位相が，電流のそれに一致するからですね．） 電源電圧が直にコイルの両端に接続されている回路をモデルとして考えると， 電源電圧と実際のコイルの両端の電位差（内部抵抗分の電位差＋誘導起電力） が同じ（つまり，同位相，同振幅）で，釣り合うわけですから，電源電圧と 誘導起電力（つまり，誘導電場×コイル長）とは，位相が異なると思う のですが・・・．

おそらく，「内部抵抗は無視する」と突っ込まれるかもしれませんが， そもそも，誘導電場を生じさせるためには，内部抵抗が必要なわけで， コイルという回路素子は，自己誘導係数 Lと内部抵抗値 Rを併せ持つ， 二つで一つの合成回路素子と考えた方が，理屈に合う気がするのです．

mNeji さんのレス (2009/07/27(Mon) 02:53)

ミュフ猫さん，

回路での素子の動作を考えるのは，難しい問題だと思います．私自身，中学から高校にかけてアマチュア無線に凝っていた時期があり，悩みました．それなりに理解した積もりだったのですが，今回の jediさんのご質問で問題の再考をせまられていて，どぎまぎしています．

さて，実際の回路での動作では，コイルの場合でも，浮遊静電容量(コンデンサ)や抵抗成分を考える事があります．特に高周波数での挙動では，コイルとコンデンサが変わったりします．抵抗成分は，共振点の近くや，今回の様に過渡応答で重要になります．

また，抵抗成分は電源自体がもつ抵抗もあり，私は，回路の場合は，純粋なコイルやコンデンサに直列に明示的な抵抗をいれて実験したり，解析するようにしています．

ですから，事前に「無限大の電流」は回避するようにしています．恐らく，超伝導コイルを励磁する場合などを調べれば，「内部抵抗がゼロ」のコイルをどうやって運転するか判ると思います．

他方，逆起電力のメカニズムについては，「ファラデイさんの電磁誘導」以外については存じ上げませんので，悪しからず．

ミュフ猫 さんのレス (2009/07/27(Mon) 07:53)

mNejiさん，おはようございます．

どうも，誤解があったようなので説明します． 私の発言，

「その「逆起電力」がコイルの誘導起電力のみを意味しておられるのなら， 違うの思うのですが・・・． 」

の真意は，

「電源電圧と誘導起電力は厳密に釣り合わないと思います．」

ということで，

「逆起電力は誘導起電力を意味する用語ではないと思うのです．」

ではありません．当然，「逆起電力」は「誘導起電力」と同義だと思います．

>恐らく，超伝導コイルを励磁する場合などを調べれば，「内部抵抗がゼロ」 >のコイルをどうやって運転するか判ると思います．

これは，

「誘導電場を生じさせるには，必ずしも，内部抵抗が必要とは限らない．」

と仰りたいのですね？なるほど，勉強不足ですみません． しかし，コイルが発明された当初，いきなり，超伝導コイルが誕生した わけではなく，まず，内部抵抗をもつ，単純な螺旋構造の導線コイル のようなものではなかったでしょうか？ 当時の物理学者も，内部抵抗は百も承知で，電気回路理論を展開したと 思います． 私は質問者のjediさんの最初の書き込みの疑問に対し，

「任意の時刻で，電源電圧と誘導起電力が釣り合うなら，誘導電場 どころかコイル内に合成電場は生じず，電流は流れないはず． 百歩譲って，内部抵抗値０を仮定しても，電流は定常的になり， やはり誘導電場は生じない．これは，どういうことだろう？」

という意味に受け取りました． この解釈は間違いでしょうか？なら，私の書き込みは無意味です．

ASA さんのレス (2009/07/27(Mon) 08:01)

mNejiさんの説明では，初学者を余計混乱させている気がします．

なんども書きますが，力学系との対応で理解するのがベストです． F:外部電源電圧,コイル,抵抗,コンデンサでの回路は，I→vの対応で F=L(dI/dt)+RI+C1(∫Idt)と記述できます(C1；比例定数)． ちなみに，∫Idt=Q→x;位置に対応ですから コンデンサーによる力は，力学系対応ではg(x)と位置の関数であるからポテンシャル(位置エネルギー)による力，電気的にはいわゆる電位です． そこで，比例定数C１→1/C;(C;キャパシタンス）と置いて(逆数なことに注意)． F=L(dI/dt)+RI+(∫Idt)/C と線形微分方程式の問題に還元できます．

超伝導コイルでは，抵抗Rが0でも F=L(dI/dt) なので 無限の起電力F(有限の場合は∞時間をかけてエネルギーを蓄積していく)を与えない限り，電流Iは無限になりません． 抵抗は，静的釣り合いで理解できますが，コイルは誘導法則により時間変化が鍵となので，動的釣り合いで理解しなければいけません．

mNeji さんのレス (2009/07/27(Mon) 08:58)

ASAさん，

＞なんども書きますが，力学系との対応で理解するのがベストです．

実は，私も勉強したての頃(大昔)，この考え方に従ったのですが，逆の結論になりました．

その要点は，コイルの動作，明示的にいえば，電磁誘導の動作には，力学的な対応が無いことだと思います．最終的な微分方程式の形式が同じだからという事と，現象を理解出来るという事は違う様に思います．

恐らく，昔の勉強の進度では，力学系が先に教えられたので，良く知っている力学系の微分方程式に対比させて，電磁気学の現象を理解させようとしたのではないでしょうか？

少なくとも，１次線形微分方程式を変数分離で処理する能力があれば，力学的類推を用いなくても，電磁誘導の一例として，起電力と電流との関係を微分方程式にして表現し，それを解き，解釈出来ると思うのですが...．

なお，超伝導コイルの問題は，私も良く知りません．できれば，別のスレッドでご教示くだされば幸いです．

mNeji さんのレス (2009/07/27(Mon) 12:02)

ミュフ猫さん，

コメントを見過ごしていました，ご免なさい．

＞「任意の時刻で，電源電圧と誘導起電力が釣り合うなら，誘導電場 どころかコイル内に合成電場は生じず，電流は流れないはず． 百歩譲って，内部抵抗値０を仮定しても，電流は定常的になり， やはり誘導電場は生じない．これは，どういうことだろう？」

＞という意味に受け取りました． ＞この解釈は間違いでしょうか？なら，私の書き込みは無意味です．

ああ，この問いかけこそが，多くの人々を悩ませて来た切り口だと思います．

一寸話が飛びますが，自分自身は，今回の論議で出て来たような電源電圧のステップ応答から，コンデンサやコイルの特徴を理解出来るという経験的な感触を持っていたのですが，微分方程式の理解が深くないので，説明を躊躇していました．ただ，最近になって，線形定数係数微分方程式が因数分解出来るという事に目覚めてから，常微分方程式を再勉強中であります．その目でいえば，1次定数係数微分方程式が解ければ，一般的なn次定数係数微分方程式も解ける．また，高校の数学の段階で，変数分離を解ける事を知り，其れならば，「コイル＋抵抗」という系のステップ応答で，お書きになった設問を説明出来るのではないかという立場におります．

ASA さんのレス (2009/07/27(Mon) 19:10)

コイルに交流電圧をかけるのは，力学系だと単純な強制振動の問題です． F=m(dv/dt)；F=fsinωtなら，v=Acosωtです． 慣性力:m(dv/dt)と強制力:Fは，常に等しい(作用反作用の法則から，足せば0）ですが，そのため運動しない(v=0)ということではありません． 慣性の法則から，運動状態を変化させるときにこそ力が必要なので，速度と力とでは位相がずれているわけです．

なお，インダクタンスLは電磁気的慣性の大きさを表わしている理解できます．

このような理解の元では，電気回路でのみ疑問に思い，なぜ，力学系で疑問に思わないのかが不思議です．

jedi さんのレス (2009/07/27(Mon) 19:30)

こんばんわ．大分進んでいますね． 興味を持っていただきありがとうございます．

もう1ヶ月程考えているのですが， なかなか晴れない疑問をもう1度整理して書かせていただきます．

"交流電源にコイルを繋ぐと， 電源電圧とコイルの誘導起電力が釣り合って電流が流れないのではないか？" (電源の内部抵抗，コイルの内部抵抗，導線の抵抗は考えない)

例えばコンデンサーを直流電源に繋ぐ場合， コンデンサーの逆起電力が電源電圧と釣り合えば電流は流れなくなります．

では，コイルを交流電源に繋ぐ場合は，

Vsinωt-L(dI/dt)=0

で，やはり釣り合って流れない…ということはなく 実際には流れるんですねぇ，これが．

ちょっと疲れてきました． ここに書き込みをさせていただく以前にもかなり調べて考え込んでいましたので…． しかし，放棄するわけにはいきません． 高校の電磁気に関してはこの一点だけが晴れず， 何とか夏休みが終わるまでには解決したいのです． それでは，また考え込んできます...

mNeji さんのレス (2009/07/27(Mon) 20:36)

う〜む，私の想像していた問題意識と違う様ですね．色々な切り口があるということでしょうね．

＞"交流電源にコイルを繋ぐと， ＞電源電圧とコイルの誘導起電力が釣り合って電流が流れないのではないか？" ＞(電源の内部抵抗，コイルの内部抵抗，導線の抵抗は考えない)

No.24813で書いた絵で，「電池E(t)」と書いた様に，この図や微分方程式は直流であろうが，交流であろうが成立します．これは納得できますか？

私が高校生の時にも，直流と交流で振る舞いが違う様に考えた記憶があります．今回の提案では，直流のステップ応答を組み合わせて， <pre> ↑E(t)

E0┌ーーーーー┐┌ーー以右略 ｜｜｜ ｜｜｜ ｜｜｜ ｜｜｜ ーーーーーーー・ーーーーー＋ーーーーー＋ーーーーー→t t=0 ｜ t=T｜t=2T ｜｜ ｜｜ ｜｜

-E0└ーーーーー┘

</pre>

と考えると，交流応答をステップ応答の組み合わせでイメージできると思った訳です．

＞例えばコンデンサーを直流電源に繋ぐ場合， ＞コンデンサーの逆起電力が電源電圧と釣り合えば電流は流れなくなります．

コイルの場合は，直流電源に繋いだ瞬間(電位をステップした時)に「逆起電力が電源電圧と釣り合い，電流はゼロですが，電流の変化率は最大」です．時間の経過にともなって，電流は最大になりますが，逆起電力はゼロになるだけです．

＞では，コイルを交流電源に繋ぐ場合は， ＞Vsinωt-L(dI/dt)=0 ＞で，やはり釣り合って流れない…ということはなく ＞実際には流れるんですねぇ，これが．

そうです，ASAさんが， No.24882で述べられている通りだとおもいます．

細かい事をいえば，初期条件できまる状態(E(t)=0の解，同次解)は指数関数的に減少する為に，長い時間に渡り，交流を加え続けると定常状態になることを利用しています．

〜〜〜〜 やはり，大学の電磁気学で電磁誘導の式を理解してから，再度この問題を考察することをお勧めします．

HNを拝見したとき，自然と「ジェダイさん」と読んでいて，ふと気が付いて検索したら，格調のあるお名前でしたね．

Yokkun さんのレス (2009/07/27(Mon) 23:01)

jediさん，疑問に対する私の解釈が間違っていなければASAさんのおっしゃった「動的平衡」にカギがあるのではないでしょうか？

抵抗を流れる電流の場合も同じことですが，直流電圧に対し微視的には電子は様々な速さで応答しています．しかし，平均として電流が一定に保たれるのは遅すぎる電子に対しては外部電場が抵抗に勝って加速し，速すぎる電子に対しては抵抗が外部電場に勝って減速をするという動的な平衡が成り立っているからだと思います． ASAさんがこれを「静的な平衡（つりあい）」といったのは，時間的空間的に巨視的なスケールにおいて平均をとった上での解釈ですね?

今回の問題についても同様で，微視的な解釈は難しそうですが，要は逆起電力が小さければそれを大きくする作用が働き，外部電圧に対して大きすぎれば小さくする作用が働くことはすぐにわかると思います．

動的な平衡の概念は自然現象の理解にとってとても大切なもので，見かけ上「つりあっている」といえるような現象の多くにおいて当てはまるものです．化学平衡や状態変化の平衡，捕食者と被食者のつりあい…等々．いずれの場合も静的なつりあいと見ると「運動」が継続していることが不思議に思えてしまったりするものです．

的外れでしたら読み捨ててください．

mNeji さんのレス (2009/07/28(Tue) 08:05)

jediさん，

もう一度，初めの問を読んでみました．途中から位相差の話がメインの疑問かと思って歌のですが，やはり「逆起電力」の考え方を知りたいのだ思いましたが，如何ですか．

この問題の本質は，電源電圧に駆動される電流が，それに伴ってコイルを貫通する磁束密度を生じ，その面内に電流に比例した磁束を生じていることです．その磁束の時間変化が逆起電力を生んでいるというのが電磁誘導です．

もう一度詳しく現象を考えます；

始め，完全に電流の無い状態から，電源電位をステップ上昇させる(0→E0)と，電流はゼロから段々と上昇し，同時に大きな逆起電力を生じています．時間が進行すると，電流の上昇率は減少して，逆起電力も減少します．十分時間が経てば，電流は最大値となり，逆起電力はゼロとなっています．この電流に伴って保持される磁束によって磁場にエネルギが蓄えられていると考えられます．以下これを磁場のエネルギと呼びます．

そこで，電源電位をステップ下降させる(E0→0)とします．もはや電源がないにも関わらず電流は，方向はそのままで徐々に減少します．抵抗負荷ではこんな事は出来ませんね．この現象は，磁場のエネルギが解放されて電流を発生するものです．その電流を駆動するのが「コイルの逆起電力」です．

ここで注意するべきは，このステップ下降時には「磁束は時間に伴って減少する」のですから「ステップ下降での逆起電力」は「ステップ上昇での逆起電力(電源電圧に対抗する方向)」の逆，従って，「ステップ下降での逆起電力」は電源電圧と同方向に作用するという結果になります．

丁寧に考えると，このような複雑な話になります．だから初等電磁気の範囲では，コイルの動作を話題にしないのだろうと思います．でも，骨子は「電磁誘導の法則」，

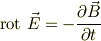
をコイルに適用する事で出て来ます．

同じように，コンデンサの場合も考える事が出来ます．コンデンサに電源電位をステップ上昇させ(0→E0)ると初めは充電電流がながれるものの，十分に時間が経てば電流は流れなくなります．電極間に電束が形成されます．従って電場エネルギーが保持されます．電場は，磁場のように電流を必要としないので電源なしで電場エネルギを保持出来ます．

電源電位をステップ下降させる(E0→0)と，電場エネルギを解放させながら，逆方向の電流を放出します．

他方，抵抗は，電流が流れている間は，電圧降下を起こし，ジュール発熱の形で電源からエネルギを受け取ります．電源が切られると，コイルやコンデンサに蓄えられた電場や磁場のエネルギをジュール発熱で消費します．其のおかげて，初期条件で付与された状態は，ある時定数をもって減少するとも考えられます．

従って，交流回路も安心して，定常的な応答を考えられます．なお，交流回路を考える時には，複素インピーダンスという考え方で，直流の抵抗と似た様な形式で操作しますので，高校の段階で，あまり心配する必要はないように思います．

〜〜〜〜 このような説明は初めて書いたので，変な所や間違いもあると思います．判らない点も含めて論議下されば，幸いです．

ミュフ猫 さんのレス (2009/07/28(Tue) 11:04)

皆さん，こんにちは．

昔，私もLC回路の電気振動現象を不思議に感じ悩みました． そして，RLC直列回路の物理現象を解析し，概ね理解できたつもりです． つまり，LC回路は，現実に起こりうるRLC直列回路の物理現象に対し， R→０という近似を施した仮想的な物理現象だと気づきました． 以前にも書きましたが，コイルは自己誘導係数Lと内部抵抗値Rを 併せ持つ，二つで一つの合成回路素子で，内部抵抗の存在が， コイル内の電磁誘導現象を引き起こす上で必要不可欠な要素と なっており，これを無視して，そのメカニズムを理解するのは， 極めて困難なことかと存じますが・・・．

しつこく同じことを何度も書き込んですみません・・・．

mNeji さんのレス (2009/07/28(Tue) 11:19)

＞以前にも書きましたが，コイルは自己誘導係数Lと内部抵抗値Rを ＞併せ持つ，二つで一つの合成回路素子で，内部抵抗の存在が， ＞コイル内の電磁誘導現象を引き起こす上で必要不可欠な要素と ＞なっており，これを無視して，そのメカニズムを理解するのは， ＞極めて困難なことかと存じますが・・・．

これは興味深いお話ですので，別スレッドにして，詳しく具体的にご説明願えませんか．

ASA さんのレス (2009/07/28(Tue) 11:59)

mNejiさん No.24894

全体的に説明がおかしいですが，目立った間違いを指摘します． >始め，完全に電流の無い状態から，電源電位をステップ上昇させる(0→E0)と，電流はゼロから段々と上昇し，同時に大きな逆起電力を生じています．時間が進行すると，電流の上昇率は減少して，逆起電力も減少します．十分時間が経てば，電流は最大値となり，逆起電力はゼロとなっています．

E0=L(dI/dt) ですから，I=(E0/L)t;t>0(t=0,I=0) 電流の上昇率は (E0/L)で一定です． 何を指して逆起電力といってるのか不明です．

同様にE0→0での説明もおかしいです．

同様にコンデンサの説明も変です．

また，電源と電流の関係も疑問に思えるので，整理して下さい．

mNeji さんのレス (2009/07/28(Tue) 12:40)

ASAさん，

私は，以前の自分の説明，No.24813の，図1と式(1),(2)を前提にして話をしています．そして解については式(6),(7),(8)に示しており，その意味を説明しようとしています．

これは，私の経験では，交流の定常応答を理解する為にも，ステップ応答の仕組みを理解した方が，明快なイメージを組上げられると思うからです．

もちろん，ASAさんのやり方が交流の解析に正統的だろうとは思っていますので，並行的に論議ができればいいのではないでしょうか？

【追伸】

やや誤解をされている様なので...

＞E0=L(dI/dt) ですから，I=(E0/L)t;t>0(t=0,I=0) 電流の上昇率は (E0/L)で一定です． 何を指して逆起電力といってるのか不明です．

仮にそのように考えたとしても，では電流はどこまで上昇するのでしょうか？

そのような状況を避ける為に，コイルとかコンデンサのような素子には通常抵抗をいれて論議するのだと思います．

確かに交流成分だけで考えていれば善いかも知れませんが，そのような教育をしておくと，実際の実験で電源を壊したり，コイルを切ったりするように思います．

「何を指して逆起電力」とは正に，コイルの発生する起電力の事です．

ASA さんのレス (2009/07/28(Tue) 16:15)

mNejiさん

>ステップ応答の仕組みを理解した方が，明快なイメージを組上げられると思うからです． これはさほど問題視してません．

ミュフ猫 さんは，内部抵抗の存在が電磁誘導現象で必要不可欠と考えているようですが，mNejiさんも同様に必要不可欠と考えておられるのでしょうか？ もし，不必要と考えているなら，省いて説明した方が初学者に本質が判りやすい説明になると考えます．

例えば，誤解を受けやすい表現として >電流は最大値となり，逆起電力はゼロとなっています．この電流に伴って保持される磁束によって磁場にエネルギが蓄えられていると考えられます 「この電流」が「最大値の電流」と読むならば，逆に，電流最大値でないと磁場エネルギーが蓄積されないようにもとられかねません．

>電流はどこまで上昇するのでしょうか？ 電源をステップ(無限時間)じゃなく，パルス(有限幅)にすればよい話ですね．(コンデンサーのみだと，I=∞が発生しますけど） (また，抵抗Rありのステップ電圧印加で最大値の電流を問題にすると，何時になったらこの最大値に達するのか気になりますし， その間の挙動も気になってしまいます．）

せっかくエネルギーの話をしているのだから，時刻0〜Tまでのパルスにすれば，最終的な電流はIf=ET/L． 電源から投入したパワーは，P=∫EIdt=E＾2T/2L，仕事W=PT=(ET)＾2/2L． コイルに蓄積されたエネルギーはU=LIf＾2/2=(ET)＾2/2L． (ちなみにコイルに蓄積されたエネルギーも力学対応m→L,v→Iが成立．） つまり，W=Uですから，電源からの投入エネルギーがロスなくコイルエネルギーに転化するという保存関係が示せます． 抵抗があるとこうシンプルになりません．

このようにコイルエネルギーのロスがない状態で，回路に抵抗Rを挿入(または，VRを0からRに)すると，時定数R/Lで電流Ifが減衰します．抵抗Rで消費されるエネルギーは一定であるため，抵抗Rが大きいほど，R両端の電圧が高くなることが直に判ります． (短時間で一定量消費するため，その分電圧が上がる)

>「何を指して逆起電力」とは正に，コイルの発生する起電力の事です． 電流を注入するときにコイルが起電力を生み出すようにも受け取られます． この起電力を取り出すことはできるのでしょうか？(取り出せない電力を電力と呼ぶなら違和感を感じます．)

ミュフ猫 さんのレス (2009/07/28(Tue) 17:19)

No.24867 の記事を修正しました． 何を勘違いしてたのか，大ボケかましてました．

大変，申し訳ありません．m(_ _)m

ASA さんのレス (2009/07/28(Tue) 19:31)

No.24902の訂正，補足をしておきます． １．パワーP(仕事)は，P=∫[0,T]E*I(t)dtでOK．ちなみにI(t)=Et/L ２．仕事率(ワット数);W=E*I． 平均仕事率;AW=E*If/2， トータル仕事;P=AW*T=E*If*T/2 ちなみに，If=ET/L． 元は，１と２がごっちゃになってます．

mNeji さんのレス (2009/07/28(Tue) 20:36)

ASAさんのNo.24902の記事に対してコメントします．

＞>ステップ応答の仕組みを理解した方が，明快なイメージを組上げられると思うからです． ＞これはさほど問題視してません．

私と意見の違うのは了解しました．それならご自分の説明を解り易くすれば，それによって jediさんの理解が高まると思います．私は，自分の信念に基づいて，説明にトライしているだけです．ただし，このような説明は初めてなのでドタバタしていますし，gediさんの疑問点と合致してるかどうかは不明です．

＞ミュフ猫 さんは，内部抵抗の存在が電磁誘導現象で必要不可欠と考えているようですが，mNejiさんも同様に必要不可欠と考えておられるのでしょうか？ ＞もし，不必要と考えているなら，省いて説明した方が初学者に本質が判りやすい説明になると考えます．

ミュフ猫さんの観点は判りませんが，私の考えでは，純粋にコイルだけとするのは，逆に混乱し易いと思います．電流が無限大になるような設定は不自然だし，イメージし難いとおもいます．例えば，コイルの逆起電力がある為に，抵抗に加わる電位差が低下する事が明確になります．

回路の動作を理解するという点で考えれば，複素インピーダンスを持ち込んで，通常の抵抗の論議と類似して考えた方が効率もいいですし，結論も速いです．

でも，今回の問題のように，「電源の起電力」と「コイルの逆起電力」とを考えていくには，考え易い微分方程式とその解の特徴，電場や磁場との関係を明示的に示す方が優先すると思います．

＞例えば，誤解を受けやすい表現として ＞>電流は最大値となり，逆起電力はゼロとなっています．この電流に伴って保持される磁束によって磁場にエネルギが蓄えられていると考えられます ＞「この電流」が「最大値の電流」と読むならば，逆に，電流最大値でないと磁場エネルギーが蓄積されないようにもとられかねません．

ここら辺は，私も初めて書いているので，表現の修正や工夫が必要と思いますので，ご意見を参考させて戴きます．

＞>電流はどこまで上昇するのでしょうか？ ＞電源をステップ(無限時間)じゃなく，パルス(有限幅)にすればよい話ですね．(コンデンサーのみだと，I=∞が発生しますけど） ＞(また，抵抗Rありのステップ電圧印加で最大値の電流を問題にすると，何時になったらこの最大値に達するのか気になりますし， ＞その間の挙動も気になってしまいます．）

パルス(有限幅)のアイデアは No.24887に示していますが，それは観点がすこし違います．

自分の感触では，ステップ応答の解とその概略図を出して説明できれば，もう少し解り易くなると感じています．なお，指数関数的な変化は色々な問題で出て来るので，時定数の概念があれば，そんなに難しくないかと思います．

＞せっかくエネルギーの話をしているのだから，時刻0〜Tまでのパルスにすれば，最終的な電流はIf=ET/L（以下略）

力学的類推とかパルスなどの表現は不得意なので，宜しくお願いします．

mNeji さんのレス (2009/07/28(Tue) 23:17)

ミュフ猫さん，

修正文を拝見しましたが，まだ理解出来ません．やはり，別スレッドに式を含めて説明下さるのがベストだと思います．

問題は，電磁誘導に相当する部分と，抵抗成分に当る部分とを，定量的にお示しになる必要が有るのでしょうね．

mNeji さんのレス (2009/07/29(Wed) 02:34)

jediさん，

数研出版の物理II (平成19年発行)がようやく出て来ました．

関連しそうな部分の目次； <pre> 第４章 電磁誘導と電磁波 1 電磁誘導の法則 p134 2 交流の発生 p140 3 インダクタンス p144 A 自己誘導p144 B コイルの自己インダクタンス p144 C コイルにたくわえられるエネルギーp145 D 相互誘導p145 （以下略） </pre>

お持ちの版と近そうですか？

自分の想定と結構似た実験構成図で説明していそうなので，もし類似性が高ければラキーです．

jedi さんのレス (2009/07/30(Thu) 00:39)

間が空いてしまい，すいません．

教科書ですが，ペイジが微妙に異なりますが， おそらく内容はほぼ同じであるかと思います．

教科書では，コイルに加わる交流電圧と コイルの自己誘導起電力が釣り合うということは記載されていませんね．

直流をもとにイメージしてみると， いけそうな(本当に微妙で，ふわふわしてる感じですが…)気がしてきました． もう少し詰めてみます．

と言っても，やはり物理だけをやるわけにはいきませんので， 暇があるときということになりますね． 以前mNejiさんが仰ったように， おそらく大学に行けばほとんど物理ばかりになるでしょうから(工学部志望です)， 高校の今にしかできない，例えば古典，世界史，等にも力を入れていきたいのです．

話が脱線しますが， 大学に入ったら，引き続き古典，新たに倫理，外国語(ポーランド語に興味があります)等も学んでみたいと思っています． 今の何でも学べる時期を大切にしないといけませんね． このことに早く気が付けてよかったです．

さらに脱線しますが， jediというのはまさしくジェダイでその由来はもちろん言うまでもないですかね(？) 私は劇中のライトセーバーというのに大変強い憧れを抱いておりまして， いつか作ってみたいと思うわけです．(レプリカ，本物問わず)

今は苦しい時期ですが，ここを乗り越えたときの希望を抱き， 日々頑張っていきたいと思っています．

話が脱線してしまい，失礼いたしました． それでは．

mNeji さんのレス (2009/07/30(Thu) 06:41)

＞おそらく内容はほぼ同じであるかと思います．

これは有難い事ですね．いま，この本を拝見していますが，「第３章電流と磁場」盛りだくさんのテーマがぎっしり入っていて，驚愕しています．

で，自分の考え方，マクスウェル方程式から自己誘導を説明する方法を再確認した所，「符号が合わない」のに気が付き，慌てています．ですから，私の論議はしばらく，保留させて頂きます．

＞教科書では，コイルに加わる交流電圧と ＞コイルの自己誘導起電力が釣り合うということは記載されていませんね．

「交流」に付いては，p148以降に

<pre> 第４章 電磁誘導と電磁波 1 電磁誘導の法則 p134 2 交流の発生 p140 3 インダクタンス p144 4 交流回路p148 A コイルのリアクタンスp148 B コイルに流れる電流 p149 C コンデンサーのリアクタンス p150 D コンデンサーに流れる電流 p151 E リアクタンスと交流の周波数 p152 F コンデンサー・コイルで消費するエネルギー p153 G 共振回路 p154 H 振動回路 p155 </pre>

と結構丁寧に説明が在る様ですね．

この「A コイルのリアクタンス」，p148のでは，明確に ・「直流電源，コイル，抵抗(電球)」の図・写真と， ・「交流電源，コイル，抵抗(電球)」の図・写真とが， 並列に示されているのは，良心的な説明と感じました．

『電球の明るさの違いで「直流」と「交流」との違いの説明』は，舌足らずの感がありますが，誘導起電力の振る舞いを定性的に示すもので，面白いですね．

＞暇があるときということになりますね． ＞以前mNejiさんが仰ったように， ＞おそらく大学に行けばほとんど物理ばかりになるでしょうから(工学部志望です)， ＞高校の今にしかできない，例えば古典，世界史，等にも力を入れていきたいのです．

あと40年位すると，強く実感するでしょう．

＞大学に入ったら，引き続き古典，新たに倫理，外国語(ポーランド語に興味があります)等も学んでみたいと思っています． ＞今の何でも学べる時期を大切にしないといけませんね． ＞このことに早く気が付けてよかったです．

私は，歳なので「尊厳死」の分野を検討しています．この分野は医学で十分に論じられていると思っていましたが，医学／生理学／生化学／心理学／看護学／宗教／倫理教育／哲学／経済学 などの総合的なテーマであるにも関わらず，各論が先行していて，総論が見えない感じを受けます．物理の側面から眺められないかと思うこの頃です．

私は語学の落ちこぼれなのですが，歳をてってから不思議と歌曲に興味が涌き，ドイツ語やスウェーデン語，ブラジル・ポルトガル語などに惹かれています．たとえ落ちこぼれでも，若い頃にならったドイツ語は，解り易いのに今更ながら驚きます(苦笑)．きっと，英語〜ドイツ語〜ポーランド語〜ロシア語，といった連鎖が在りそうですよね．

その意味で，若い頃に間口を広げておくと，将来，思わぬところで連鎖反応を起こせるのでしょうね．

＞私は劇中のライトセーバーというのに大変強い憧れを抱いておりまして， ＞いつか作ってみたいと思うわけです．(レプリカ，本物問わず)

この手の話には疎いのですが，趣味も大事だと...．要は，一人の人(ヒト)として，バランス良く活動する事がいいらしいですよ．

熱帯夜の毎日ですが，高校最後の夏ですからバランス良く頑張ってください．

mNeji さんのレス (2009/07/30(Thu) 21:38)

jediさん，

一応，ファラデイの誘導の法則，アンペールの法則を合わせて，回路中のコイルの動作を式によって表現できることを確認しました．また，教科書に沿って定性的に説明も出来ると思われます．

ついては，時間が取れたら何時でもお相手します．

jedi さんのレス (2009/07/31(Fri) 18:00)

mNejiさん，

是非ともお願いしたいです．

自分は，直流電源でいきなり電源電圧を変える場合も検討してみましたが， やはり電源電圧と自己誘導起電力が釣り合う瞬間は電流が0になるようです．

説明お待ちしております．

mNeji さんのレス (2009/07/31(Fri) 21:48)

jediさん，

＞自分は，直流電源でいきなり電源電圧を変える場合も検討してみましたが， ＞やはり電源電圧と自己誘導起電力が釣り合う瞬間は電流が0になるようです．

この「電源電圧と自己誘導起電力が釣り合う瞬間は電流が0」は一瞬の話ですがあっています．ただ，直流電源での振る舞いを考える時には抵抗成分を取り入れていた方がイメージし易いです．

いま，説明を準備始めたのですが，図の説明に時間が掛かりそうです．しばしお待ち下さい．

mNeji さんのレス (2009/08/01(Sat) 00:38)

jediさん，言葉が多くて解り難いかも知れませんが，初めての説明なので「判らん点」をご指摘ください．適宜修正します．

回路の説明の前に「ファラデイの誘導の法則」を見直しておきます．

教科書でいえば，第４章 電磁誘導と電磁波， 1 電磁誘導の法則 p134の， ・A電磁誘導 p134 ・Bレンツの法則 p135 ・Cファラデーの電磁誘導の法則 p135 のなかで，p136にある「図69誘導電力とその正負」が解り易いと思います．

リング状のコイルに下から上に磁束密度が時間的に増加した場合，その磁束密度の方向に右ネジを合わせた時に，コイルに発生する誘導起電力Vの方向は「磁束密度の増加する方向に右ネジを合わせて，その右ネジを進む回転方向の逆向き」で，その大きさはコイルを貫く磁束の時間微分に比例すると書かれています．

此れに対応するマクスウェルの方程式は；

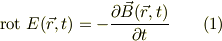
です．この式はまだ判らなくて善いのですが，これを言葉にすると；<pre> ある所(今の倍，コイルの中心部分の近くの点 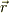)で，時刻tでの「電場の回転(rotation)」は， その点，その時刻の「磁束密度の時間についての(偏)微分」に等しい </pre> なので，何となく雰囲気が判りませんかね(笑)．

この場合， ・コイルを固定しておいて磁石を近づけたり，遠ざけたりしても， ・磁石を固定して，コイルを近づけたり，遠ざけたりしても， どちらも有りな訳です．

さらに重要なのは，コイルが無くなって仮想的な閉回路を考えて，そこに磁束密度の変化を起こすと，電場の回転を生じるということです．

そこで，コイルを考えて電流を流す場合を想像してください．これに付いては，教科書の，第３章 電流と磁場， ２ 電流がつくる磁場 p119の， ・B円形電流がつくる磁場 p120 図52 円形電流が作る磁場

によって明らかですね．この図では，電流の方向に右ネジの方向に磁場が発生する事(エルステッドの実験)から，コイルの下から上に向かって磁場(磁束密度)が出来ることを示しています．

そこで，先に示した図69のように，磁束密度の時間変化を作るには，「磁束密度が増加する方向に右ネジを置いたときに，右ネジの前進に対応した回転方向に電流を時間的に増加させる」と考えられます．その時に，回転電場は電流の増加の向きの逆方向を向く事になります．

結局，コイルの自己誘導起電力は，自らに流された電流増加に伴って発生する磁束密度の時間変化が生みだす誘導起電力であり，印可された電流の逆方向を向いているという意味で「逆」起電力と呼ばれる訳です．

＃式上のイメージでは；

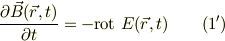
＃言葉で言い直すと，磁束密度の時間変化の方向に「左ネジ」を合わせた時に，その進行にむけて回転する方向に回転電場が生じる．

従って，回路中のコイルでは，電流が流れ込む方向に向いた電池に取り替えても良い訳です．その電池の起電力 は

jedi さんのレス (2009/08/03(Mon) 17:32)

遅れてしまい申し訳ないです． 詳しい説明をしていただいてありがとうございます．それなのに何ですが， "私が疑問に思っている点"と"mNejiさんが考えている，私が疑問に思っている点"がずれているような…．

私が疑問に思っている点は，まさに一番最初に書いたことです．

例えば，交流電源V1=Vsinωt，V2=-Vsinωtを繋いだ回路があるとします． この回路では起電力の和が0で電流は流れませんが， V2の代わりにコイルを繋ぐと起電力の和は0なのに電流が流れる…． これが掴めないのです．

非常に親切に詳しい説明をしていただいたというのに， 偉そうにこんなことを言って本当に申し訳ないです．

mNeji さんのレス (2009/08/03(Mon) 17:37)

＞私が疑問に思っている点は，まさに一番最初に書いたことです．

この場合，どんな回路を想定していますか？

恐らく，この点がはっきりすれば，jediさんの疑問を晴らせるかと推察しますよ．

mNeji さんのレス (2009/08/03(Mon) 19:59)

すこし回路の話というより，物理の法則の表現と解法の関係を考えます．

例えば，ニュートンの力学で，第一法則から第三法則まであって，そこから運動方程式が導かれます．一度，運動法則が決まれば，ここの運動は純粋に微分方程式によって記述される運動方程式を解く事になります．勿論，解けた解を，運動法則の観点から吟味したり，ある種の一般的な法則，例えば「運動エネルギ」「位置のエネルギ」「エネルギの保存」「運動量」，「運動量の保存」，「角運動量」「角運動量の保存」と発展していきます．

電磁気学は，力学よりも基礎法則が入り組んでいますし，真空中の場合と，物質中での場合と，さらに複雑で，私は「物質中での電磁気学」が苦手なくらいです．

でも，今回の回路の方程式は，歴史的にも正当性が確認され，基礎法則から導く事が可能な訳です．ですから，考える状況を回路の微分方程式で与えられたら，その式を解いてから検討するだけでしょう．解かないで方程式の外形からあまり見解を引き出すのは如何とおもいます．

その意味からすると，高校の教科書は，微分方程式も明示しないで，定性的な解だけをどんどん示して進んでいるのですから，私には理解出来る者ではありません．

Yokkun さんのレス (2009/08/03(Mon) 21:19)

>V2の代わりにコイルを繋ぐと起電力の和は0なのに電流が流れる…．

また的外れでしたらごめんなさい． 電気抵抗を考えていないからではないでしょうか？ 交流電源が逆むきについていても抵抗がなければ電流が流れておかしくないわけです． 力がつりあっていても等速直線運動は持続しますよね？ おっと直線ではなかった！螺旋？

ひょっとしてミュフ猫さんあたりが同じことを言っていたような・・・． やっとミュフ猫さんの理屈が読めました．＾＾；

jediさん，上の後半はともかくとして，直感的には慣性の法則ですかね．

ミュフ猫 さんのレス (2009/08/03(Mon) 22:52)

ありがとう！（谷村新司風にｗ）

MXK さんのレス (2009/08/04(Tue) 00:14)

>例えば，交流電源V1=Vsinωt，V2=-Vsinωtを繋いだ回路があるとします． >この回路では起電力の和が0で電流は流れませんが， >V2の代わりにコイルを繋ぐと起電力の和は0なのに電流が流れる…． >これが掴めないのです．

ここ間違ってます．

同じ起電力の電源を並列につないだ場合，電流は不定です． 電流を決める仕組みも式もないので，流れるとも流れないとも 言えません．ここを理解できれば，すっきりするかもしれません． よく考えてみてください．

電源は電流に無関係に起電力が一定．その他の素子は，電流（またはその変化， またはその積分，あるいはそれらの組み合わせ）と 起電力（両端の電位差）が拘束されている，ということがポイントです．

mNeji さんのレス (2009/08/04(Tue) 02:46)

jediさん，

ええと，話が込み入って来ている様なので，微分方程式の解法を進めます．

１階の定数係数常微分方程式で，t=0までは，電流，磁場，電源が全てゼロで，t=0以後に電源が入るという状況ですので，高校の数学の範囲で対応出来ると思われます．

以下では，一度「微分方程式」が与えられると，電源が直流電源であろうが交流電源であろうが，微分方程式を解くと言う意味では同じであることを感じ取って頂きたくて書かせていただきました．べつに，今の段階で理解する必要はないと思います．興味があれば，数学の微分方程式を見る方が良いでしょう．若しくは，先生に助けてもらうのも一法かと...．

でも，直流電源では時間応答を追う立場ですが，交流では定常解を眺める立場と違います．自分の経験では，この差が明確に書かれていないので，悩んだものです．

＃最近，常備分方程式に凝っているので， ＃どちらかと言うと，自分の頭の整理をかねてノートにしたようなものです． ＃早めに，本来の勉学に戻られます様に．

〜〜〜〜〜〜〜

微分方程式

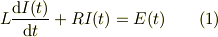
境界条件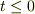， に対して

この為に，同次解(自由解)はなく，非同次解(強制解)だけを考えれば良い．

同次解は時定数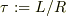， として 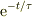となることから，非同次解は定数変化法で求められる；

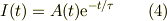
これを(1)に代入すると，

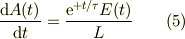
ここで，式(4)で初期条件 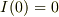を満たす為に 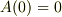に留意すると，式(5)積分より

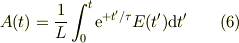
となる．

ここまでは，電源の波形は任意だったのですが，jediさんの興味がある「交流電源での振る舞い」に限定します．

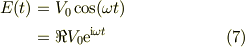
式(7)を式(6)に適用し

式(4)に代入して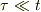， とすると，交流成分の定常解を得る事が出来る；

ここで，複素インピーダンス 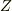を

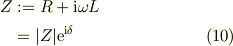
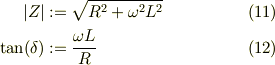
従って，電流の定常解，式(9)は

コイルに発生する誘導電圧

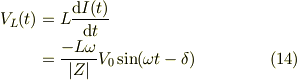
一応，コイルだけの負荷の場合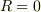， ，式(10,11,12)より

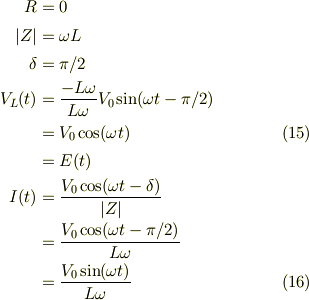
とコイルの誘導電圧が電源電圧に等しく対抗しているのが判る．でも，電流がゼロにバランスするのではない．これは，電源電圧が交流として変動しているのに，コイルの誘導電圧が常に追従してバランスしている為です．

この時に，コイルの消費する消費電力の時間平均を考えると，交流の周期 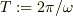とすると，

とゼロになる事です．言い換えれば，内部抵抗の無い理想的なコイルでは電力を消費しません．もう少し詳しく言えば，電流が磁場を生成し，その磁場エネルギに変換し，電流の大きさ・方向が変わるのに伴い磁場エネルギが周期的に変動して，電源とエネルギをピンポンのように交換するだけなのです．

＃なお，コイルでの電力消費が無い事は，抵抗Rがある一般の式(13)(14)でも同じである事は容易に理解出来ますね．勿論，この時にでも抵抗での電力消費は起こります．ジュール発熱は直流でも交流でも起こるという事です．

ASA さんのレス (2009/08/04(Tue) 08:33)

mNejiさん

計算はいいのですが， >これは，直流電源では釣り合いが生じれば電流がゼロになるが，交流電源の場合，電源電圧が交流として変動しているのに，コイルの誘導電圧が常に追従してバランスしている為です．

この説明は，間違いです．

直流電源でも，E=L(dI/dt)というつりあいの式は成立していて，コイルの誘導電圧が常に追従してバランスしています．

以前にも示しましたが，直流電源では，I=Et/Lという時間に比例した電流が流れます．

mNeji さんのレス (2009/08/04(Tue) 09:54)

ASAさん，

直流電源の部分は不正確であり，削除しました．別のスレッドで詳しく論じるべきと思います．なお，今現在，No.25077は検討中ですので，しばらくお待ち下さい．

豚 さんのレス (2009/08/05(Wed) 20:58)

jediさんは「逆起電力」という言葉に惑わされていませんか？ 単に「自己誘導電圧」と言い換えたらどうなんでしょう？ 抵抗に電流を流すと電流値と抵抗値に比例した電圧が発生するということと コイルに電流を流すと電流”変化率”と自己インダグタンスに比例した 電圧が発生するというのはほぼ同じことなのですが・・・

いっそ電源を「電圧源」ではなく，「電流源」で考えたらどうなのでしょう？ i(t)=Isin(ωt)なる電流源をインダグタンスＬなるコイルにつなぐと コイルにはIωLcos(ωt)という電圧が発生することは納得できるでしょうか？

そして，電圧Ｅなる電圧源に抵抗Ｒを直列につないだものは 電流Ｉ（＝Ｅ／Ｒ）なる電流源に抵抗Ｒを並列につないだものと 等価であることはよろしいでしょうか？

そして，R>>ωLとして電流源を電圧源に変換し， コイルに発生する電圧を変化させずに 電圧と抵抗を小さくしていくと考えてみては？

クロメル さんのレス (2009/08/07(Fri) 20:46)

だいたい読ませていただきました． なんだか，必要以上に複雑な話になってしまっているような気がします． コイルと電源だけをつないだ回路を考えます．

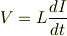
が回路方程式で，キルヒホッフの法則より， 回路を一周すると電圧変化はゼロなので， 電源とコイルには，大きさが等しく逆向きの電圧が かかります．

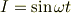
の時，

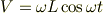
ということですよね． 二つのグラフを紙に上下に並べて描いてみて ください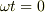． で電圧が正で最大の時，電流の増加率は 最大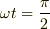． で電圧はゼロ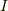， は増加をやめ， 最大値をとります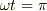． では，電圧は負で最大．この時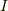， は，ゼロとなり，その減少率は最大になります．

このように続けていくと，コイルの両端の電流が変化している時， その変化率に比例した電圧を生じていると考えることができます． 電流が変化することによって，初めて逆起電力が起きるのです．

こんな感じの説明で，ニュアンスが伝わったでしょうか？

mNeji さんのレス (2009/08/08(Sat) 17:48)

クロメルさん，

＞なんだか，必要以上に複雑な話になってしまっているような気がします．

大方の皆さんはそう思っていると思います．

私が今回細かく説明したのは，自分が高校生から大学１年生の頃に感じていた疑問をもう一度確認したかったのと，高校生の数学力でも，コイルと抵抗の回路に付いては解けるだろうと考えた為です．

さて自分は中学生〜高校生にかけてアマチュア無線に凝っていました．今回の様なL，Rの交流回路どころか，L,C,Rの共振回路を計算出来ないといけないので，回路計算は出来るものの，特にコイルの(逆)起電力[ElectroMotive Force: EMF]をどう考えるか疑問に思っていたものです．

で大学では電磁気だけは人よりも一生懸命に勉強し，まずフィンマンさんの電磁気にトライしたものの歯が立たず，砂川さんの理論電磁気学に出会って納得したつもりです．ただ，交流回路の取り扱いと，直流回路の取り扱いが必ずしも統一的でない感じはしたままでした．

当時，感じたのは，直流電位のステップ応答を考えるのが，コイル・コンデンサの特性を理解するのに最適と考えていたので，今回もその立場で解説しました．その後，高校の物理IIの教科書を拝見すると，まさに同じ立場で書かれていますが，不思議と微分方程式を書かないで，電流や電圧の時間応答を図だけで説明しているので驚いてしまいました．

折角，力学で運動方程式を導入しているのに，回路では式を扱えないというのは，自分には不可思議です．

しかし，最近の掲示版の質疑応答を拝見していて，微分方程式をもう一度勉強し直す機会があり，線形n次定数係数微分方程式は因数分解出来て，線形1次定数係数微分方程式が解ける限り，通常の回路の方程式ならば，高校生さんの範疇でも解けると，確信していたのです．

私の感じでは，高校の段階で「交流回路」を教えるのは止めて，直流の時間応答に限定して，丁寧に微分方程式の解き方を説明するべきと思いました．

以上が，今回の説明を作成したモーチベーションでした．あくまで，一つの考え方なのだと思います．

クロメル さんのレス (2009/08/08(Sat) 22:02)

mNejiさん， 確かに運動方程式は高校で習いますが， 回路方程式は習いませんね． 指導要領にいれれば理解が深まるでしょうにね． 浪人して予備校で習って目からウロコだったのを 覚えています．

あと，僕も制御理論を習った時， ステップ応答，ランプ応答，交流応答等 いろいろ教わって，それぞれに違いながらも， 共通の変化パターンがあったのを思い出しました． 確かに交流は一番イメージが掴みにくいと思います．

mNeji さんのレス (2009/08/08(Sat) 23:09)

クロメルさん，

＞確かに運動方程式は高校で習いますが， ＞回路方程式は習いませんね． ＞指導要領にいれれば理解が深まるでしょうにね． ＞浪人して予備校で習って目からウロコだったのを ＞覚えています．

自分のような落ちこぼれが言うのも変ですが，高校の数学と物理については，両者の連携を密にする必要があると思います．

それが駄目なら，物理数学を物理の教科書にいれて， ・ネイピア数の定義 ・オイラーの式; 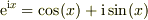・1階の微分方程式 ・２変数の全微分 程度は，どうして教えたら駄目なのかが判りません．

それに，今回，電流の関連だけを，複数の教科書で比較しましたが，何で此処まで同じなのか訝しく思えました．もっと著者によって違う解説が許されてしかるべきだと感じます．

＞あと，僕も制御理論を習った時， ＞ステップ応答，ランプ応答，交流応答等 ＞いろいろ教わって，それぞれに違いながらも， ＞共通の変化パターンがあったのを思い出しました． ＞確かに交流は一番イメージが掴みにくいと思います．

そうですか，少しホットしました．クロメルさんのシャープな視点で「共通の変化パターン」を焙り出すような解説を書いて戴けると素敵だと思いますよ．