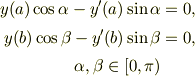Sturm-Liouville問題
Sturm-Liouville問題
間違って理系に進んだ文系人 さんの書込 (2009/07/21(Tue) 17:47)
はじめまして.次のSturm-Liouville問題を解け 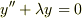 条件として
条件として 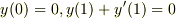 という問題なんですが....まず何を求めたらいいのですか?それとどうやって解けばいいのか教えてください.できれば実際に詳しく解いてください.
意地悪せずに親切に教えてください.
という問題なんですが....まず何を求めたらいいのですか?それとどうやって解けばいいのか教えてください.できれば実際に詳しく解いてください.
意地悪せずに親切に教えてください.
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/21(Tue) 18:44)
残念ながら,微分方程式の固有値問題を初歩から詳しく親切に教える時間も体力も気力も能力もありません.
それに,「ここは問題の答えを教えるサイトではありません」.自分で勉強する気がない人は別の場所に行った方がよいかも.
ともかく,まず,  を正のパラメータとみて,
を正のパラメータとみて, 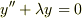 の一般解を求めてください.
の一般解を求めてください.
分からないなら 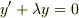 の一般解を求めてください.
の一般解を求めてください.
さらに分からないなら, 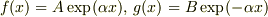 (
( 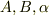 定数)と与えられたとき,
定数)と与えられたとき, 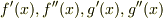 を
を 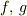 で表してください.
で表してください.
Re: Sturm-Liouville問題
mNeji さんのレス (2009/07/22(Wed) 12:30)
間違って理系に進んだ文系人さん,はじめまして.
ハンドル名の割には難しい方向から勉強されている様ですね.私は数学が苦手だったのですが,最近,微分方程式を再度勉強しようとしています.その一環で,市民図書館で関連しそうな図書を検索しては眺める(まだ勉強する手前)段階です.そのなかに「微分方程式と固有関数展開」という図書があります.
そのまえがきの先頭部分を引用させて戴きます; 〜〜〜〜 本書は Sturm-Liouville 型と呼ばれる 2階常微分作用素の固有値問題をテーマとしており,通常の固有関数展開の話に始まって,連続スペクトルが現れる場合の一般固有関数展開定理や固有関数の詳しい性質を解説したものである.(以下略) 〜〜〜〜
私には難しすぎて判りませんが,図書館で眺めてみられたら如何でしょうか.
資料情報を下記に示します.
書名 岩波講座現代数学の基礎6 出版社 東京岩波書店 出版年月 1998.3 価格 1750円 ページ数 218p 大きさ 21cm 各巻書名 微分方程式と固有関数展開小谷真一著俣野博著 ISBN 4-00-010644-9
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/22(Wed) 13:20)
mNejiさん,さすがに「岩波講座」は厳しいと思いますよ.
ここで出てくる問題は量子力学の箱形ポテンシャル問題をやったことがある人なら,ものの10分でできる初等的な問題です.
でも,スレ主さんは,おそらく,微分方程式や複素数の取り扱いを知らないので,そこから始めるのは結構大変ですね.
Re: Sturm-Liouville問題
mNeji さんのレス (2009/07/22(Wed) 13:37)
toorisugari no Hiroさん,行き過ぎでしょうかね.
でも「次のSturm-Liouville問題を解け」という書き出しがあるというのは特殊な状況のご質問だと感じたのです.
では,同時にお借りした本ですが,
書名 常微分方程式 著者名 高崎金久著斎藤秀司編集戸瀬信之編集三松佳彦編集 出版社 東京日本評論社 出版年月 2006.12 価格 2500円 ページ数 7,264p 大きさ 22cm シリーズ名 SERIES●理科系の数学入門4 ISBN 4-535-60415-0
これは如何でしょうか?ざっと拝見したところ,なかなかバランスが良いかと感じました.私は,岩波の「理工系の基礎数学」が好きなのですが,自分の所の市民図書館にはこの岩波のシリーズがないので,この「SERIES●理科系の数学入門」を参考にしようかと思いました.
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/22(Wed) 14:13)
> 行き過ぎでしょうかね.
「岩波講座」ではわたしも沈没してしまいます.:-)
たぶん,微分の初歩(鎖則や積の微分,三角関数や指数関数や対数関数の微分),積分の初歩,テーラー展開やオイラーの公式や双曲関数といった,微分方程式を理解するための「前提」から記述している微分方程式の本が必要だと思います.
> でも「次のSturm-Liouville問題を解け」という書き出しがあるというのは特殊な状況のご質問だと感じたのです.
この問題微妙なんですよね.単振動の方程式の一般解を「知っている学生」が,
「 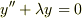 ,境界条件
,境界条件 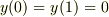 を満たす
を満たす  を求めよ.」
という問題の解法の説明を受けたとしたら,今回の問題も,三角関数を含む条件式までなら,直ぐに求めることができてしまいます.つまり,Sturm-Liouville問題としてはそう高度な問題ではないです.
を求めよ.」
という問題の解法の説明を受けたとしたら,今回の問題も,三角関数を含む条件式までなら,直ぐに求めることができてしまいます.つまり,Sturm-Liouville問題としてはそう高度な問題ではないです.
スレ主さんは前提段階で躓いておられると思います.
Re: Sturm-Liouville問題
mNeji さんのレス (2009/07/22(Wed) 15:42)
>「岩波講座」ではわたしも沈没してしまいます.:-)
なるほど.むしろ市民図書館にこの本があるのが不思議だと思って,丁寧に拝見すると「寄贈」でした.おかげで,一生見る事の無い本を拝見する事ができました.
>単振動の方程式の一般解を「知っている学生」が,「 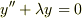 ,境界条件
,境界条件 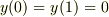 を満たす
を満たす  を求めよ.」(以下,省略)
を求めよ.」(以下,省略)
そうですね,少し前の自分でしたら,仰る通りかも知れません.
だから若い頃には,「Sturm-Liouville 問題」といわれるとなんで廻りくどい問題設定をするのかと感じていて,理解の外側にいたようです.
自分も,微分方程式の再度の勉強の一環に入れさせて頂きます.横から,失礼しました.
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/22(Wed) 16:23)
話のついでとヒント代わりに,一番簡単なSturm-Liouville問題の例
「 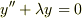 ,および,境界条件
,および,境界条件 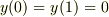 を満たす非自明な
を満たす非自明な  が存在するような
が存在するような  を求めよ.」
の解法を書いておきます.
を求めよ.」
の解法を書いておきます.
上の方程式および境界条件は 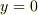 を明らかに解にもつ.しかし,この解は(当たり前すぎて)意味がない.このような自明な解
を明らかに解にもつ.しかし,この解は(当たり前すぎて)意味がない.このような自明な解 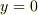 以外の解が存在するような
以外の解が存在するような  を求める.
を求める.
 を正と仮定する.
を正と仮定する.
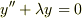 の一般解は
の一般解は 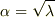 とおいて,
とおいて,
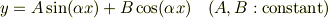
となる.
境界条件 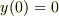 より,
より,  .
境界条件
.
境界条件 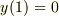 に修正した一般解
に修正した一般解 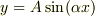 を代入すると,
を代入すると,
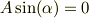
となる.
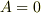 では自明な解
では自明な解 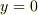 となってしまうので,自明ではない解が存在するためには,条件式
となってしまうので,自明ではない解が存在するためには,条件式
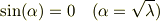
を満たさなければいけない.これを満たす  が,非自明な解が存在するためのパラメータ,すなわち,固有値である.
が,非自明な解が存在するためのパラメータ,すなわち,固有値である.
一般に  の満たす条件式(代数方程式)は解析的に解けないことが多いので,
の満たす条件式(代数方程式)は解析的に解けないことが多いので,  の代数方程式を出せば,題意を満たしたことになる.
の代数方程式を出せば,題意を満たしたことになる.
しかし,本問題の代数方程式は解くことが可能で,上の式の解,すなわち,固有値は 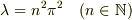 となる.
(
となる.
( 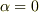 つまり
つまり 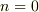 では自明な解
では自明な解 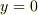 となるので除去される.)
また,各固有値
となるので除去される.)
また,各固有値  に対応する非自明な解,すなわち,固有関数は
に対応する非自明な解,すなわち,固有関数は
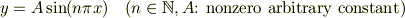
である.
なお,  が負または0の場合,
が負または0の場合,
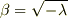 とおいて,一般解
とおいて,一般解
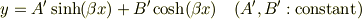
に対して同様の計算をすると
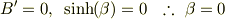
となり, 自明な解しか存在しないことが示される.
Re: Sturm-Liouville問題
間違って理系に進んだ文系人 さんのレス (2009/07/22(Wed) 18:03)
ここで出てくる問題は量子力学の箱形ポテンシャル問題をやったことがある人なら,ものの10分でできる初等的な問題です.なら解いてください.いじわるでしょ?それ.
話のついでとヒント代わりに. ヒント出すぐらいの余力あるなら解いてください.どうしてそういじわるなんでしょうね.性格曲がってませんか?
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/22(Wed) 18:35)
あああ,終わったな. いじわるで性格が曲がった私は身を引きます.
Re: Sturm-Liouville問題
mNeji さんのレス (2009/07/22(Wed) 20:06)
間違って理系に進んだ文系人さん,
No.24809の「ヒント」は,「いじわるで性格が曲がった」と語られるtoorisugari no Hiroさんの解説のなかでは,とても丁寧なご説明だと思います.
私の場合では,物理の問題の場合に計算で躓いていると感じたときは,出来るだけ数式の流れを書く様にしていますが,こと数学の計算がメインな場合,解説を控える様にしています.それは,「答えを知ったらそれで終わり」というケースが多く,回答しても無常観を感じてしまうからです.
私自身,物理にとって数学は道具だと割り切っていたのですが,こちらのサイトで,toorisugari no Hiroさんの解説を拝見している内に,数学もバックグランドを理解しないと使いこなせないと実感するようになってきました.
注意するべきは,toorisugari no Hiroさんの解説の真意は掴み辛く(とてもクールな解釈の為に),何度も見たり,時間を置いて見直しているうちに気付くことも在りますよ,中には今だ謎のままだったりしますが時と共に理解出来ると願っています.(体験者談)
Re: Sturm-Liouville問題
anon さんのレス (2009/07/23(Thu) 16:26)
>> 24811
>> >> ここで出てくる問題は量子力学の箱形ポテンシャル問題をやったことが >> >> ある人なら,ものの10分でできる初等的な問題です. >> なら解いてください.いじわるでしょ?それ. まあ落ち着いて 24804 を読み返してみてください. この問題が初等的だといったのは,mNejiさんが薦めた書籍は少しレベルが高いので, 初等的な問題で躓いているスレ主さんには合わないでしょうという話ですよ. スレ主さんに向かって,「こんなの簡単ですよー」的に意地悪で言っているわけではないですよね.
>> >> 話のついでとヒント代わりに. >> ヒント出すぐらいの余力あるなら解いてください. >> どうしてそういじわるなんでしょうね.性格曲がってませんか? 数学の問題というのは,特定の問題の計算を追うだけでは身に付かないのが常です. ヒントを受けて,まず自分で考えてみることからはじめないと. どこの学校の教室でもそういうふうにやられていますよね. それが一番身に付くのですから,スレ主さんのためを思ってのことでしょう. 他人の善意を意地悪だなんていうものではないですよ.
Re: Sturm-Liouville問題
間違って理系に進んだ文系人 さんのレス (2009/07/29(Wed) 12:26)
ヒントを受けて,まず自分で考えてみることからはじめないと. どこの学校の教室でもそういうふうにやられていますよね. それが一番身に付くのですから,スレ主さんのためを思ってのことでしょう. 他人の善意を意地悪だなんていうものではないですよ. ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ 嘘だなwただ知識を見せびらかしたいだけの言い訳に見える.解答を教えてもらって考える方が身に付くと思いますけど?それに本当に善意があるなら教えてくださいよ!?別に数学の力なんていりませんからwその場しのぎでいいんです. じゃあ聞きますけど,街で道に迷ってる人がいて道を聞いてきたとき,あなたは目的地への行き方を知っていてもあえて行き方を教えず,自分で調べた方がこの辺の地理が分かると言い,道を教えませんか?そんなの意地悪にほかならないとおもいますけど?
Re: Sturm-Liouville問題
mNeji さんのレス (2009/07/29(Wed) 12:58)
逆にお聴きしたいのは,なぜ此処のサイトで回答を得たいのでしょうか?
今は,何処かの学校で,授業を受け・その中での例題なり設問を考えているといった状況ですよね.当然の事として,学生として授業を受けている対価として授業料を払っていると思います.従って,授業で理解出来ない所は,担当教官にお尋ねになるのが一番の方法と思います.そのような質問があれば,詳しく説明をしたり,授業内容を工夫したり,等の改善があると思われますが?
また,他のサイトでは,「質問と回答」に特化した所も在る様です.その意味では,質問先が間違っていると感じます.
このサイトでは,「本とか講義で受けた説明が理解出来ない」といった場合に,観点を変えた説明とか,欠落している考えの指摘とかをすることを目指していると思っています.
Re: Sturm-Liouville問題
ASA さんのレス (2009/07/29(Wed) 13:24)
mNejiさん
回答の可能性がある場所全てにあたってみるというのは,戦略的に間違ってません.(スレ主は,このサイトのみに拘っていると見えないですし.) 微分方程式の解法を知っていたとしても,社会で役立つことはまずありません.役立つのは,正解のない問題に遭遇したとき,妥当な解を創出する能力です. ですから,このような戦略的アプローチを否定するのは,いかがなものかと思います.
余談ですが,λの場合分けで超越方程式を解かなければならないから,この問題は,難度が高いと思います. (しかし,世の中甘くはありません,私なら有料サービスですね.)
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/29(Wed) 23:09)
身を引いた人間ですがASAさんにご用があります.
> λの場合分けで超越方程式を解かなければならないから
?
固有値の代数方程式なら確かに漸近的解を出すぐらいしか初等的な計算はできないけど,「λの場合分けで超越方程式を解かなければならない」は理解できません.
 が正の領域に分布することを示すのは,この境界条件の場合難しくないですよ.微分方程式を解かなくても,わりと初等的に求められますね.
が正の領域に分布することを示すのは,この境界条件の場合難しくないですよ.微分方程式を解かなくても,わりと初等的に求められますね.
「λの場合分け」が別の意味だったら,堪忍.
Re: Sturm-Liouville問題
ASA さんのレス (2009/07/30(Thu) 06:42)
toorisugari no Hiroさん
λはコンプレックスですよね. >わりと初等的に求められますね. そうなんですか.初等的なやり方がわからないので教えてください.
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/30(Thu) 10:27)
誤解してました.
> λの場合分けで超越方程式を解かなければならないから,この問題は,難度が高いと思います. > λはコンプレックスですよね.
なるほど,複素数までは考えていませんでした.そういう意味では,先のヒントも複素数も場合に入れないなければいけないので大変ですね.
私は単にλが負の場合だけを考えていました. 超越方程式は出ますが,グラフをイメージすれば,初等的に解けるし.
そもそも,正の場合だけ考え他の場合は省略しても,出題の文脈からまあOKかと思います.
> 初等的なやり方がわからないので教えてください.
超越方程式といった難しい考えでなく,部分積分です.
演算子 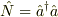 が非負の実固有値を持つことの証明と本質的には同じ考え方でできます.
が非負の実固有値を持つことの証明と本質的には同じ考え方でできます.
Sturm-Liouville問題って境界条件がやっかいだけど,方程式に含まれるのは( 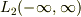 における)非負のエルミート演算子ですよね.
# ここから先は有料:-)
における)非負のエルミート演算子ですよね.
# ここから先は有料:-)
Re: Sturm-Liouville問題
ASA さんのレス (2009/07/30(Thu) 11:49)
://www.f-denshi.com/000TokiwaJPN/14bibnh/110deq.html これみると やはり,Sturm-Liouville問題とは,実固有値に限定した問題ではなく, Lu(x) = λρ(x)u(x)で表現されるスツリムリウビル型の微分方程式を与えられた境界条件(非同次でない場合も含む)で,自明でない解(固有関数)とその固有値とを求める問題だと解釈できます.
物理的な応用がいろいろあるのは,実固有値のケースですが,数学の問題なら実固有値に限定する必然性がありません.
λ^(1/2)=lnr +iθと複素数表示したとき, ちなみに,rlnr/(r^2-1)=θ/2sinθ(r^2+2rcosθ+1≠0) というようなf(r)=g(θ)の条件式を導く問題と捉えました(計算ミスあるかもしれないから要注意;符号違いはよくやる). lnr→0の極限では不定形なので,θ=-tan(θ);θ=0は自明解なので除く. θ→2πnではlnr=φとおいて,φ=-tanh(φ)(実虚の90度回転),φ=0で自明解しかもたない.等々と細かく詰めるので面倒です.
>部分積分です. 今の場合のような非同次境界条件でも初等的で単純ですか? (yもコンプレックスですよね)
Re: Sturm-Liouville問題
ASA さんのレス (2009/07/30(Thu) 15:43)
OK. エッジでの条件;y'(l)=-y(l)で異なる固有値の固有関数が直交すること, それゆえに実固有値であること,また,本ケースでλ>0を確認. 初めにこの段取りで,絞り込んでおくのも1つの方法ですな.
Re: Sturm-Liouville問題
toorisugari no Hiro さんのレス (2009/07/30(Thu) 17:10)
> 初めにこの段取りで,絞り込んでおくのも1つの方法ですな.
Sturm-Liouville問題的にはここのcheckが肝ですが, 先の問題の場合は出題者がそのようにつくって,解答者は機械的に実係数2階微分方程式を解くというパターンでしょうかね.
![-\frac{d}{dx}\left[p(x)\frac{dy}{ dx}\right]+q(x)y &=\lambda w(x)y\quad x \in (a,b), \\y(a)\cos \alpha - p(a)y^\prime (a)\sin \alpha &= 0,\\y(b)\cos \beta - p(b)y^\prime (b)\sin \beta &= 0,\\p(x)>0, q(x)>0,w(x)>0,\alpha,\beta\in [0,\pi)&](http://hooktail.maxwell.jp/bbslog/03f40c46fe1795c73b014cd6ff57e99e.png)
に従っていれば方程式にかかる演算子はエルミートになり,実固有値で考えられますし, 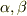 を上手に選べば正値となりますね.
を上手に選べば正値となりますね.
Re: Sturm-Liouville問題
ASA さんのレス (2009/07/30(Thu) 17:51)
確かに固有値問題になっているかチェックすることが肝ですよね.
あと,示された条件では厳しすぎるような.
直交すると実固有値が導かれるから, そこで ttp://www.f-denshi.com/000TokiwaJPN/14bibnh/110deq.html をみると判定条件がuk(x)u'j(x)−uj(x)u'k(x)}[a,b]=0なので (p(x)は,くくりだされている) {y1(a)y2'(a)−y2(a)y1'(a)}=0 ならクリアしそうです. したがって K1y(a)-K2y'(a)=0 K3y(b)-K4y'(b)=0 K;実数 あたりでは?(ということで,同次以外の境界条件チェックでもp(x)を気にしなくてよいような気がしますけど)
Re: Sturm-Liouville問題
anon さんのレス (2009/07/31(Fri) 10:46)
>> じゃあ聞きますけど, >> 街で道に迷ってる人がいて道を聞いてきたとき, >> あなたは目的地への行き方を知っていてもあえて行き方を教えず, >> 自分で調べた方がこの辺の地理が分かると言い, >> 道を教えませんか? >> そんなの意地悪にほかならないとおもいますけど?
これについてはまったく同感です. 街で道に迷っている人に,道を知っていても教えないなんて,意地悪ですよね.
ですが,間違って理系に進んだ文系人 さんがここで質問したことは, 喩(たと)えて云うなら, オリエンテーリングをやっていてポイントを見つけられない人が, 次のポイントはどこにあるのか訊いているようなものですよね. それならば, 地図や周りの様子を一緒に見比べながら, 「ほら,あそこの少しひらけたところが,地図の中のこの部分になるんじゃない?」 なんて具合にヒントを出すくらいが適切な対応で, ポイントのありかを直接教えるのはむしろよくない対応だとは思いませんか?
ですから,ここで返答してくださっているみなさんは, 街で道に迷っている人に敢えて道を教えないような意地悪を しているわけではないと思いますよ.
![-\left[y^{*}\frac{\mathrm{d}y}{\mathrm{d}x}\right]_{0}^{1}](http://hooktail.maxwell.jp/bbslog/9ab7cd2b9a44442bcbdc54c351a0dd74.png) で非負.残りの項も非負ですよね.
で非負.残りの項も非負ですよね.