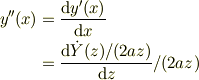ベッセル関数
ベッセル関数
E.Y さんの書込 (2009/07/20(Mon) 16:34)
はじめまして!数学ができる人には何で分からないんだと言われるかもしれませんが,次の問題教えてください. 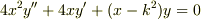 をベッセル関数
をベッセル関数 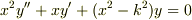 に帰着させたいのですがどうしたらいいですか...馬鹿な質問ですいません.
に帰着させたいのですがどうしたらいいですか...馬鹿な質問ですいません.
Re: ベッセル関数
mNeji さんのレス (2009/07/20(Mon) 18:13)
二つのの方程式での最後の項で, 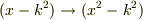 が印象的ですので,
が印象的ですので,
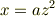
とでも変数変換してみたらどうでしょうか.
従って, 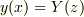 と考えるので,例えば,一次微分は
と考えるので,例えば,一次微分は
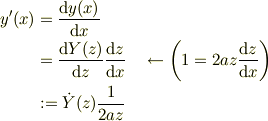
となるので,二次微分も同様に求められますね.
書き換えた方程式が望む形になるようにaを決めたら良いと思います.
Re: ベッセル関数
EY さんのレス (2009/07/21(Tue) 14:43)
分からないので...2次微分もやってもらえませんか??すいません...
Re: ベッセル関数
EY さんのレス (2009/07/21(Tue) 17:35)
そうすると 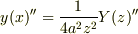 となりますよね?
でも仮に
となりますよね?
でも仮に 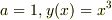 だとすると
だとすると 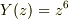 で
で
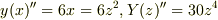 となって
となって 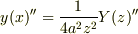 と合わなくないですか?
と合わなくないですか?
Re: ベッセル関数
mNeji さんのレス (2009/07/21(Tue) 20:20)
ええと,部分的に評価しないで,元の方程式全体を変換してください.今問題なのは,変数を変換した時に,微分方程式がどのように変わるかを考えようとしている訳ですよね.
例えば,
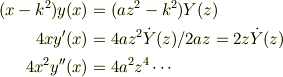
なお,
![y''(x) &= \frac{\mathrm{d}y'(x)}{\mathrm{d}x}\\&= \frac{\mathrm{d}\dot Y(z)/(2az)}{\mathrm{d}z}/(2az)\\&= \left[\ddot Y(z)/(2az)+\dot Y(z)\frac{-z^{-2}}{2a}\right]/(2az)&= \frac{\ddot Y(z)}{4a^2z^2}-\frac{\dot Y(z)}{4a^2z^3}](http://hooktail.maxwell.jp/bbslog/57d9fa5296fe5d7e7b8b3daa5442c18f.png)
でしょう.
Re: ベッセル関数
Y.E さんのレス (2009/07/21(Tue) 21:18)
>分からないので...2次微分もやってもらえませんか??すいません...
絶望的なほどに基礎が欠落しとる この程度もできないようじゃ説明したところで無理な希ガスる これが本当にできないとすると高校の数学からやり直すべき
Re: ベッセル関数
EY さんのレス (2009/07/22(Wed) 20:36)
mNejiさんありがとうございました.自分馬鹿な勘違いをしていたようです. 完璧に理解しました.
Re: ベッセル関数
mNeji さんのレス (2009/07/22(Wed) 20:59)
>自分馬鹿な勘違いをしていたようです. >完璧に理解しました.
なるべく早めに「間違えや勘違い」を沢山して,乗り越えるのが大切だと思います.