数値が合わないのです
数値が合わないのです
ひよこ さんの書込 (2009/07/18(Sat) 13:59)
はじめまして.物理勉強を始めて間もない「ひよこ」です. 演習問題を解いてみたら,解答と数値が合わなくて困っています.問題自体はシンプルなのですが,解答が数値のみで,自分のミスの場所が見つけられません.相談に乗っていただきたいです.よろしくお願いします.
(問題)厚さ0.2m 屈折率1.5 のガラス板によって,屈折した光線の経路は,平行にずれることになります.入射角が30度 の時,そのずれはいくつか?
という問題です. 平行にずれることは納得したのですが,解答を見ると,ずれが0.0425m です. この数値が合いません. 問題に指定がなかったので,私は空気中の屈折率を1.0で計算しました. 検算していただけると助かります.
Re: 数値が合わないのです
toorisugari no Hiro さんのレス (2009/07/18(Sat) 15:25)
> 数値が合わなくて困っています. > 解答を見ると,ずれが0.0425m です.この数値が合いません.
あなたの出した答えと導出過程を書いてください.
Re: 数値が合わないのです
ひよこ さんのレス (2009/07/18(Sat) 16:59)
説明不足ですいません.
私の解答方針は, 「求める平行線のずれ」と「ガラス内の光線」が直角三角形の2辺であり,ガラス内の光線は斜辺に相当する.の利用です.
ですから,ガラスの厚み0.2mと,屈折角の余弦が ![\frac{2\ \sqrt[]{2}}{3}](http://hooktail.maxwell.jp/bbslog/7d63cf803a55f5e7137b0b05118599b0.png) になることから,まずは,ガラス内の道のりを
になることから,まずは,ガラス内の道のりを ![\frac{3}{10\ \sqrt[]{2}}](http://hooktail.maxwell.jp/bbslog/af5fb1dbc2007ae13e72549a2fa4c0e5.png) と算出.
と算出.
次に,最初に述べた直角三角形のひとつの鋭角は「入射角と屈折角の差」に等しいので,この鋭角の正弦を加法定理を用いて ![\frac{2\ \sqrt[]{2}-\sqrt[]{3}}{6}](http://hooktail.maxwell.jp/bbslog/42da275f88f474aa13b43398fed029ab.png) と算出.
と算出.
最後は算出した「斜辺の道のり」と「正弦の値」をかけて,
求める長さは ![\frac{4-\sqrt[]{6}}{40}](http://hooktail.maxwell.jp/bbslog/52813061aad0a75f9016987980f99b49.png) となりました.
電卓で計算すると,約0.03876 です.
となりました.
電卓で計算すると,約0.03876 です.
検算よろしくお願いします.
Re: 数値が合わないのです
山旅人 さんのレス (2009/07/18(Sat) 20:31)
私も ひよこ さんの結果と同じ値になりました.
Re: 数値が合わないのです
ひよこ さんのレス (2009/07/18(Sat) 23:20)
山旅人さん,ありがとうございます. そうですか〜,同じになりましたか.となると,誤植の可能性が高そうですね.
ご協力ありがとうございました.
誤植?
山旅人 さんのレス (2009/07/19(Sun) 00:23)
> 誤植 いいえ! 0.03876 とすべきところを0.03867 としてしまった,これを誤植といいます.演習問題の解答は 誤答 です.
Re: 数値が合わないのです
mNeji さんのレス (2009/07/19(Sun) 00:49)
横からしつれいします.
入射角を 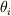 ,屈折角を
,屈折角を 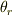 とすると,ずれ長zは,ガラスが無かった時に厚さdを通過したときの横幅と,ガラスがあった時の横幅の差ではないでしょうか?
とすると,ずれ長zは,ガラスが無かった時に厚さdを通過したときの横幅と,ガラスがあった時の横幅の差ではないでしょうか?
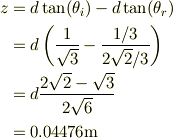
Re: 数値が合わないのです
mNeji さんのレス (2009/07/19(Sun) 19:43)
入射光がガラス無しでそのまま進行した仮想上の直線と2回屈折した後の直線との距離Lとすると,
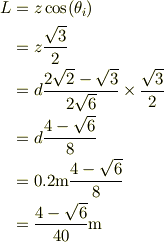
となって,一致するようです.
なお,物理の問題では,「数値と単位」は不可分なので三角関数や指数関数などの無次元の場合と長さなどのように次元を持つ量の混在する場合は「単位」を付けるようにしておくと見やすいですし,間違いも少ないと思いました.