微分方程式

微分方程式

数学見習い さんの書込 (2009/07/16(Thu) 21:22)

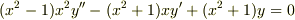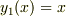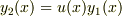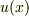常微分方程式について教えてください． (x^2-1)x^2y''-(x^2+1)xy'+(x^2+1)y=0 を定数変化法で解きたいです． そこで y_{1}(x)=x をこの微分方程式は解に持つから， y_{2}(x)=u(x)y_{1}(x) とおいて u(x) を決めようと思うのですが，実際やってみたら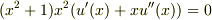， (x^2+1)x^2(u'(x)+xu''(x))=0 となってここからどうしたらいいか分かりません．よかったら教えてください．

あともう１つですが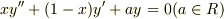， xy''+(1-x)y'+ay=0 (a \in R) をべき級数解法で解くもんだいですが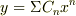， y=\Sigma C_{n}x^n とおいて代入して解いたらいいんですよね？？？

Re: 微分方程式

mNeji さんのレス (2009/07/16(Thu) 21:49)

数学見習いさん，私も最近になって常微分方程式に手を出していますが...，一寸参考意見．

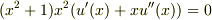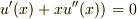＞実際やってみたら， (x^2+1)x^2(u'(x)+xu''(x))=0 となって

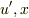素直に， u'(x)+xu''(x))=0 としてみると「 u',x 」で変数分離できませんか？

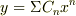＞ y=\Sigma C_{n}x^n とおいて代入して解いたらいいんですよね

これも，実際に代入してみたら，どうでしょうか？

Re: 微分方程式

数学見習い さんのレス (2009/07/16(Thu) 22:58)

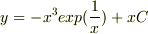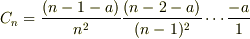上の問題はなんとか出来ました．変数分離にきがつきませんでした； ありがとうございます．いちおうですが y=-x^3exp(\frac{1}{x} )+xC であってますか？？ 下の問題なんですが，やってみたところまた手が止まってしまいました．．． すいません，，， C_{n}=\frac{(n-1-a)}{n^2} \frac{(n-2-a)}{(n-1)^2} \cdots \frac{-a}{1} となってしまったのですが，これはこれでいいのですか？？？

Re: 微分方程式

mNeji さんのレス (2009/07/17(Fri) 00:02)

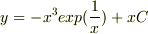＞ y=-x^3exp(\frac{1}{x} )+xC であってますか？？

ご自分で検算(基の微分方程式に代入してチェック)されて見ましたか？

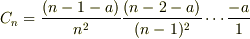
＞ C_{n}=\frac{(n-1-a)}{n^2} \frac{(n-2-a)}{(n-1)^2} \cdots \frac{-a}{1}

って，どうやってこの値が出て来たかを書かれた方が，助言が出易いとおもいますが．

Re: 微分方程式

anon さんのレス (2009/07/17(Fri) 09:13)

一番初めの問題の部分ですが，最初の(x^2-1)のところは(x^2+1)の間違いではないですか？ そうでないと，あとのところで(x^2+1)x^2(u'+xu'')=0にならないような...

Re: 微分方程式

mNeji さんのレス (2009/07/17(Fri) 12:58)

anonさん，

もしそうすると，微分方程式が簡単になりすぎませんかね．

むしろ，

(x^2-1)x^2y''-2(x^2+1)xy'+2(x^2+1)y=0

などは如何でしょうか？

Re: 微分方程式

mNeji さんのレス (2009/07/17(Fri) 20:41)

＞下の問題なんですが，やってみたところまた手が止まってしまいました．．．

この「止まった」理由はなんですか？ここは算術の論議が主でないので，単なる答え合わせなら，あまり回答を得られないと思います．

もし，この問題を解く時の考え方が腑に落ちないなど場合は，具体的に質問される事をお勧めします．

Re: 微分方程式

mNeji さんのレス (2009/07/19(Sun) 09:51)

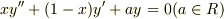＞ xy''+(1-x)y'+ay=0 (a \in R) をべき級数解法で解くもんだいですが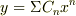， y=\Sigma C_{n}x^n とおいて代入

この方法で良いと思います．丁寧に x^n の係数をだして，その係数の和がゼロに等しいと置いて，漸化式

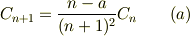
C_{n+1} = \frac{n-a}{(n+1)^2}C_n \qquad (a)

を得ます．n=0から始まって，nまで計算すると，ご呈示の式

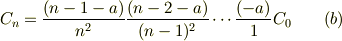
C_{n}=\frac{(n-1-a)}{n^2} \frac{(n-2-a)}{(n-1)^2} \cdots \frac{(-a)}{1} C_0\qquad (b)

が得られると思います．

問題は，この式が本当に与えられた微分方程式の解かどうかをテェックできないかと言う点です．そこで漸化式を一寸書き換えて，変形すると，大きなn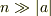（ n \gg |a| ）については，

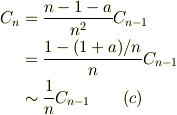
C_{n} &= \frac{n-1-a}{n^2}C_{n-1}\\&= \frac{1-(1+a)/n}{n}C_{n-1}\\&\sim \frac{1}{n}C_{n-1} \qquad (c)

であることが判ります．そこで，nの大きいほうから下に向けてこの漸化式を適用すれば，

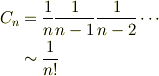
C_n &= \frac{1}{n}\frac{1}{n-1}\frac{1}{n-2}\cdots\\&\sim \frac{1}{n!}

となります．これは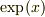， \exp(x) のテーラ展開の係数と一致します．

以上から，式(b)の式は大きなxの領域で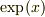， \exp(x) に漸近すると推定されます．そこで，微分方程式で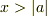， x>|a| で近似をすると，

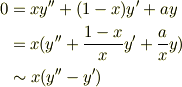
0 &= xy''+(1-x)y'+ay\\&= x(y''+\frac{1-x}{x}y'+\frac{a}{x}y)\\&\sim x(y''-y')

従って，この領域では 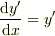\frac{\mathrm{d} y'}{\mathrm{d} x} =y' と変数分離形に近似出来るので，その積分として 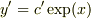y' = c'\exp(x) を得るので，最終的に

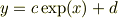
y = c\exp(x)+ d

となり，大きなxでは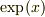， \exp(x) が解となる事が確かめられた．

〜〜〜〜 説明がダサイですが...，ご検討下さい．

Re: 微分方程式

なんとなく さんのレス (2009/07/19(Sun) 12:01)

蛇足ですが，この微分方程式はaが整数の時，ラゲール多項式となるものですので，確認されると良いでしょう．

Re: 微分方程式

mNeji さんのレス (2009/07/19(Sun) 15:23)

なんとなくさん，

＞この微分方程式はaが整数の時，ラゲール多項式となるものですので，確認されると良いでしょう．

そうなんですか，知りませんでした(汗)．「微分方程式とその解」とは，数学事典で調べるものと思い込んでいましたので...．

追伸： すると，私の論議は，「aが整数」では無い場合とさせて戴きます．