背景輻射光子と陽子の衝突
背景輻射光子と陽子の衝突
えり さんの書込 (2009/07/14(Tue) 13:59)
相対論の問題だと思い,一見すると解けそうだと思っていたのですが,実際解こうと思ったら解けないので困っています.おそらく何か基本的な知識が欠落しているのかなと思うのですが,どのように解き進めていったらいいのかわかりません. 以下に問題文を書いてみます.
「実験室系において4×10^20[eV]の全エネルギーを持つ陽子が,2.3×10^(-4)[eV]に相当するエネルギーを持つ背景輻射光子と衝突する.この際に,陽子の静止系では,光子のエネルギーはいくらになるか」
というものです.答えはだいたい100[MeV]くらいになるみたいなのですが….保存則で考えようとしても系変換と保存則をどのように考慮したらよいのかわかりません.どなたかアドバイスをいただけないでしょうか. よろしくお願いします.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/14(Tue) 14:12)
ぱっと見ただけだと,単純にドップラー効果では駄目ですか?
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/14(Tue) 19:20)
mNeji様,toorisugari no Hiro様,返信ありがとうございます.
ドップラー効果をエネルギーに適応することはできるのでしょうか? また,toorisugari no Hiro様の解き方に使っている行列は何変換というのでしょうか…
Re: 背景輻射光子と陽子の衝突
なんとなく さんのレス (2009/07/14(Tue) 19:59)
チャチャですが... 衝突の問題かと思いきや,衝突前の系変換でしたか.Hiroさんがスマートなローレンツ変換を示されていますが,以降の経過も知りたいですね. ドップラー効果との比較も見てみたいところです. このエネルギーはもう皆さん,お気づきでしょうが,GZK限界の辺りですので,散乱は本来Q.C.Dの範囲に入りそうです.どんな背景があるのか検討がつきませんが,どこへ行くのでしょう. 無責任な横レスで,失礼しましたー.
Re: 背景輻射光子と陽子の衝突
toorisugari no Hiro さんのレス (2009/07/14(Tue) 20:30)
> このエネルギーはもう皆さん,お気づきでしょうが,GZK限界の辺りですので,
なるほど,π粒子の質量が140Mevくらいですから,もう一踏ん張りで反応が起きちゃいますね(理論が正しいのなら).
> 以降の経過も知りたいですね.
いや,式が正しいのか自信ないです.(特に背景輻射の運動量を0にした辺り..)
あれが正しいのなら, 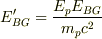 でだいたい100Mevぐらいですか.
でだいたい100Mevぐらいですか.
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/14(Tue) 21:24)
すみません,話に割り込んでしまうようで申し訳ありませんが, toorisugari no Hiro様の変換はローレンツ変換なのですか…?
私は,γやβγが行列の成分に入ったローレンツ変換を習ったのですが,同じものでしょうか?
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/14(Tue) 22:28)
この手の領域の計算は全くした事が無いので,感じだけ書いて見ます.
大雑把に,地球から見た,加速されたプロトンのエネルギについては;
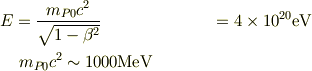
現在の地球から見た背景放射の光子のエネルギ;
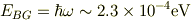
加速されたプロトンの静止系から見た光子のエネルギ(ドップラー効果);
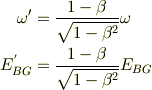
とすれば,概算は出来そうな気がするのですが....
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/15(Wed) 00:01)
どうもありがとうございます.
最後の二行はωに関するドップラー効果が成り立てば 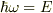 の式より,エネルギーのドップラー効果の式に書き換えることができるということを表しているのですよね?
の式より,エネルギーのドップラー効果の式に書き換えることができるということを表しているのですよね?
衝突だからといって必ずしも運動量保存を考えようといけないのですね. どうもありがとうございました.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/15(Wed) 00:16)
>最後の二行はωに関するドップラー効果が成り立てば 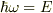 の式より,エネルギーのドップラー効果の式に書き換えることができるということを表しているのですよね?
の式より,エネルギーのドップラー効果の式に書き換えることができるということを表しているのですよね?
と推測しているだけですので.むしろ数値的に 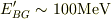 位になるかどうかですね.
位になるかどうかですね. 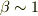 の領域の計算が上手く出来なくて,まだ判りません(泣).実際の概算をやって戴けると嬉しいです.
の領域の計算が上手く出来なくて,まだ判りません(泣).実際の概算をやって戴けると嬉しいです.
>衝突だからといって必ずしも運動量保存を考えようといけないのですね.
厳密には相対論的運動学を知らないのですが,おそらく光子さんが相手なので特別なのだと思います.とにかく光子さんは,どの座標からみても一定速度なんですよね.
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/15(Wed) 00:20)
はい,計算はちゃんとやってみます. 本当にどうもありがとうございました.
また質問させていただくかもしれませんが,そのときはよろしくお願いします.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/15(Wed) 10:38)
済みません,やはり手拍子で書き込むと間違うようですね.
例えば,h ttp://www.astr.tohoku.ac.jp/~chinone/Compton/Compton-node3.html に依ると,
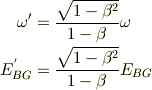
ですね.取り急ぎ,訂正させて頂きます.
ついでに,超高エネルギの概算の練習をして見ました.
プロトンに着目して;
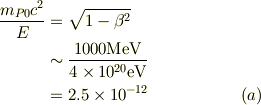
辺々自乗して,整理
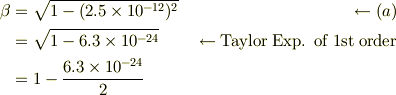
だから,
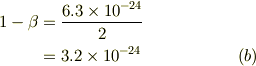
よって,
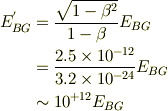
と凄まじい倍率のドップラー・シフトをするのでサブ・ミリ 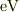 の光子でも,立派な光子としてプロトンに衝突するようになるのでしょうかね.
の光子でも,立派な光子としてプロトンに衝突するようになるのでしょうかね.
逆に,此処までプロトンを加速する機構とは何なんでしょうか?
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/15(Wed) 12:06)
さらに付け足していただいたようで,本当に助かります. 私は最初,なぜ計算がうまくいかなかったというと,陽子の質量を間違えていたため,桁が全く合わなくなっていました.
1-(とても小さい数)のときは,テーラー展開を使ったほうがいいのですね.教われば納得できるものの,未だテーラー展開に思考が飛んでいきません…まだまだ私の修行が足りませんね.
本当にどうもありがとうございました.
Re: 背景輻射光子と陽子の衝突
toorisugari no Hiro さんのレス (2009/07/15(Wed) 17:07)
> 私は,γやβγが行列の成分に入ったローレンツ変換を習ったのですが,同じものでしょうか?
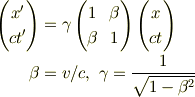
に対して 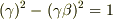 が成り立つので
が成り立つので
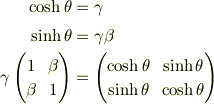
とおく事ができます.上の行列は, 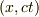 空間での光円錐
空間での光円錐 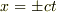 を主軸とする歪み変形に相当する行列ですが,
を主軸とする歪み変形に相当する行列ですが, 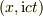 という空間では角度
という空間では角度 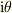 の回転行列と同じになります.
の回転行列と同じになります.
速度の合成則は双曲正接関数の加法定理に過ぎません.
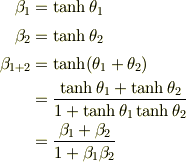
以上のことは特殊相対性理論のたいていの教科書に載っていると思います.
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/16(Thu) 15:00)
そうだったのですか….知りませんでした.
ところで,昨日先生にお話伺う機会があったので聞いてみたところ, やはり,この問題はローレンツ変換を用いて解くものだとご指導を受けました.
まだ実際手を動かしてみていないのですが,また考えてみます.
Re: 背景輻射光子と陽子の衝突
toorisugari no Hiro さんのレス (2009/07/16(Thu) 21:10)
前に挙げた式に置いて
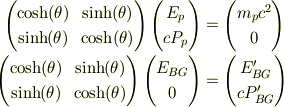
背景輻射を単独の光子と考え,運動量( 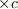 )を
)を
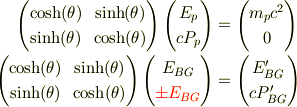
と書き換えれば符号の取り方(光子が逃げるか近づくか)によってmNejiさんの結果と等しくなります. しかし,背景輻射に特定の方向があるとは考えづらいし,今,時空2次元で考えてますが,単独光子なら時空4次元で考えるべきでしょう.
それがあったので,背景輻射を光子気体と考えて平均の運動量は0として,式を立てたのですが,どうもよく分かりません. # 地球が背景輻射に対して静止していないのは承知.
これだと,背景輻射は 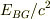 の質量をもつ粒子が散在していることと等しくなってしまう...
の質量をもつ粒子が散在していることと等しくなってしまう...
識者よろしく.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/16(Thu) 21:58)
>背景輻射に特定の方向があるとは考えづらいし,
と思いますが,本問でのプロトンの運動エネルギはとてつもなく巨大なので,その速度は,「実験室系」からみて,光速に限りなく接近しているのですよね.
でも,そんなプロトンでも,光子と衝突するには正面衝突を仮定するのが素直だとおもいます.その意味では時空2次元で十分では?
そして,「実験室系」〜「地球座標系」に対する背景輻射の運動量をゼロと置くのはどうしてでしょうか?
Re: 背景輻射光子と陽子の衝突
toorisugari no Hiro さんのレス (2009/07/16(Thu) 22:54)
実際の計算では余り変わらないでしょうが,背景輻射を気体でなく低エネルギの光子単体と考えてよいか分からないです.
> そして,「実験室系」〜「地球座標系」に対する背景輻射の運動量をゼロと置くのはどうしてでしょうか?
地球は背景輻射に対して約700km/sで運動しているのはCOBE等で分かっていますが,その速度は問題でなく,2.7Kの黒体放射,つまり,光子気体に対する(光子に対するではないです)静止系で考えるのが筋と思ったからです.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/16(Thu) 23:57)
>背景輻射を気体でなく低エネルギの光子単体と考えてよいか分からないです.
あ,私は「背景輻射」というのは門外漢なので発生のメカニズムも知りませんし,まして「気体」との関係があるとは存じないくらいです.でも,そのメカニズムの如何に依らず,超高速荷電粒子との衝突で意味ある現象を起こすのは,外でも無い「光子」ですよね,それも超高速荷電粒子の運動に対して静止するような超高速運動座標系から見た「光子」の一つ一つとの素過程としての衝突と考えるならば,
>地球は背景輻射に対して約700km/sで運動しているのはCOBE等で分かっていますが
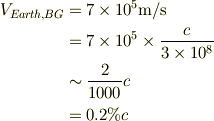
は十分に小さいな速度とも思えます.でも大事なのは,
>その速度は問題でなく,2.7Kの黒体放射,,つまり,光子気体に対する(光子に対するではないです)静止系
これは,そうだと思います.COBE等の解析がどのような仮定を用いているかに依りますね.でも,3K輻射は,電波望遠鏡の初期から問題になったと記憶しているので,当時は地球系の座標として解析しているのかと推測します.
私は,この問題の背景は,宇宙線の上限エネルギがあるとしたらどのようなメカニズムがあるかの作業仮説の内の一つの設問かと感じます.
でも,ここら辺は,この問題をだされた方が,どの様に考えて出題しているかが問われる所と思います.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/17(Fri) 12:02)
詰まる所,私の場合に判らないのは2つに絞られそうです.
(1)相対論的運動学
検索すると大学のサイトで結構解説されているようです.気長に勉強してみたいです.
(2)背景輻射
宇宙論に近い論議は,近寄り難いと思っているのですが,この機会に眺めて見たいと思いますが,初心者向けに良い参考図書などあれば,お教え下さると幸いです.とくに「気体」としての振る舞いがどこから出て来るか興味があります.
Re: 背景輻射光子と陽子の衝突
toorisugari no Hiro さんのレス (2009/07/17(Fri) 12:13)
> とくに「気体」としての振る舞いがどこから出て来るか興味があります.
これは量子統計力学ですね.もろに. # ボーアの仕事は黒体輻射から始まったわけですし.
ただ,相対論的な(量子)気体は分からないので,識者待ちです.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/17(Fri) 12:48)
>ボーアの仕事は黒体輻射
と言われても,容器が判然としない場合,どうやって統計をイメージできるのか,想像の彼方です.
ところで「ボーア」はお父さん(ニールス)のほうですか?
>相対論的な(量子)気体
これでさらに頭が溶けそうです.こういう論議は夏には向かないとか(汗汗).
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/20(Mon) 15:36)
先日,先生がこの問題をローレンツ不変量の関係から説明して下さいました. 先生の説明によると,ローレンツ不変量をS(実験室系)とすると,(c=1の系とした)
S=(E1+E2)^2-(P1+P2)^2 =… =m1^2+m2^2+2E1E2(1-β1β2cosθ)
この計算結果が,なぜか陽子の静止系での光子のエネルギーになるらしいのですが,私は理解できませんでした.このSそのものの意味はあくまでもローレンツ不変量であって,陽子の静止系での光子のエネルギーではないのではないか…?と疑問に思っています.
私の解釈のどこが間違っているのでしょうか?
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/20(Mon) 18:42)
一度,この問題を出来るだけ詳しく書き出される事をお勧めします.
恐らく出題された内容が不確かなので,一体全体何を問われ,なにを回答すべきかが不明確なので,問題を精通されている方々はコメントを控えられているのではないかと推察しています.
他方,私が最近眺めている本(3つのダークマター,村木 綏・著,開成出版,ISBN4-87603-348-X)で,「最高エネルギ宇宙線のスペクトル」で 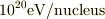 以上にもエラー幅が大きいものの有意分布がある事に驚いている次第です.
以上にもエラー幅が大きいものの有意分布がある事に驚いている次第です.
で,本論に戻りますが,私から見ると,
- 発光源としての2.7°Kの黒体輻射のモデルをどう考えるか.
- 相対論的運動学で,「光子」と「量子」との「質量中心の運動」と「相対の運動」とをどう表現するか.
- 衝突後の反応をどのように考えるか.
を明確にしないといけないように感じます.
私の知識は,これらの疑問に耐えられないので,これにて論議から撤退させていただきます.
Re: 背景輻射光子と陽子の衝突
えり さんのレス (2009/07/20(Mon) 21:12)
>一度,この問題を出来るだけ詳しく書き出される事をお勧めします.
この問題は,大学の宇宙線物理学の授業で出題されました. 最高エネルギー宇宙線の寿命が約一億年だということをこの衝突と絡めてお話したかったのではないかと思います.
「2.7Kの輻射光子は2.3×10^(-4)[eV]に相当し,10^(20)[eV]の陽子の静止系から見ると約100[MeV]となる.陽子と光子によるパイオンの生成断面積は約10^(-28)[cm^2]となるから,約8[Mpc]より遠方からは届かない.」
というコメントが添えられていることと,それから先の議論が最高エネルギー宇宙線の起源がどこなのかという問題になっているため,この問題の焦点は衝突というよりもやはり2.7Kの輻射光子にあると思います..
言葉足らずかもしれませんが,できる限り書いてみました.
Re: 背景輻射光子と陽子の衝突
mNeji さんのレス (2009/07/21(Tue) 00:11)
>この問題の焦点は衝突というよりもやはり2.7Kの輻射光子にあると思います..
という事ならば,このメカニズムに立ち返って勉強するべきだと思います.COBE衛星に加えて,WMAP衛星の詳細データを基にした論議があるようですね.
他方, >2.7Kの輻射光子は2.3×10^(-4)[eV]に相当し,10^(20)[eV]の陽子の静止系から見ると約100[MeV]となる.陽子と光子によるパイオンの生成断面積は約10^(-28)[cm^2]となるから,約8[Mpc]より遠方からは届かない.
を拝見する限り,エネルギが2.3×10^(-4)eVの光子がほぼ均一に分布している中を実験室系で10^(20)eVの陽子,速度Vが通過したとき,パイオンの生成断面積Sは約10^(-28)cm^2を仮定したとして,その反応のQ値,約100MeVを越える相対的運動エネルギがあるかチェックした上で,長さ,L=8Mpcの範囲で十分に衝突が起こる当該光子の数密度を算出し,2.7Kの輻射光子のモデル計算から予測される数密度と比較して論議でもするのでしょうかね.
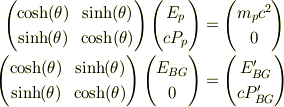
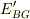 を求める問題でしょうか?それなら
陽子の質量
を求める問題でしょうか?それなら
陽子の質量 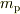 が分かれば計算できますね.
が分かれば計算できますね.