電束密度

しまさんの書込 (2009/07/13(Mon) 21:53)

はじめまして．

大学の編入試験の過去問で自信がないのですが，

xyz空間に置いて，半径a(m)の無限に長い導線がx=0，z=h(m) (h>a) に沿って置かれている．導線上には線電荷密度+Q(C/m)の電荷が存在する． z>0の空間は比誘電率εｒの誘電体で満たされている．

という設定で，

という問題を

導線1(m)の円柱の形に切ったものから電束がQ本出ていると考えて，導線の中心から半径h-zの長さ1(m)の円柱の表面積 π(h-z)^2でQを割ったものすなわち

Q/π(h-z)^2が電束密度と考えたのですが合っていますか？

また (2) (0,0,z)点における電界Eを求めなさいという問題は

真空の誘電率が何も書いてないので求められなくて悩んでました．真空の誘電率を使わないで求められるのでしょうか？

> 表面積π(h-z)^2

これじゃ長さ1(m)の円柱の体積．．．

> 真空の誘電率が何も書いてないので求められなくて悩んでました．

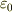$\varepsilon_0$ と置くしかないようですね．

toorisugari no Hiroさん

ありがとうございます！！（２）はそのとおりでした！

（１）はおっちょこちょいなミスでした！！

長さ１ｍの円柱の側面の部分から電束が出ていると考えればいいのかな？

それで，2π(h-z)が表面積なので，電束密度は Q/2π(h-z)となるのですよね？